A circle passe.s through three points A B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle. If angles DAB and CAB are α and β respectively and the distance between the point A and the mid point of the line segment DC is d prove that the area of the circle isπd2cos2α/cos2α + cos2β + 2cosα cos β cosβ - α.
Let the radius of the circle be r. Take x-axis along AC and the O 0 0 as centre of the circle. Therefore coordinate of A and C are - r 0 and r 0 respectively.Now ∠BAC = β ∠BOC = 2βTherefore coordinates of B arer cos 2β r sin 2β.And slope of AD is tan β - α.Let x y be the coordinates of the point D. Equation of AD isTo obtain the coordinate of D solve Eqs. i and ii simultaneouslyTherefore coordinates of D are
Related Solutions
A circle passes through three points A, B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle.If angles DAB and CAB are and respectively and the distance between the point A and the mid-point of the line segment DC is d, prove that the area of the circle is
View SolutionA circle passes through three points A, B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle.If angles DAB and CAB are alpha and beta respectively and the distance between the point A and the mid-point of the line segment DC is d, prove that the area of the circle is (pid^2cos^2a)/(cos^2alpha+cos^2beta+2cosalphacosbetacos(beta-alpha)
View SolutionA circle passes through points A, B and C and AC is its diameter. The line passing through point A intersects the chord BC at point D inside the circle. if angle DAB And CAB respectively alpha And beta and d is the distance between the point A and the mid-point of the line segment DC, then prove that the area of the circle (pid^(2)cos alpha)/(cos^(2)alpha+cos^(2)beta+2 cos alpha cos beta cos (beta-alpha)) Is.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionThe center of the segment AB is C, now two circles are drawn with diameters AC and BC. A straight line passing through point C intersects two circles at points E and F respectively. Now prove that CE = CF.
View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that
View SolutionTwo circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.10.34). Prove that B lies on the line segment DC.
View SolutionTwo circles intersect at two points A and B AD and AC are diameters to the two circles Prove that B lies on the line segment DC.
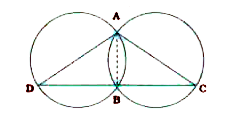
View SolutionTwo circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.10.34). Prove that B lies on the line segment DC.
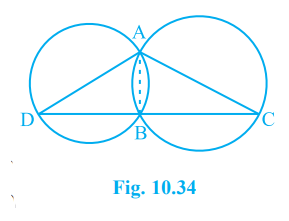
View Solutionदो वृत्त दो बिंदुओं A और B पर प्रतिच्छेद करते है । AD और AC दोनों वृत्तों के व्यास है । सिद्ध कीजिए कि B रेखाखंड DC पर स्थित है ।
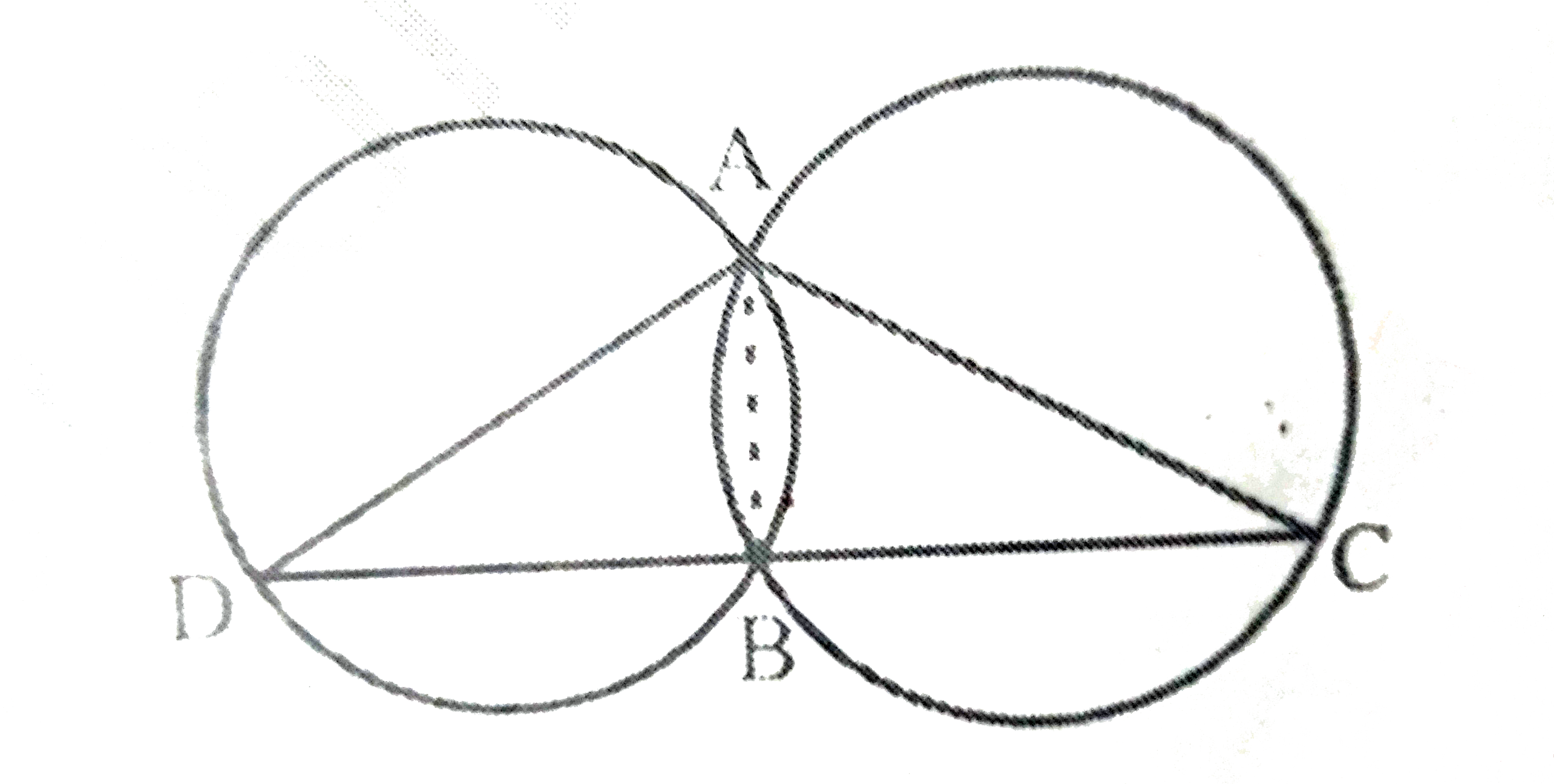
View SolutionTwo circles intersect at two points A and B . AD and AC are diameters to the two circles .Prove that B lies on the line segment DC.

View SolutionA chord of a circle is a line segment with its end points....
View SolutionProve that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
View SolutionIn the center circle O AB is a diameter and AC is a chord. A straight line passing through point O parallel to AC intersects the pressure BC at point D. Prove that BD = CD
View SolutionA secant is a line which intersects the circle at two distinct points and the line segment between the points is a chord.
View SolutionA secant is a line which intersects the circle at two distinct points and the line segment between the points is a chord.
View SolutionAB is a diameter and AC is a chord of the circle with centre at Q. the radius parallel to AC intersect the circle at D. Prove that D is the mid-point of the are BC.
View SolutionThe measure of the line segment joining the centre of a circle to the mid-point of a chord is :
View Solution