If two chords of a circle are equally inclined to the diameter through their point of intersection prove that the chords are equal.
Let AB and AC be two chords and AOD be a diameter such that.
Related Solutions
If two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
View SolutionIf two chords of a circle are equally inclined to the diameter through their point of intersection, prove that the chords are equal.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View SolutionIf two intersecting chords of a circle make equal angles with diameter passing through their point of intersection, prove that the chords are equal.
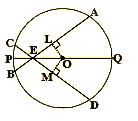
View SolutionIf two intersecting chords of a circle make equal angles with diameter passing through their point of intersection, prove that the chords are equal.
View SolutionIf two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
View SolutionIf two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
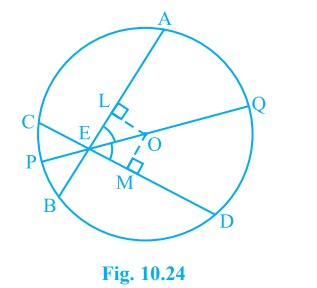
View SolutionIf two chords of a circle have the same inclination with the diameter at the point of intersection, then prove that the chords are equal.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View Solutionयदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं |
View Solutionयदि एक वृत्त की दो प्रतिच्छेदी जीवाएं प्रतिच्छेद बिंदु से जाने वाले व्यास से समान कोण बनाएँ, तो सिध्द कीजिए की वे जीवाएं बराबर है।
View SolutionIf two equal chords of a circle intersect within the circle, prove that
the segments of one chord are equal to corresponding segments
of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
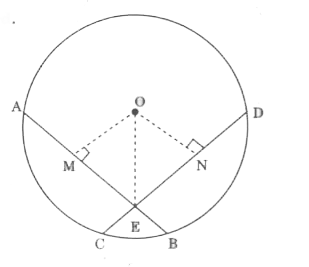
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord.
View Solution