If two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
To prove that the segments of one chord are equal to the corresponding segments of the other chord when two equal chords of a circle intersect within the circle, we will follow these steps:
1. Draw the Circle and Chords:
- Let the circle be centered at point O. Draw two equal chords AB and CD that intersect at point E inside the circle.
2. Label the Segments:
- Let AE = x, EB = y, CE = z, and ED = w. Since AB and CD are equal chords, we have AB = CD.
3. Use the Property of Equal Chords:
- Since AB and CD are equal chords, the perpendicular distances from the center O to the chords are equal. Let OM be the perpendicular distance from O to chord AB, and ON be the perpendicular distance from O to chord CD. Thus, OM = ON.
4. Consider Triangles:
- In triangles OME and ONE, we have:
- OM = ON (as established),
- OE is common to both triangles,
- Angles OME and ONE are both right angles (90 degrees).
- By the Hypotenuse-Leg (HL) theorem, triangles OME and ONE are congruent.
5. Conclude Segment Equality:
- Since triangles OME and ONE are congruent, it follows that:
- ME = NE.
- This means that the segments of the chords are equal:
- AE + ME = CE + NE.
- Thus, we can express this as:
- AE + ME = CE + ME (since ME = NE).
- Therefore, AE = CE and EB = DE.
6. Final Conclusion:
- We have shown that the segments of one chord are equal to the corresponding segments of the other chord:
- AE = DE and EB = CE.
- Let the circle be centered at point O. Draw two equal chords AB and CD that intersect at point E inside the circle.
- Let AE = x, EB = y, CE = z, and ED = w. Since AB and CD are equal chords, we have AB = CD.
- Since AB and CD are equal chords, the perpendicular distances from the center O to the chords are equal. Let OM be the perpendicular distance from O to chord AB, and ON be the perpendicular distance from O to chord CD. Thus, OM = ON.
- In triangles OME and ONE, we have:
- OM = ON (as established),
- OE is common to both triangles,
- Angles OME and ONE are both right angles (90 degrees).
- By the Hypotenuse-Leg (HL) theorem, triangles OME and ONE are congruent.
- Since triangles OME and ONE are congruent, it follows that:
- ME = NE.
- This means that the segments of the chords are equal:
- AE + ME = CE + NE.
- Thus, we can express this as:
- AE + ME = CE + ME (since ME = NE).
- Therefore, AE = CE and EB = DE.
- We have shown that the segments of one chord are equal to the corresponding segments of the other chord:
- AE = DE and EB = CE.
Topper's Solved these Questions
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.5
11 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - Exercise 10.3
3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.1
1 Videos
- CONSTRUCTIONSBOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.2
5 Videos
Similar Questions
If two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionEqual chords of a circle are equidistant from circle.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionEqual chords of a circle are equidistant from the centre.
View SolutionIf two chords of a circle intersect inside or outside the circle when produced ; the rectangle formed by the two segments of one chord is equal in area to the rectangle formed by the two segments of the other chord.
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
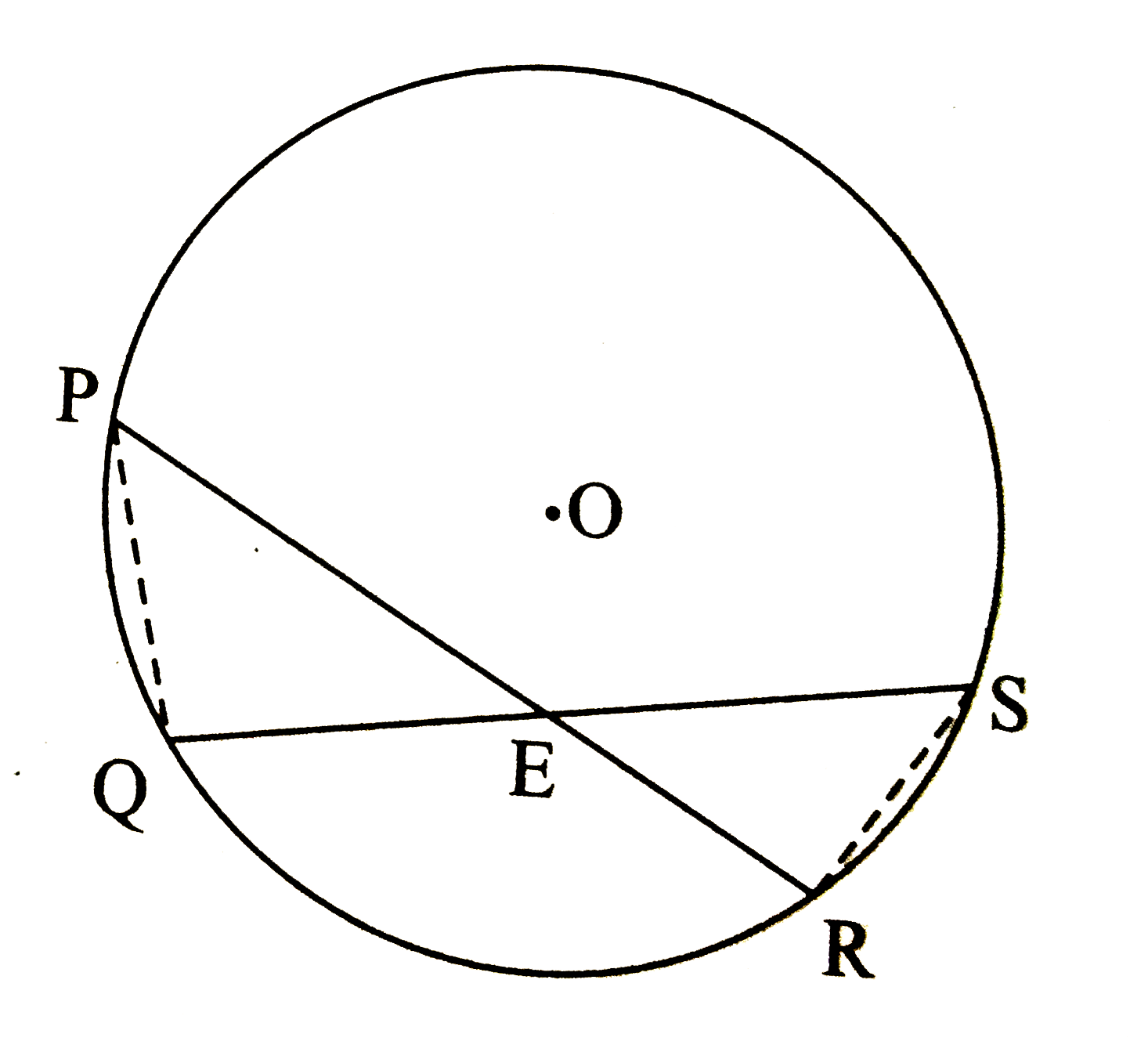
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RS
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionTwo perpendicular chords intersect in a circle.The segments of one chord are 3 and 4, the segments of the other chord are 6 and 2. The diameter of the circle is
View Solution
