The angles of elevation of the top of a tower from two points A and B at distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab.
Let the height of the tower OT = hLet O be the base tower.Let A and B be two points on the same line through the base such thatOA = a OB = b:. The angles at A and B are complementary
Related Solutions
The angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
View SolutionIf the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4m and 9m, find the height of the tower from the base of the tower and in the same straight line with it are complementary.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View Solutionयदि किसी मीनार के आधार से और एक सरल रेखा में a तथा b दूरी पर स्थित दो बिन्दुओं से मीनार के शीर्ष के उन्नयन कोण पूरक हैं, तो मीनार की ऊँचाई हैं :
View SolutionThe angle of elevation of the top of a tower of height "h" metres from two points at a distance of "a" and "b" metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is meters.
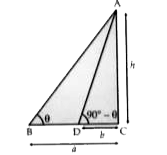
View SolutionThe angles of elevation of the top of a tower from two points at a distances a meter and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is metres.
View SolutionThe angles of elevation of the top of a tower at two points, which are at distances a and b from the foot in the same horizontal line and on the same side of the tower, are complementary. The height of the tower is
View SolutionThe sum of angles of elevation of the top of a tower from two points distance a and b from the base and in the same straight line with it is . Then the height of the tower is :
View SolutionThe angles of elevation of the top of a tower from two points at distances and metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is metres.
View Solutionएक टावर के आधार से जाती हुई एक रेखा पर a और b दूरियों पर स्थित दो बिन्दुओं से टावर की चोटी के उन्नयन कोण एक दूसरे के कोटि पूरक हैं। सिद्ध कीजिए कि टावर की ऊँचाई है।
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angle of elevation of the top of a tower from two points at a distance of 4m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
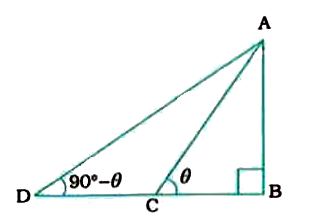
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angle of the elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it, are complementary. Prove that the height of the tower is 6m.
View SolutionFrom the base of a tower and at two points at a distance of 6 the angles of elevation of the top of the tower are complementary to each other. the height of the tower is
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View Solution