Let C1 and C2 be the graphs of functions y = x2 and y = 2x 0 ≤ x ≤ 1 respectively. Let C3 be the graph of a function y = fx 0 ≤ x ≤ 1 f0 = 0. For a point P on C1 let the lines through P parallel to the axes meet C2 and C3 at Q and R respectively see figure. If for every position of Pon C1 the areas of the shaded regions OPQ and ORP are equal determine the function fx.
Refer to the Fig. in the question. Let the coordinates of P be x x2 where 0 ≤ x ≤ 1.For the area OPRO upper boundary y = x2lower boundary : y = fxlower limit of x : 0upper limit of x : x
Related Solutions
Let C_1 and C_2, be the graph of the functions y= x^2 and y= 2x, 0<=x<= 1 respectively. Let C_3, be the graph of a function y- (fx), 0<=x<=1, f(0)=0. For a point Pand C_2, let the lines through P, parallel to the axes, meet C_2 and C_3, at Q and R respectively. If for every position of P (on C_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionLet be the graphs of the functions and respectively, where Let be the graph of a function where For a point on let the lines through parallel to the axis, meet and at and respectively (see Figure). If for every position of the areas of the shaded regions and are equal, determine the function
View SolutionLet be the graphs of the functions and respectively, where Let be the graph of a function where For a point on let the lines through parallel to the axis, meet and at and respectively (see Figure). If for every position of the areas of the shaded regions and are equal, determine the function
View SolutionLet be the graphs of the functions respectively, where be the graph of a function y=f(x), where For a point P on let the lines through P, parallel to the axes, meet at Q and R, respectively (see figure). If for every position of the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
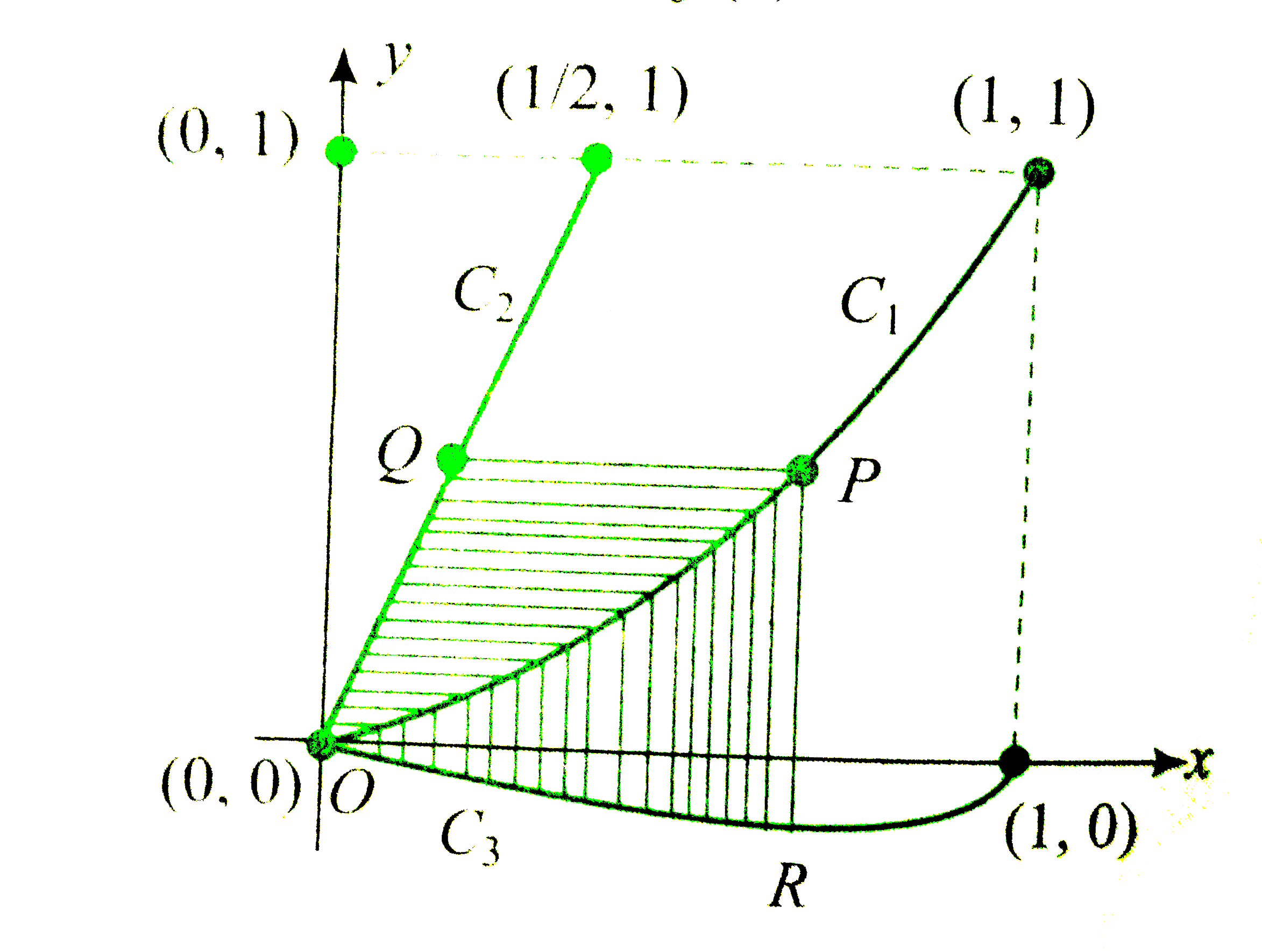
View SolutionLet be the graphs of the functions respectively, where be the graph of a function y=f(x), where For a point P on let the lines through P, parallel to the axes, meet at Q and R, respectively (see figure). If for every position of the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

View SolutionLet be the graphs of the functions respectively, where be the graph of a function y=f(x), where For a point P on let the lines through P, parallel to the axes, meet at Q and R, respectively (see figure). If for every position of the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

View SolutionLet and be two circles whose equations are and and is a variable point . List 1 a) P lies inside C1 but outside C2 2)P lies inside C2 but outside C1 c)P lies outside C1 but outside C2 d)P does not lie inside C2 List 2 p)λ ϵ (−∞,−1)∪(0,∞) q)λ ϵ (−∞,−1)∪(1,∞) r)λ ϵ (−1,0) s)λ ϵ (0,1)
View SolutionLet conditions C1 and C2 be defined as follows: C1: b^2- 4ac > 0, C2: a, -b, c are of same sign. The roots of ax^2+ bx + c = 0 are real and positive, if (a) both C1 and C2 are satisfied (b) only C2 is satisfied (c) only C1 is satisfied (d) None of these
View Solution0.जब C1 और C2 धरिता के संधारित समंतर क्रम में संयोगजीत किए जाते हैंपरिनामी धरिता है (A) C1+C2 (B) C1C2/(C1+C2) (C) (C1+C2)/C1C2 (D)C1/C2
View SolutionFive chairs C1, C2, C3, C4 and C5 are placed one above the other. If C1 is above C2, C3 is above C4 but below C5 and C4 is above C1, which chair is in the middle?
View SolutionThe circle C1 :, with center at O, intersects the parabola at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii and centers Q2 and Q3, respectively.If lies on the y-axis, then
View SolutionThe circle C1 :, with center at O, intersects the parabola at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii and centers Q2 and Q3, respectively.If lies on the y-axis, then find and
View SolutionThe circle C1 :, with center at O, intersects the parabola at the point P in the first quadrant. Let the tangent to the circle C1 at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii and centers Q2 and Q3, respectively.If lies on the y-axis, then
View SolutionConsider two curves C1:y^2=4x ; C2=x^2+y^2-6x+1=0 . Then,
View SolutionLet be distinct positive numbers. Three lines and are concurrent, if
View SolutionConsider two curves ; . Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
View SolutionConsider two curves C1:y^2=4x; C2=x^2+y^2-6x+1=0. Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
View SolutionConsider two curves C1:y^2=4x ; C2=x^2+y^2-6x+1=0 . Then, (a) C1 and C2 touch each other at one point (b) C1 and C2 touch each other exactly at two point (c) C1 and C2 intersect(but do not touch) at exactly two point (d) C1 and C2 neither intersect nor touch each other
View SolutionConsider two curves C1:y^2=4x ; C2=x^2+y^2-6x+1=0 . Then, a. C1 and C2 touch each other at one point b. C1 and C2 touch each other exactly at two point c. C1 and C2 intersect(but do not touch) at exactly two point d. C1 and C2 neither intersect nor touch each other
View Solutionमाना और क्रमशः फलन और के ग्राफ हैं। माना फलन, का ग्राफ है। के एक बिंदु P के लिए माना कि बिन्दु P से होकर जाने वाली तथा अक्षों के समान्तर रेखायें व को क्रमशः Q और R पर मिलती है।
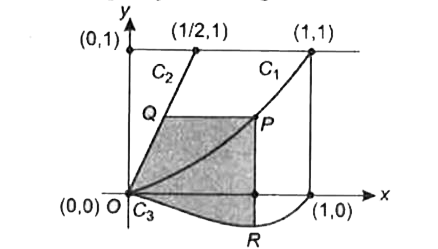 यदिP की प्रत्येक स्थिति ( पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन को ज्ञात कीजिए।
यदिP की प्रत्येक स्थिति ( पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन को ज्ञात कीजिए।
View Solution