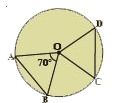
In the given figure O is the centre of the circle ∠BAD = 75° and chord BC = chord CD Find : i ∠BOC ii ∠OBD iii ∠BCD.
i Given ∠BAD = 75° and chord BC = chord CD∠BOD = 2. ∠BAD Angle at the centre is twice the angle at the remaining part of the circle
Related Solutions
In circle is diameter with centre of circle and are equal chord then angle suntened by chord BC at centre is
View Solution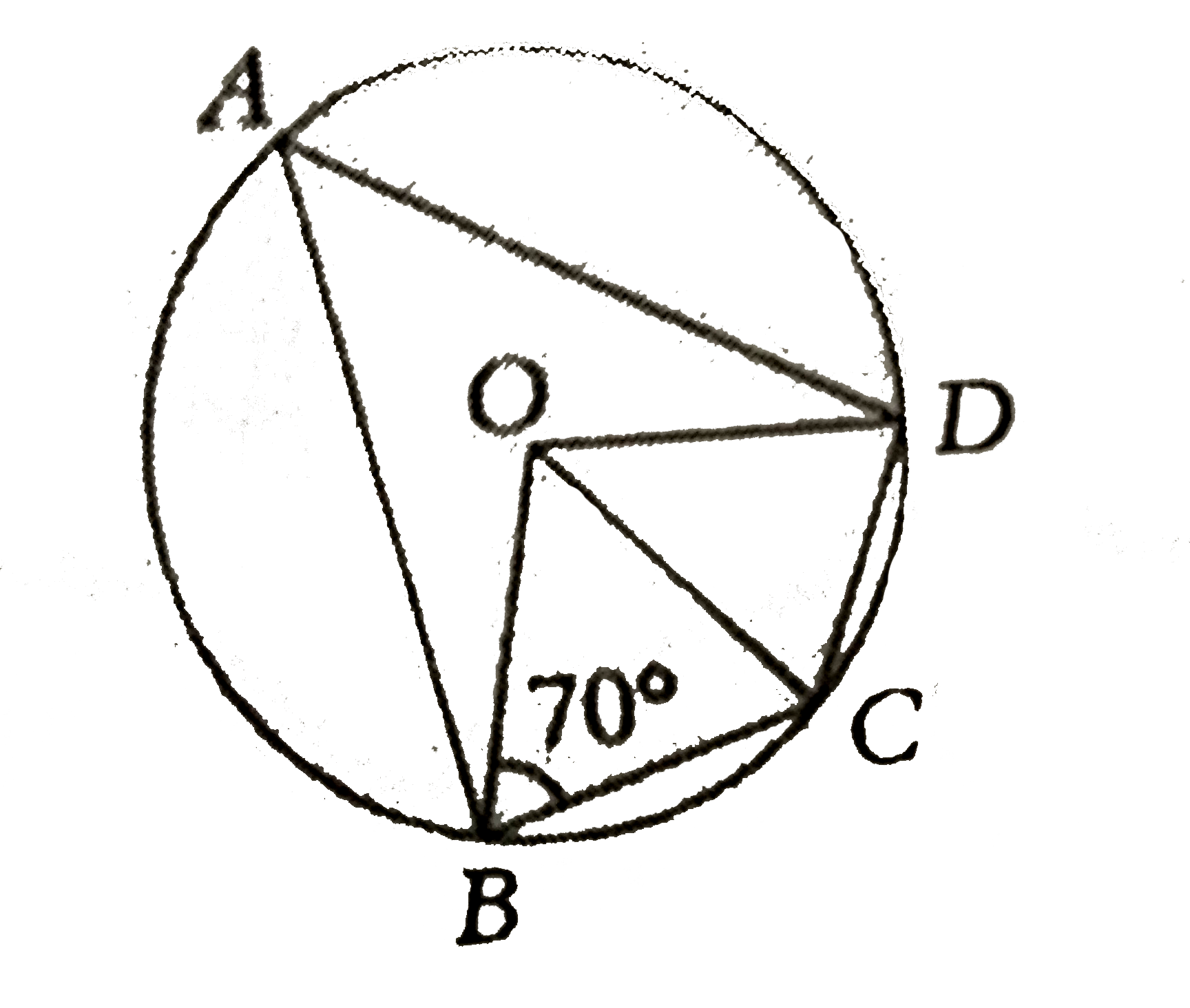
In the above figure (not to scale), O is the centre of the circle. and are equal chords. If , then find .
View Solution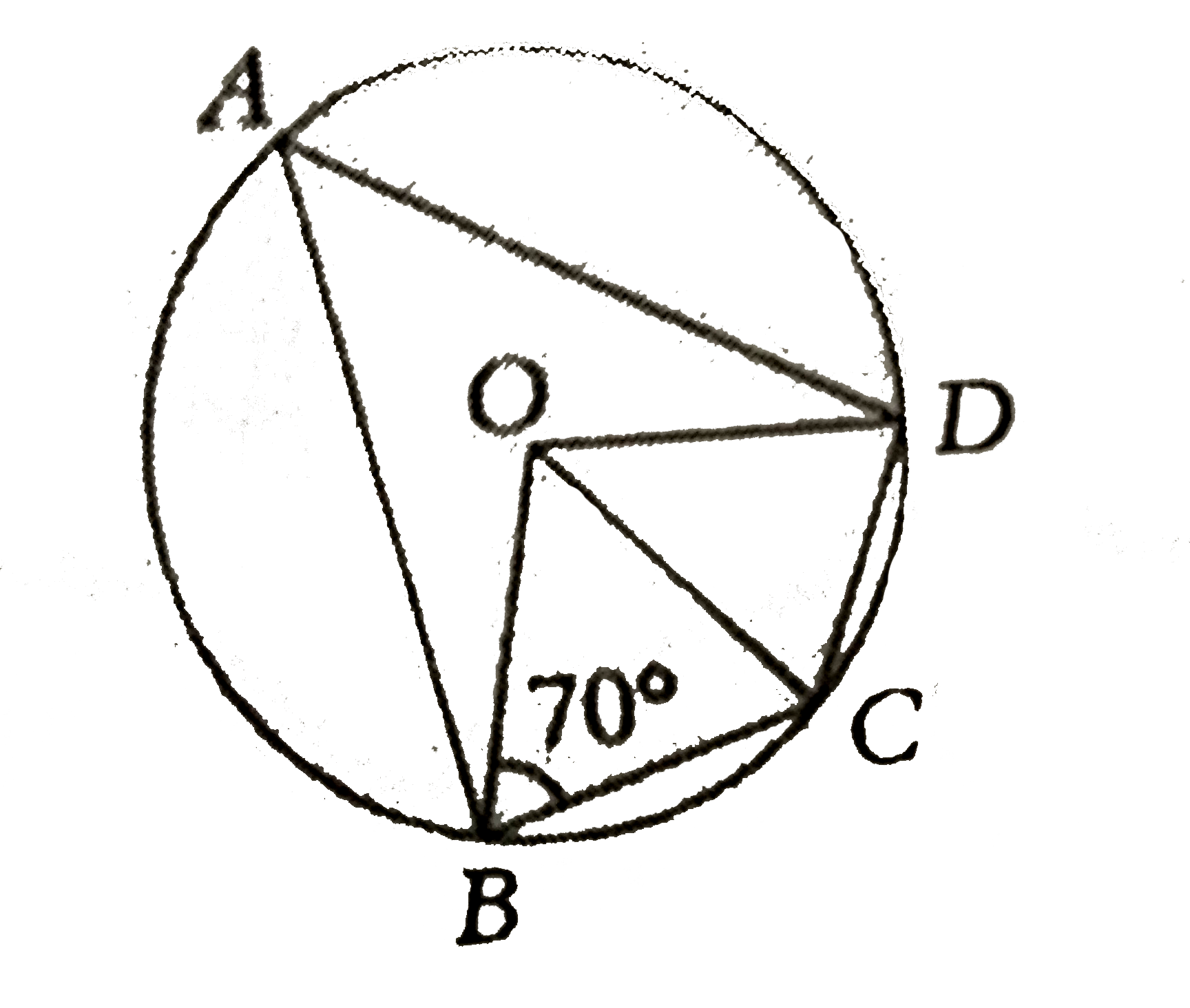
In the above figure (not to scale), O is the centre of the circle. and are equal chords. If , then find .
View SolutionIn the given 'O' is the centre of the circle, Arc find:
View Solution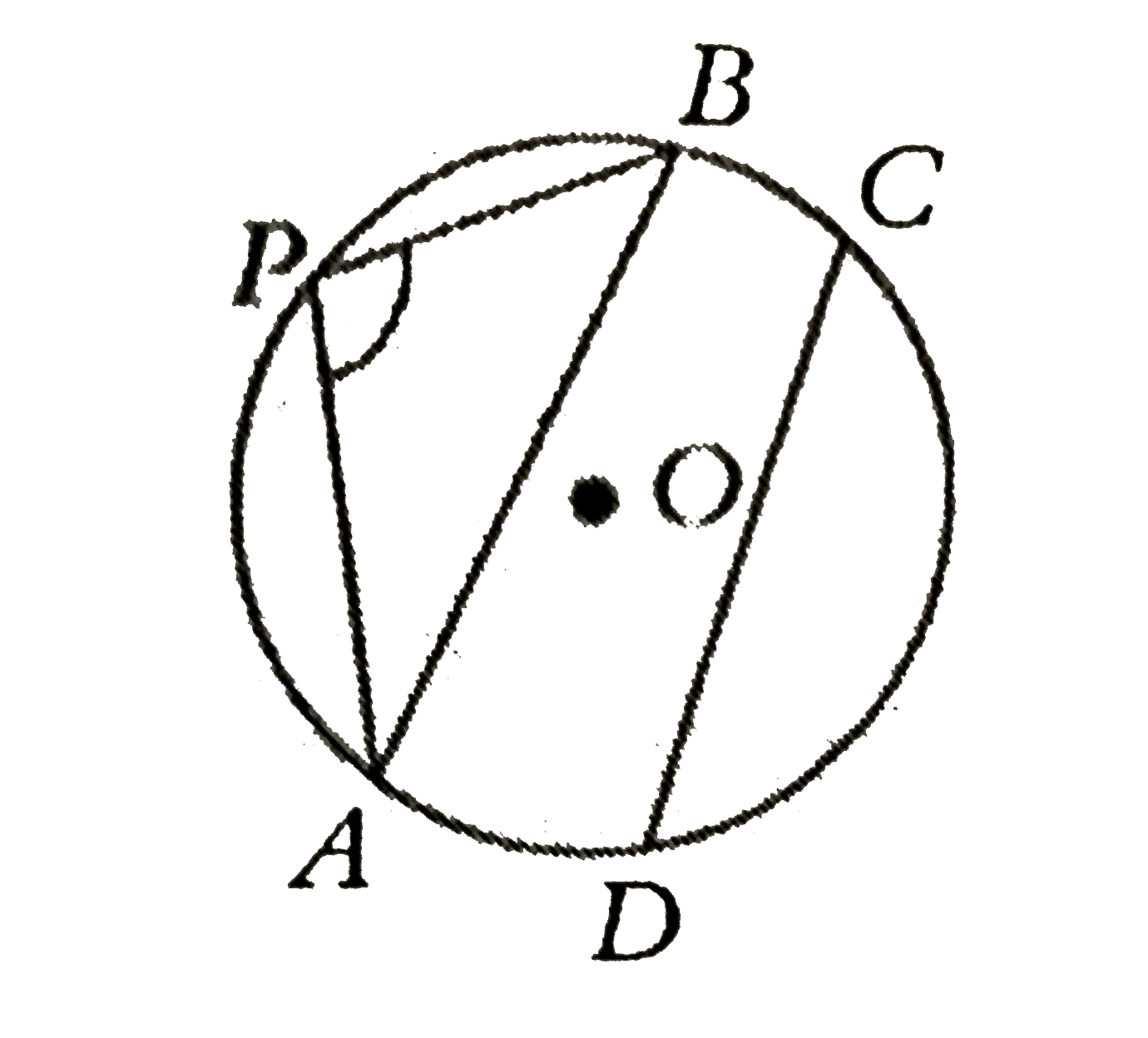
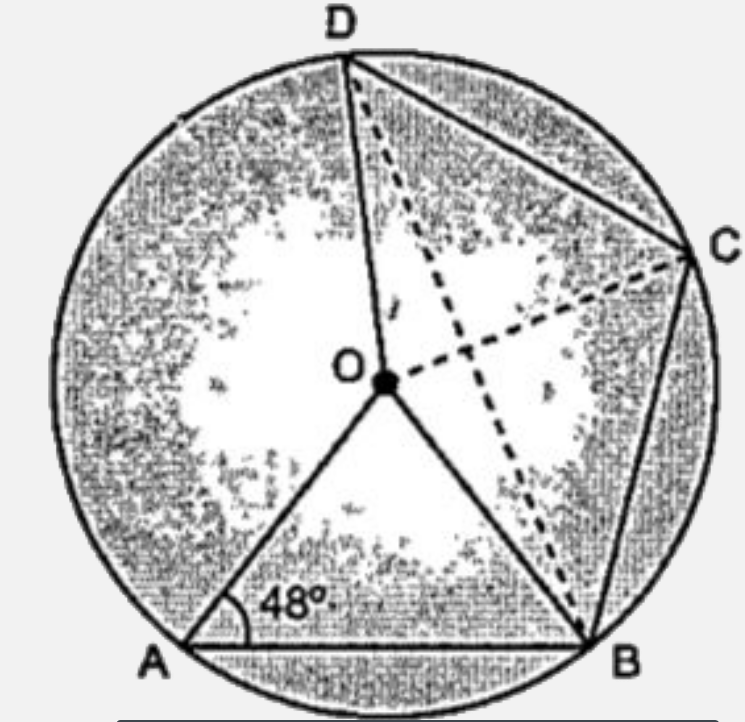
In the above figure, O is the centre of the circle and . If , then find the angle made by the chord CD at the centre.
View Solution
In the above figure, O is the centre of the circle and . If , then find the angle made by the chord CD at the centre.
View SolutionIn the figure given , O is the centre of the circle . , Find the giving suitable reasons , the measure of
(i)
(ii)
(iii)
View SolutionIn the given figure ‘O’ is the centre of the circle and AB, CD are equal chords. If . Find the angles of the OCD
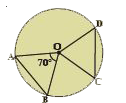
View SolutionIn the given figure ‘O’ is the centre of the circle and AB, CD are equal chords. If . Find the angles of the OCD
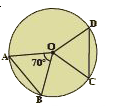
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , , then find .
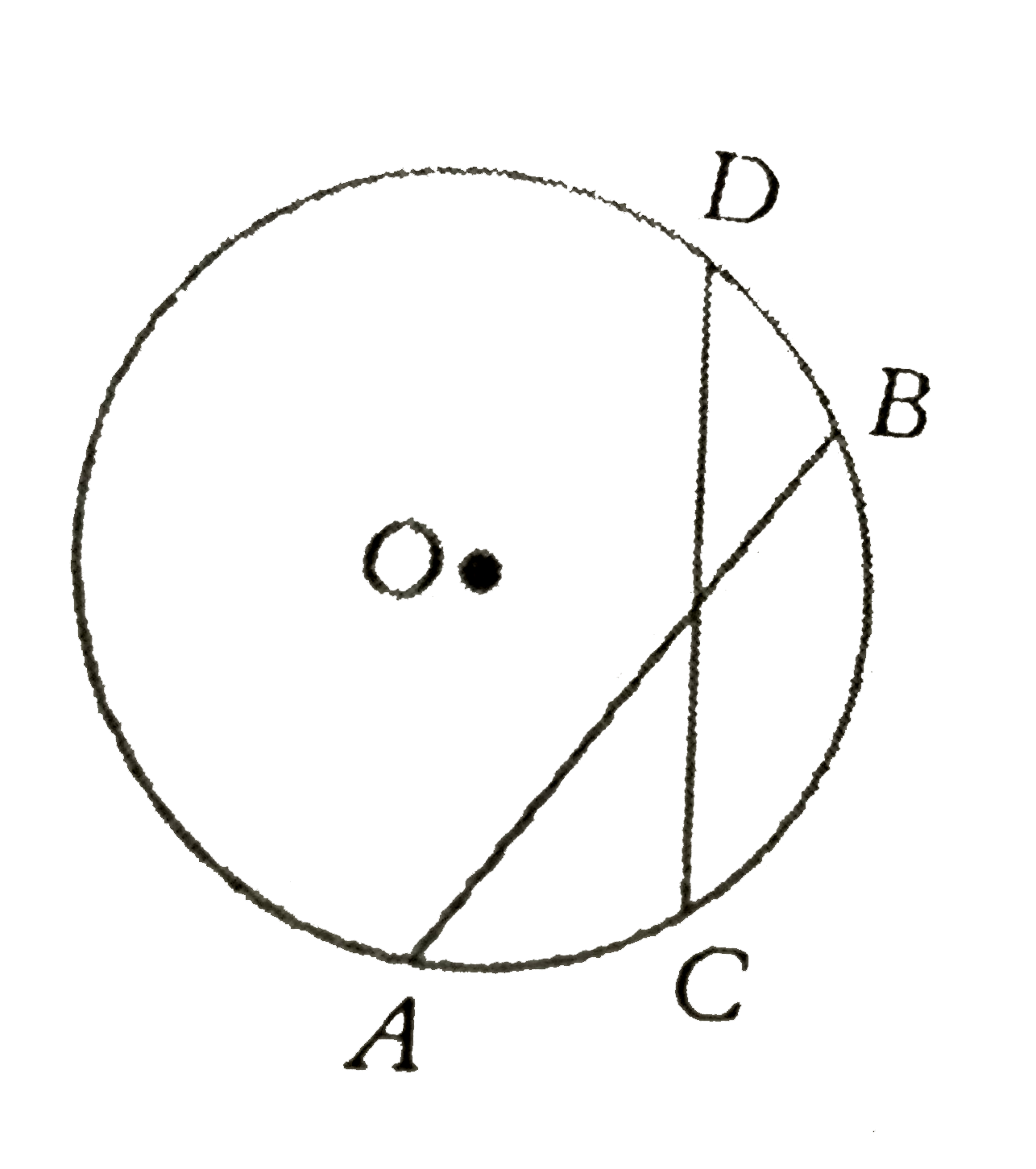
View SolutionIn the given figure ‘O’ is the centre of the circle and AB, CD are equal chords. If . Find the angles of the OCD
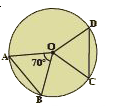
View SolutionIn the given figure ‘O’ is the centre of the circle and AB, CD are equal chords. If . Find the angles of the OCD
View SolutionIn the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and find angleAPQ
View SolutionIn a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is and the length of CD and BC is equal, then find the DBC.
View SolutionIn the figure (i) given below, O is the centre of the circle. AB and CD are the chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB=24 cm OM=5 cm, ON=12 cm. Find the, (i) radius of the circle (ii) length of chord CD (ii) In the figure (ii) given below, CD is diameter which meets the chord AB at E such that AE = BE = 4 cm.If CE = 3 cm, find the radius of the circle.
View SolutionIn circle with centre , if and are equal chords and then angle subtend by chord at = ?
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
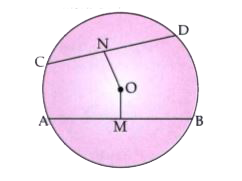
View SolutionIn the given figure, O is the centre of the circle.

Name all chords of the circle.
View SolutionIn the given figure, O is the centre of the circle.

Name a chord, which is not the diameter of the circle.
View SolutionIn given figure, O is the centre of the circle. A chord, which is not the diameter of the circle is
View Solution