In a ΔABC AB = BC = CA = 2a and AD⟂ BC. Prove thati AD =a√3 ii area ΔABC = √3a2
i Here AD⟂ BC.Clearly ΔABC is an equilateral triangle.Thus in ΔABD and ΔACDAD = AD [Common]
Related Solutions
In a and . Prove that (ii) Area
View SolutionΔABC is isosceles with AB=AC=7cm and BC=9cm. The height AD from A to BC, is 6cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
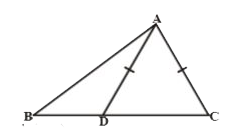
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
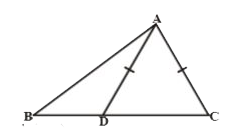
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
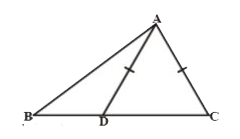
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
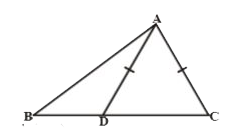
View SolutionIn ΔABC, AB = 4 and BC = 7, Then , .... holds good.
View SolutionIn ΔABC, AB = 6 cm and DE || BC such that AE = 1/4 AC then the length of AD is
View SolutionGiven that ΔABC∼ΔDEF,BC=3cm,EF=4cm ans the area of ΔABC is 54sq.cm.Then find the area of ΔDEF.
View Solutionमें , AB=BC =CA=2a और हैं , तो सिद्ध कीजिए कि |
View SolutionThe incircle of ΔABC touches the sides, AB, BC and AC in the point P, Q and R respectively. If AP=7cm, BC=13cm, find the perimeter of ΔABC.
View SolutionD, E and F are respectively the mid-points of the sides AB, BC and CA of a ΔABC. Prove that by joining these mid-points D, E and F, the ΔABC is divided into four congruent triangles
View SolutionΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is
View SolutionIn figure ΔABC is circumscribing a circle. Find the length of BC
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionIf ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is
View SolutionProve that E is a point E but V (ABE) = V (ACE) on the AD equation of ΔABC in Figure 11.23?
View SolutionIn an ABC, the medians AD, BE and CF intersect at the point. prove that 4 (AD + BE + CF) gt 3 ( AB + BC + CA)
View SolutionD is the midpoint of side BC of ΔABC. Point E lies on AC such that CE = AC/3. BE and AD intersect at G. What is AG/GD?
View SolutionIn Fig. (ii), AD = BC and AD || BC. IS AB = DC? Give reasons in support of your answer.Hint. Prove that .
View Solution