Prove that In equal circles or in the same circle if two chords are equal they cut off equal arcs.
Data:In equal circles AXB and CYD with centres P and Q chord AB = chord CD.To Prove:arc AMB = arc CND; arc AXB = arc CYDProof:
Related Solutions
एक ही वृत्त में बराबर जीवाओं द्वारा काटे गए चाप होते हैं-
View SolutionTheorem:-1If two arcs of a circle are congruent ; the corresponding chord are equal and Equal chords of a circle substends equal angles at the centre.
View Solutionयदि सर्वांगसम वृत्तों में दो चाप बराबर हो, तो उनकी संगत जीवाएँ होगी ।
View SolutionIf two chords of a congruent circle are equal; then their corresponding arcs are also equal.
View SolutionIf two arcs in congruent circles are equal, then their corresponding chords will be
View Solutionयदि सर्वांगसम वृत्तों में दो चाप बराबर हों, तो उनकी संगत जीवाएँ होंगी
View SolutionIf two arcs of a circle are congruent; then corresponding chords are equal
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, then Prove chords are equal.
View Solutionयदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं |
View SolutionThe radius of a circle is 9cm. Find the length of an arc of the ciircle which cuts off a chord of length equal to radius.
View SolutionRecall that two circles are congruent, if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres
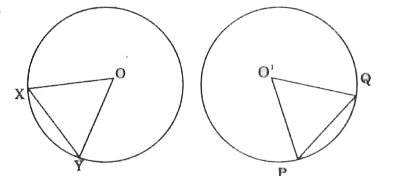
View SolutionRecall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
View SolutionIf two equal chords of a circle intersect within the circle, prove that
the segments of one chord are equal to corresponding segments
of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments ofone chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
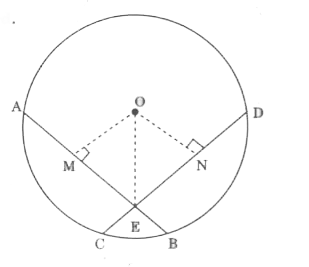
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
View Solution