A beam of light from a light source on the bottom of a swimming pool 3.0 meters deep strikes the surface of the water 2.0 meters to the left of the light source as shown above. The index of refraction of the water in the pool is 1.33.a. What angle does the reflected ray make with the normal to the surface?b. What angle does the emerging ray make with the normal to the surface?c. What is the minimum depth of water for which the light that strikes the surface of the water 2.0 meters to the left of the light source will be refracted into the air?In one section of the pool there is a thin film of oil on the surface of the water. The thickness of the film is 1.0 x 10–7 meter and the index of refraction of the oil is 1.5. The light source is now held in the air and illuminates the film at normal incidence as shown above.d. At which of the interfaces air-oil and oil-water if either does the light undergo a 180° phase change upon reflection?e. For what wavelengths in the visible spectrum will the intensity be a maximum in the reflected beam?
a The reflected angle is the same as the angle of incidence which can be found using the geometry. tan θ = o/a = 2/3 … θ = 34°.b ni sin θi = nr sin θr … 1.33 sin 34° = 1 θr … θr = 48°.c We need to find the critical angle first … ni sin θc = nr sin 90 … 1.33 sin θc = 1 … θc = 49°.Keeping the light source at the same horizontal distance away 2m we have to raise up the light source decreasing the 3m depth until the we reach a point where the new depth and the 2m horizontal side of that triangle reach a 49° angleUsing geometry. Tan θ = o/a tan49 = 2/ ynew → ynew = 1.8 md Light travels from less n to more n to less n. A 180° ½ λ phase shift will happen at the air–oil boundary only.e Based on the ½ λ phase shift air–oil we need to create and additional ½ λ or 1½ λ or 2 ½ λ … phase shift from traveling in the oil to create maximum constructive intensities. To do this oil thicknesses of t = 1/4 λoil 3/4 λoil 5/4 λoil … can be used. For an oil thickness of 100 nm as given these correspond to wavelength in the oil of 400 nm 133.33 nm 80 nm …Now we have to convert these oil wavelengths to air wavelengths using n1 λ1 = n2 λ2 … nair λair = nfilm λfilm … 1 λair = 1.5400 … λair = 600 nm. … repeating for the other λ’s and we get possible air wavelengths of: 600 nm 200 nm 120 nm …Since the visible spectrum in air ranges between 400–700 nm only the 600 nm λ qualifies.
Related Solutions
At what angle must a beam of light on the surface of water , which has an index of refraction of 1.33 for the given light, so that the reflect light may be plane polarized?
View SolutionA ray of light incident normally on a refracting surface of the prism is totally reflected from the other refracting surface. If the prism is immersed in water how will the ray act? Refractive index of glass = 1.5, refractive index of water = 1.33.
View SolutionThe refractive index of water relative to air is 5/3. A ray of light passing from water into air is incident at the interface at an angle of with the normal. What angle does the refreacted ray make with the normal?
View SolutionThe refractive index of water relative to air is 5/3. A ray of light passing from water into air is incident at the interface at an angle of 32^(@) with the normal. What angle does the refreacted ray make with the normal?
View SolutionA vertical ray of light strikes the horizontal surface of some water:
a) What is the angle of incidence?
b) What is the angle of refraction?
View SolutionA plane mirror PQ is help normally to water surface of refractive idex 1.33. A ray of light is incident at an angle of with the nirror surface. After reflection the ray is refracted into water. The angle of refraction r is
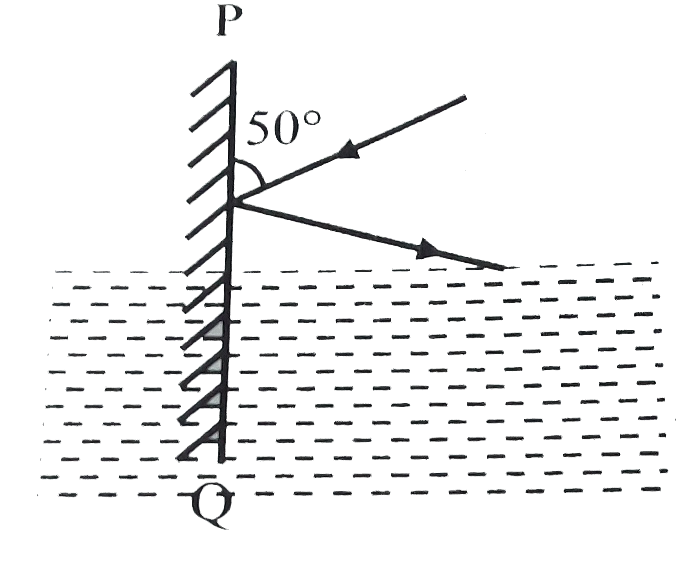
View SolutionA plane mirror PQ is help normally to water surface of refractive idex 1.33. A ray of light is incident at an angle of 50^@ with the nirror surface. After reflection the ray is refracted into water. The angle of refraction r is
View SolutionA ray of light is incident on a glass slab at an angle of 30°. A ray emerging from the other surface of the slab will make an angle with the normal
View SolutionIf a ray of light strikes the surface of mirror at angle of . What will be the angle of reflection.
View SolutionA beam of light is partially reflected and partially refracted from a surface. The angle between reflected and refracted light ray is . If the angle of refraction is , the angle of incidence is
View SolutionA beam of light is partially reflected and partially refracted from a surface. The angle between reflected and refracted light ray is . If the angle of refraction is , the angle of incidence is
View SolutionA beam of light is partially reflected and partially refracted from a surface. The angle between reflected and refracted light ray is . If the angle of refraction is , the angle of incidence is
View Solutionएक तेल की पतली पानी पर तैर रही है। एक प्रकाश किरण के आपतन कोण पर तेल की सतह पर आपतित होती है । किरण द्वारा पानी के अंदर बने अपवर्तन कोण का मान होगा (तेल का अपवर्तनांक = 1.45, पानी का अपवर्तनांक = 1.33)
View SolutionA thin layer of oil is floating on water. a beam of light 45^@ is incident on the surface of the oil at an angle of incidence of The angle of refraction made by the ray inside water will be (refractive index of oil = 1.45, refractive index of water = 1.33)
View Solutionएक तेल की पतली परत पानी पर तैर रही है। एक प्रकाश किरण के आपतन कोण पर तेल को सतह पर आपतित होती है। किरण द्वारा पानी के अन्दर बने अपवर्तन कोण का मान होगा (तेल का अपवर्तनांक पानी का अपवर्तनांक )
View SolutionIf a ray of light incident on an opaque surface makes an angle of 30^@ with the mirror, what will be the angle of reflection of its corresponding reflected ray?
View Solutionपानी की सतह के 4 मीटर नीचे एक प्रकाश स्त्रोत रखा जाता है। पानी का अपवर्तनांक 5/3 है। पानी की सतह पर जो प्रकाश डिस्क बनेगी उसका व्यास होगा
View SolutionA thin layer of oil is floating on water. a ray of light 45^(@) is incident on the surface of the oil at an angle of incidence of The angle of refraction made by the ray inside water is: (refractive index of oil - 1.45 and refractive index of water = 1.33)
View Solutionએક સમતલ પરાવર્તક સપાટી ઉપર A તરંગલંબાઈનો પ્રકાશ આપાત થાય છે. પરાવર્તિત પ્રકાશની તરંગલંબાઈ અને આવૃત્તિ કેટલી હશે? કયા આપાતકોણે, પરાવર્તિત કિરણ એ આપાતકિરણને લંબ હશે?
View SolutionLight rays from a source are incident on a glass prism of index of refraction and angle of prism At near normal incidence, the angle of deviation of the emerging rays is
View Solution