In a uniform magnetic field B directed vertically downward a metal bar of mass m is released from rest and slides without friction down a track inclined at an angle θ as shown. The electrical resistance of the bar between its two points of contact with the track is R. The track has negligible resistance. The width of the track is L.a. Show on the diagram the direction of the current in the sliding bar.b. Denoting by v the instantaneous speed with which the bar is sliding down the incline determine an expression for the magnitude of the current in the bar.c. Determine an expression for the force exerted on the bar by the magnetic field and state the direction of that force.d. Determine an expression for the terminal velocity of the sliding bar.
a The rod forms a loop with the upper part of the rails. Based on Lenz law as the rod slides down the perpendicular component of B increases the flux in the loop and current flows to create a field in the outward normal direction to the rails to counteract the flux change. Using the RHR solenoid the current would flow towards the right side of the bar pictured.b The induced emf in the bar is given by ε = Blv ⊥ . The perpendicular B is given with B cos θ similar to Fgx so the induced emf is BLv cos θ. With V = IR … This gives IR = BLv cos θ and the current is I = BLv cos θ / Rc F = BIL ⊥ again using B cos θ we have Fb = B cos θ I L now sub in I from above. Fb = B cos θBLv cos θ / RL Fb = B2L2v cos2 θ / R. Based on the RHR for the bar the force acts up the inclined rails parallel to them.d The terminal velocity will occur when Fnetx = 0 with x being the direction along the rails. This gives:Fgx = Fb mg sin θ = B2L2v cos2 θ / R v = mg sin θ R / B2L2 cos2 θ
Related Solutions
लम्बवत् वलय की त्रिज्या r तथा प्रतिरोध R है, यह लम्बवत् गिरती है। यह दो लम्बवत् पटरियों (rail) के सम्पर्क में रखी है, जो सिरों पर जुड़ी हैं। चित्र में दिखाया गया है। पटरियों में कोई घर्षण तथा प्रतिरोध नहीं है। यहाँ एक समान क्षैतिज चुम्बकीय क्षेत्र का परिमाण B वलय तथा पटरी के तल के लम्बवत् है। जब वलय का वेग v है, तो PQ भाग में धारा है

View SolutionA small roller coaster starts at point A with a speed u on a curved track as shown in the figure The friction between the roller coaster and the track is negligible and it always remains in contact with the track. The speed of roller coaster at point D on the track will be
View SolutionA small roller coaster starts at point A with a speed u on a curved track as shown in the figure The friction between the roller coaster and the track is negligible and it always remains in contact with the track. The speed of roller coaster at point D on the track will be
View SolutionA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View SolutionA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View SolutionA small object of mass m starts from rest at the position shown and slides along the fricationless loop-the -loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View SolutionA small of mass m starts from rest at the position shown and slides along the frictionless loop the loop track of radius R. What is the smallest value of y such that the object will slide without losing contact with the track?
View SolutionIn the figure shown, a small ball of mass 'm' can move without sliding in a fixed cylindrical track of radius R in vertical plane. It is released from the top. The resultant force on the ball at the lowest point of the track is
View SolutionA block of mass M, with a semicircular track of radius R rest on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest at the point of the semicircular track. The cylinder slips in the semicircular frictionless track. How far the block moved when the cylinder reaches the bottom of the track ?
View SolutionA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m , are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
View SolutionA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m , are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
View SolutionAs shown in the figure, a small is released from a certain height which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
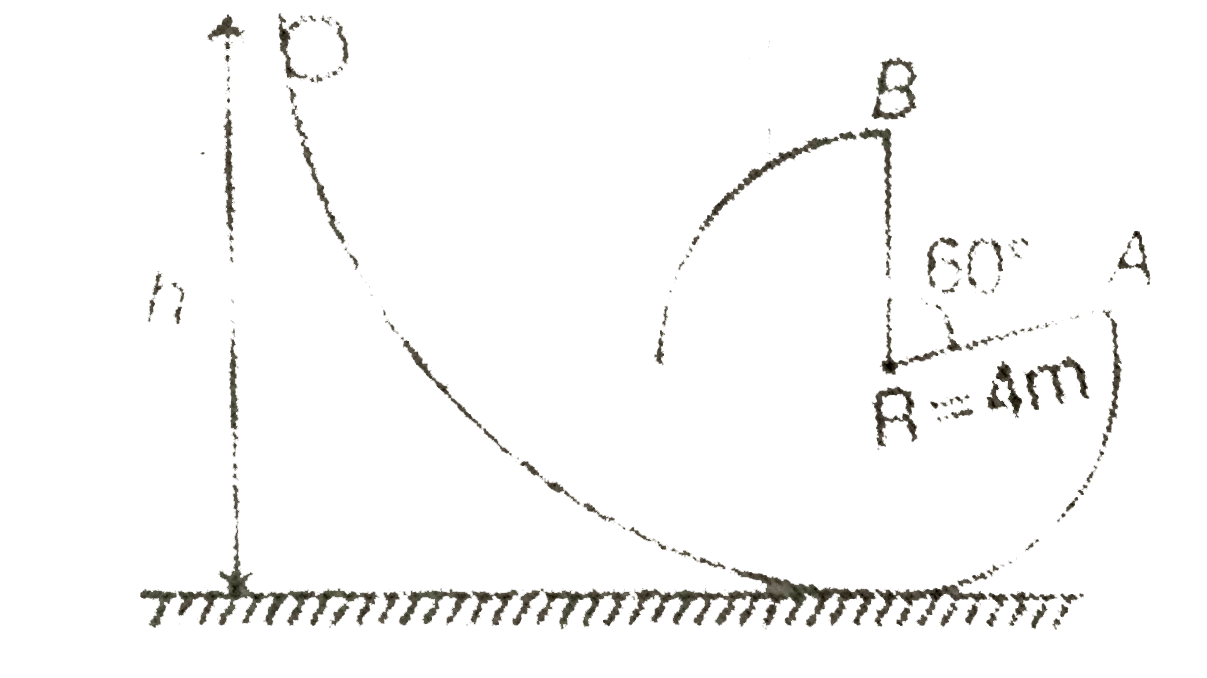
View SolutionAs shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
View SolutionIn the figure a charged small sphere of mass and the charge starts sliding from rest on a vertical fixed circular smooth track of radius from the position shown. There exist a uniform magnetic field of . Find the maximum force exerted by track on the sphere during its motion.
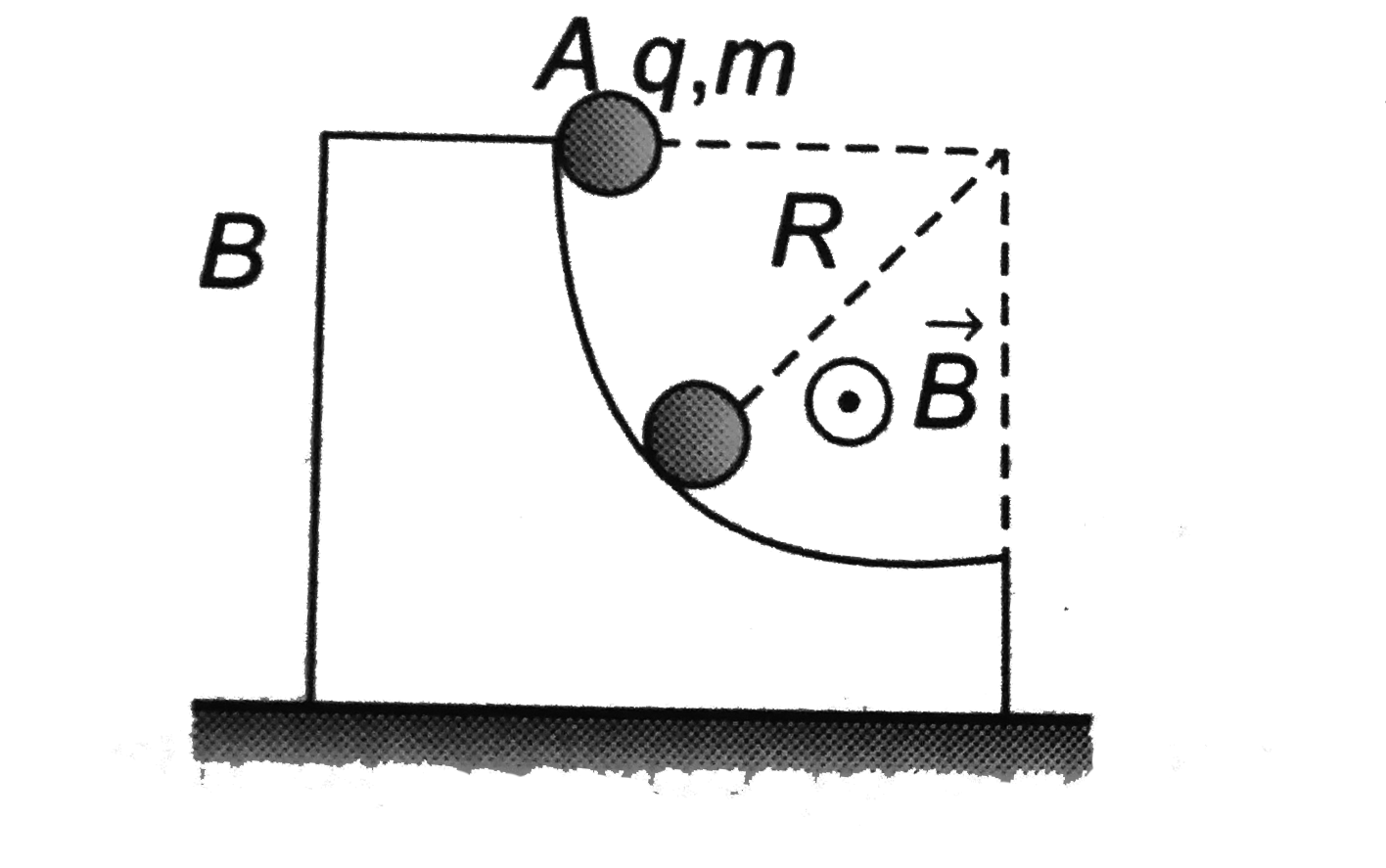
View SolutionIn the figure a charged small sphere of mass and the charge starts sliding from rest on a vertical fixed circular smooth track of radius from the position shown. There exist a uniform magnetic field of . Find the maximum force exerted by track on the sphere during its motion.

View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed . Calculate the angle with respect o the vertical where it leaves contact with the track.
View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed .Calculate the angle with respect to the vertical where it leaves contact with the track .
View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed v_0 . calculate the angle theta with respect to the vertical where it leaves contact with the track.
View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed v_(theta) . Calculate the angle theta with respect to the vertical where it leaves contact with the track.
View Solution