A metal rod of mass 0.22 kg lies across two parallel conducting rails that are a distance of 0.52 m apart on a tabletop as shown in the top view. A 3.0 Ω resistor is connected across the left ends of the rails. The rod and rails have negligible resistance but significant friction with a coefficient of kinetic friction of 0.20. There is a magnetic field of 0.80 T perpendicular to the plane of the tabletop. A string pulls the metal rod to the right with a constant speed of 1.8 m/s.a Calculate the magnitude of the current induced in the loop formed by the rod the rails and the resistor and state its direction.b Calculate the magnitude of the force required to pull the rod to the right with constant speed.c Calculate the energy dissipated in the resistor in 2.0 s.d Calculate the work done by the string pulling the rod in 2.0 s.e Compare your answers to parts c and d. Provide a physical explanation for why they are equal or unequal.
a Combine induced emf ε = Blv with V = IR …IR = Blv … I3 = 0.80.521.8 … I3 = 0.749 I = 0.25 A Based on lenz law for the loop formed by the rod resistor and rails flux is gained into the page as the rod moves so current is generated to add field out of the page to counteract the flux change. Using the RHR solenoid for lenz law the current would flow CCW and up the rod.b Using the RHR for the rod the magnetic force acts left. In addition there is friction. So the FBD has the string force to the right and friction + magnetic force to the left. Fnet = 0 … Fpull – Fb –fk = 0 …Fpull = μkmg + BIL = 0.20.229.8 + 0.80.250.52 = 0.535 Nc W = IVt = 0.250.752 = 0.374 Jd moving at 1.8 m/s for 2 seconds. v = d/t the string moves 3.6 m. W = Fd = 0.5353.6 = 1.93 Je The work of the string is more because it has to provide the energy to the resistor and work against friction also.
Related Solutions
Passage
A metal rod of mass mrests on two horizontal rails distance apart. It carries a current i from one rail to the other. The coefficient of static friction between the rod and the rails is
If a magnetic field is applied, the angle with the horizontal of the minimum magnetic force on the rod which puts the rod on the verge of sliding is
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then
View SolutionPassage
A metal rod of mass mrests on two horizontal rails distance apart. It carries a current i from one rail to the other. The coefficient of static friction between the rod and the rails is
The magnitude of the minimum magnetic field which puts the rod on the verge of sliding is
View SolutionPassage
A metal rod of mass mrests on two horizontal rails distance apart. It carries a current i from one rail to the other. The coefficient of static friction between the rod and the rails is
The angle with the vertical of the minimum magnetic field which puts the rod on the verge of sliding is
View SolutionA pair of long, smooth, parallel, horizontal, conducting rails are joined to a cell at one end. There are no external electric or magnetic fields. A metal rod is placed on the rails. The rod will
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is mu_(s) What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View Solutionएक कॉपर की छड़ का द्रव्यमान m है। यह दो क्षैतिज समान्तर चिकनी पटरियों (rails) जिनके बीच की दूरी । है तथा क्षैतिज के साथ कोण बनाती है, पर गुरुत्व के अन्तर्गत फिसलती है। तली में पटरियाँ एक प्रतिरोध R के द्वारा चित्रानुसार जुड़ी हैं। यहाँ एकसमान चुम्बकीय क्षेत्र B पटरियों (rails) के तल के लम्बवत् है। छड़ का क्रान्तिक वेग है

View SolutionTwo parallel rails with negligible resistance are apart. The are connected by a resistor. The circuit also contains two metal rods having resistances of and along the rails. The rods are pulled away from the resistor at constant speeds and respectively. A uniform magnetic field of magnitude is applied perpendicular to the, plane of the rails. Determine the current in the resistor.
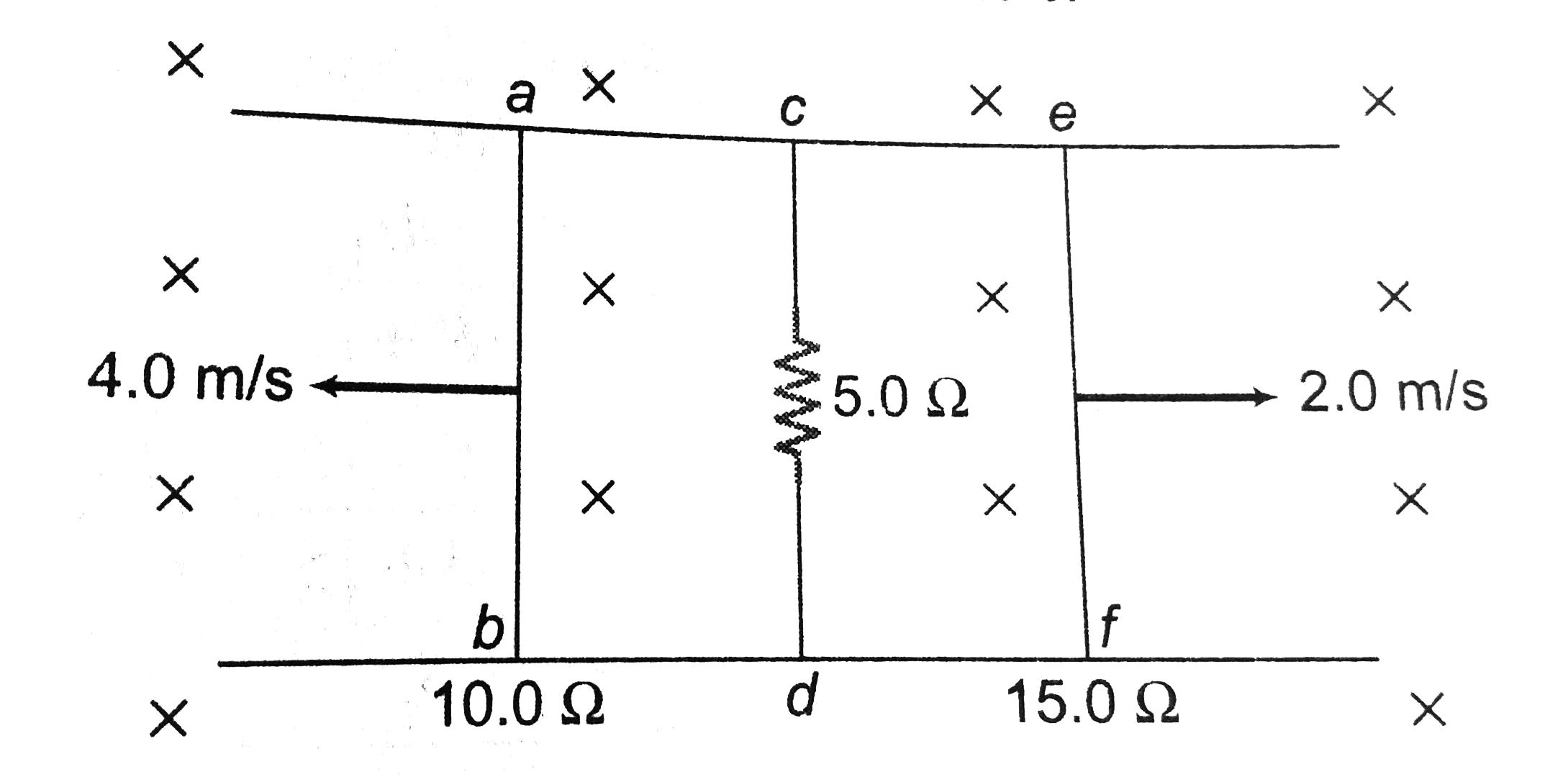
View SolutionTwo parallel rails with negligible resistance are 10.0 cm apart. The are connected by a 5.0Omega resistor. The circuit also contains two metal rods having resistances of 10.0Omega and 15.0Omega along the rails. The rods are pulled away from the resistor at constant speeds 4.00 m/\s and 2.00 m//s respectively. A uniform magnetic field of magnitude 0.01 T is applied perpendicular to the, plane of the rails. Determine the current in the 5.0Omega resistor.
View SolutionTwo parallel rails with negligible resistance are 10.0cm apart. They are connected by a 5.0 Omega resistor. The circuit also contains two metal rods having resistances of 10.0 Omega and 15.0 Omega along the rails. The rods are pulled away from the resistor at constant speeds 4.00 m/s and 2.00 m/s respectively. A uniform magnetic field of magnitude 0.01 T is applied perpendicular to the plane of the rails. Determine the current in the 5.0 Omega resistor.
View SolutionTwo vertical conducting rails separted by distance 1.0m are placed parallel to z -axis as shown in figure. At z=0 , a capacitor of 0.15 F is connected between the rails and a metal rod of mass 100g placed across the rails slides down along the rails. if a constant magnetic fields of 2.0 T exists perpendicular to the plane of the rails, what is the acceleration of the rod?
View SolutionA pair of long conducting rails are held vertical at a separation l = 50 cm . The top ends are connected by a resistance of R = 0.5 Omega and a fuse (F) of negligible resistance. A conducting rod is free to slide along the rails under gravity. The whole system is in a uniform horizontal magnetic field B = 1.5 T as shown. Resistance of the rod and rails are negligible and the rod remains horizontal as it moves. The rod is released from rest. Find the minimum mass of the rod that will ensure that the fuse blows out. It is known that rating of the fuse is 4 A.
View SolutionA rod with resistance R lies across frictionless conducting rails in a constant uniform magnetic field , as shown in the following figure. Assume the rails have negligible resistance. The magnitude of the force that must be applied by a person to pull the rod to the right at constant speed v is
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle theta to the horizontal. At the bottom, the rails are joined by a resistance R . There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle theta to the horizontal. At the bottom, the rails are joined by a resistance R . There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
View SolutionA conducting rod of length is moved at constant velocity v_(0) on two parallel, conducting, smooth, fixed rails, that are placed in a uniform constant magnetic field B perpendicular to the plane for the rails as shown in Fig. A resistance R is connected between the two ends of the rails. Then which of the following is/are correct:
View SolutionA conducting rod of length is moved at constant velocity on two parallel, conducting, smooth, fixed rails, that are placed in a uniform constant magnetic field B perpendicular to the plane for the rails as shown in Fig. A resistance R is connected between the two ends of the rails.
Then which of the following is/are correct:

View SolutionA conducting rod of length is moved at constant velocity on two parallel, conducting, smooth, fixed rails, that are placed in a uniform constant magnetic field B perpendicular to the plane for the rails as shown in Fig. A resistance R is connected between the two ends of the rails.
Then which of the following is/are correct:

View Solution