A copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
The correct Answer is:
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICSChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Comphension Based
Explore 3 Videos
- KINETIC THEORYBook:CENGAGE PHYSICSChapter:KINETIC THEORYExercise:Question Bank
Explore 31 Videos
- Magnetism and MatterBook:CENGAGE PHYSICSChapter:Magnetism and MatterExercise:Question Bank
Explore 50 Videos
Similar Questions
A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
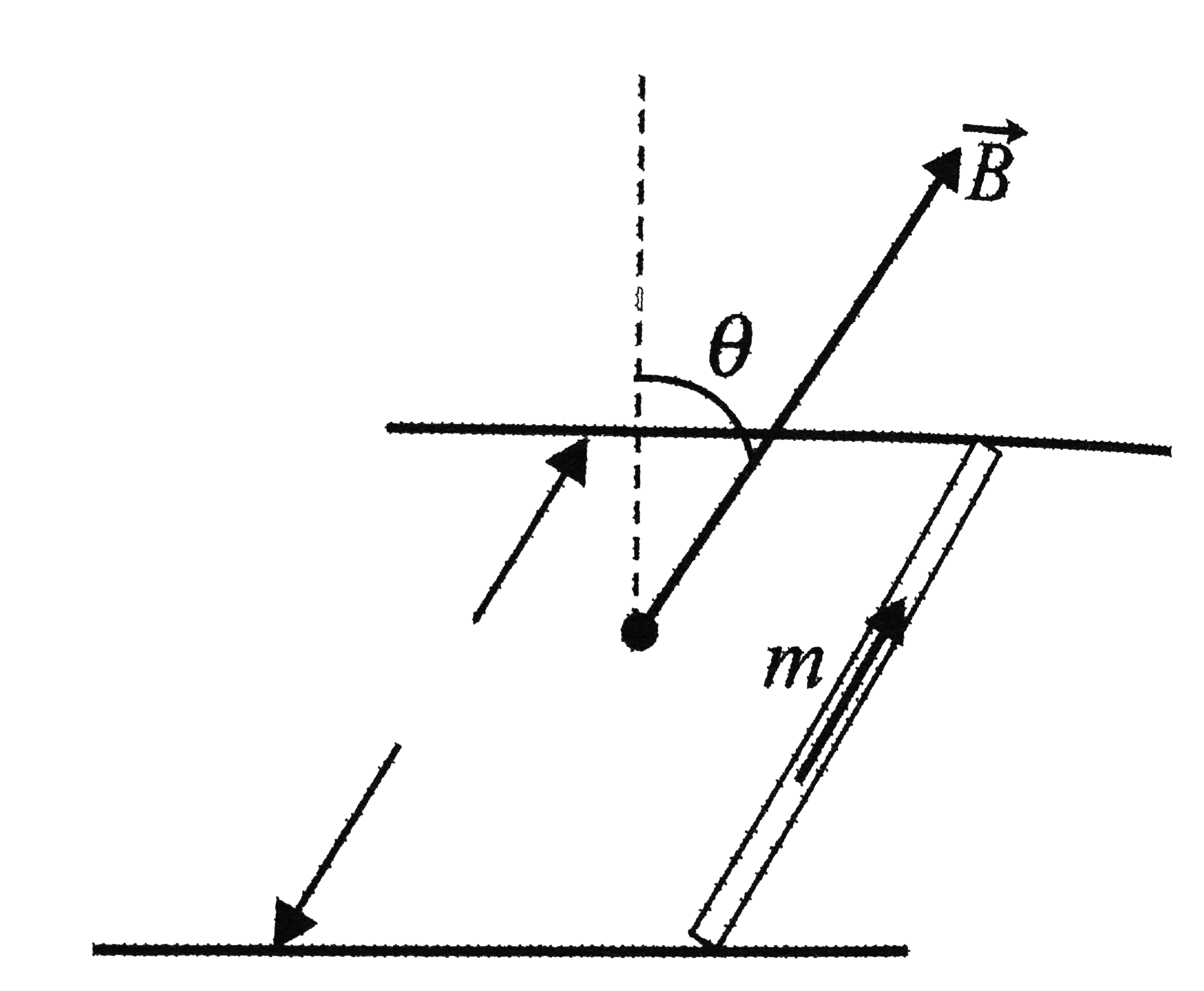
View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
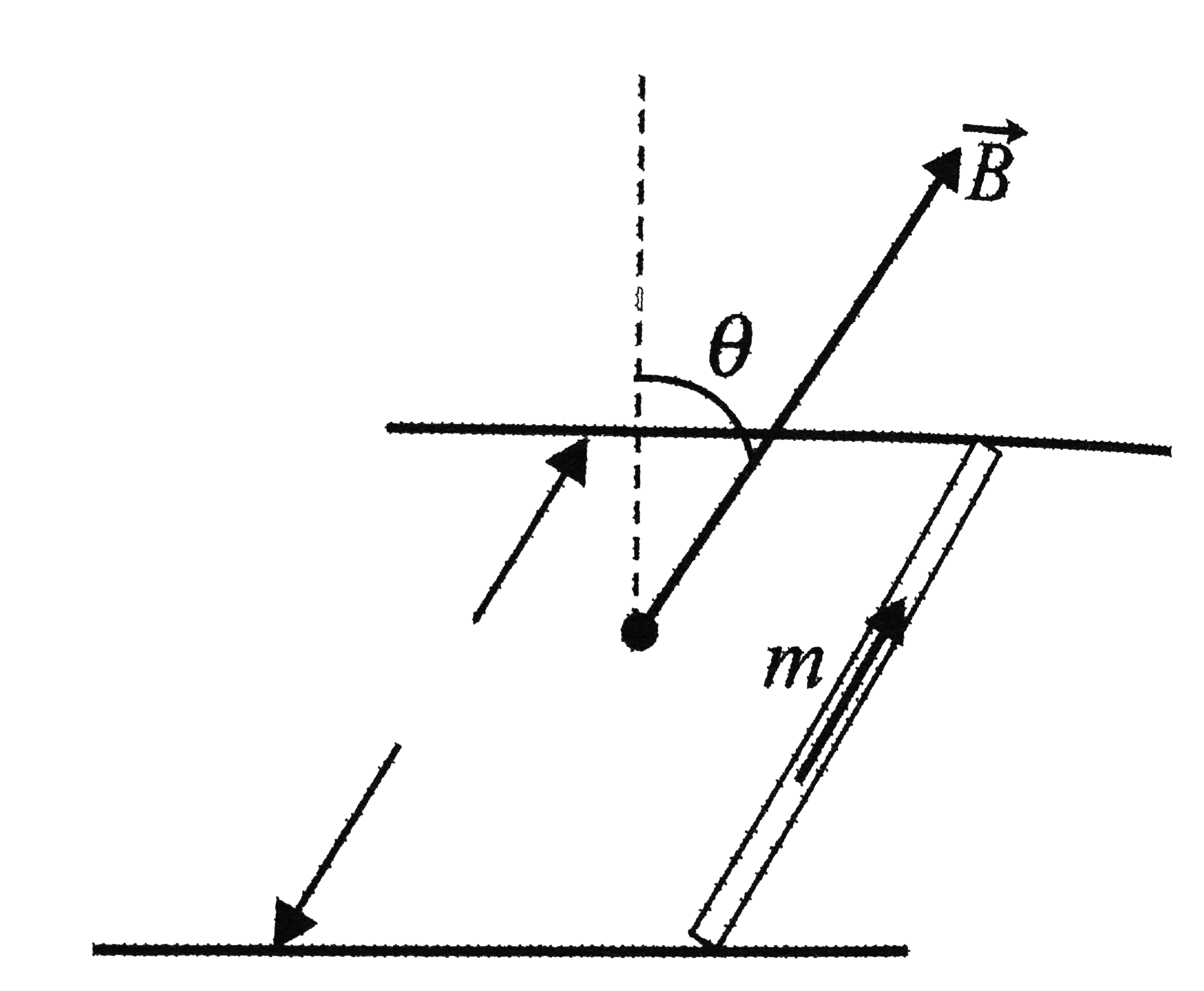
View Solution
Knowledge Check
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.
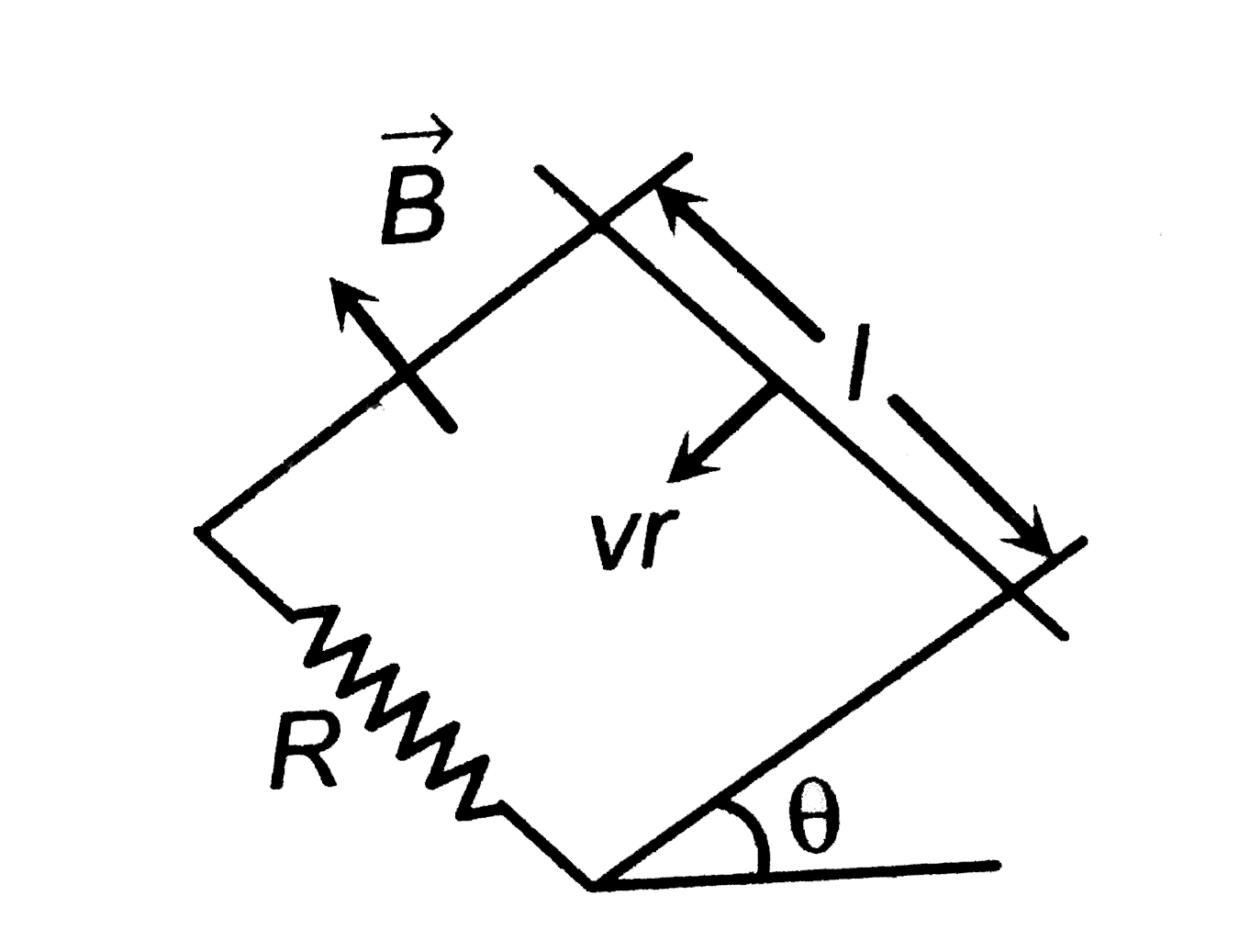
There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRtanθB2l2BmgRcotθB2l2CmgRsinθB2l2DmgRcosθB2l2A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRcosθB2l2BmgRsinθB2l2CmgRtanθB2l2DmgRcotθB2l2A rod of mass m and radius R rest on two parallel rails that are distance l apart and have a length L. The rod carries a current I( in the direction shown ) and rolls along the rails without slipping. A uniform magnetic field B is directed perpendicular to the rod and the rails. If it starts from rest, wat is the speed of the rod as it leaves the rails ?
 A√4BIlL3mB√3BIlL3mC√4BIlL2mD√BIlLm
A√4BIlL3mB√3BIlL3mC√4BIlL2mD√BIlLm
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
View SolutionA copper bar of mass m sides under gravity on two smooth parallel rails l distance apart and set at angle α to the horizontal . At the lop , the rails are joined by a resistor R. Calculate the steady velocity of the bar the n when there is a unifrom magnetic field B perpedicular to the plane of the rails .
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionOn an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
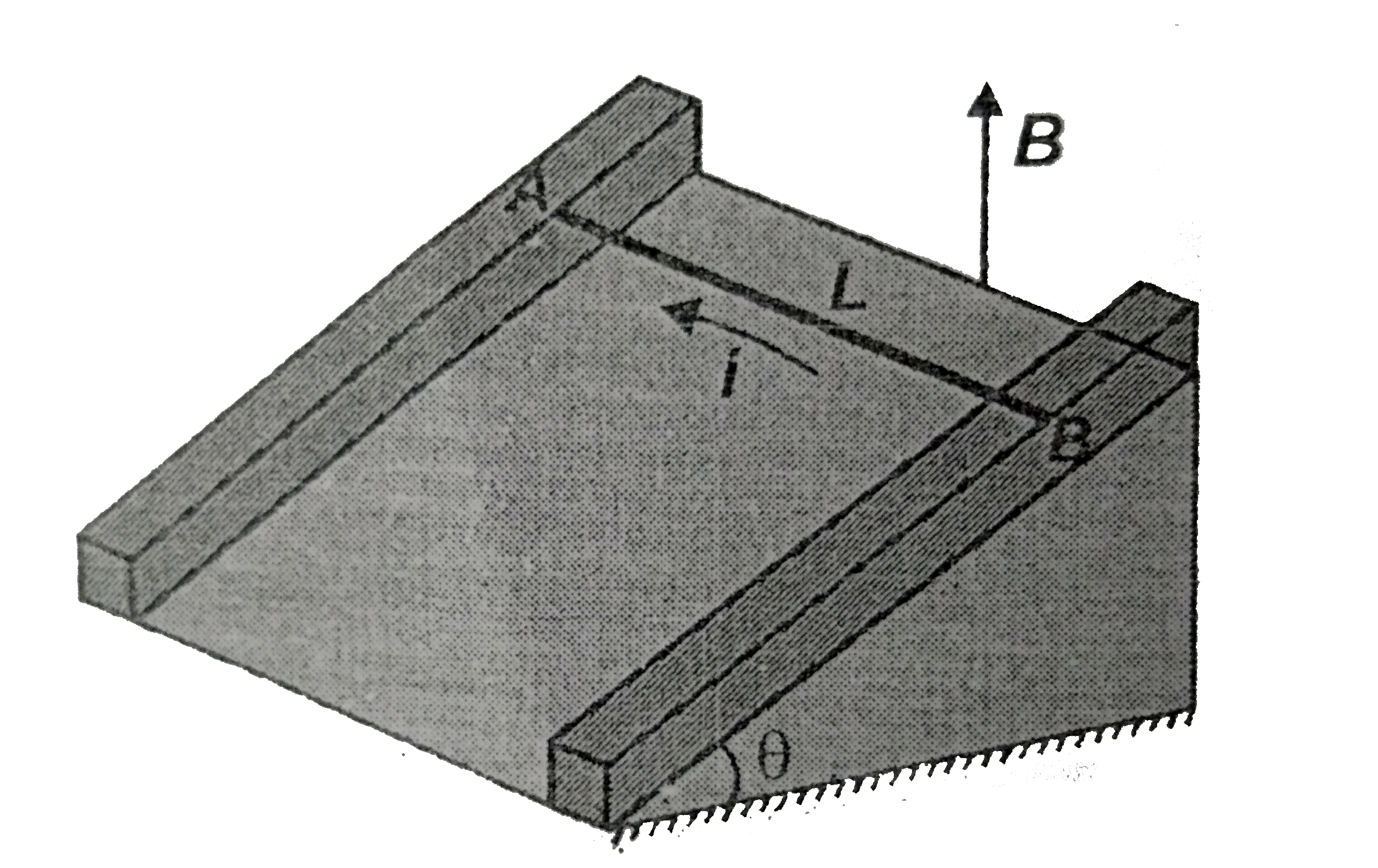
View Solution

