LINES AND ANGLES for Class 9 MATHS
INTRODUCTION
Hey guys, jaisa ki aap jante hai if we want to draw a line we need at least two points. Hum angles ke bare bhi previous classes me padh chuke hai sath hi hum parallel lines ke bare bhi padh chuke hai. In this chapter we will study the properties of the angles formed when two lines intersect each other, and also the properties of the angles formed when a line intersects two or more parallel lines at distinct points. Intersecting line ko transversal bhi kehte hai.
Basic Terms and Definitions
Sabse pehle friends hum kuch basic but very important terms dekhte hai. Ye sare terms and unke definitions is chapter ko smjhne ke liye bahut important hai , jinhe aache se samjh kr hum kuch important theorems dekhne wale hai and unse related questions practice karne wale hai.
Line Segment
A line which has two end points is called a line-segment. Line segment AB is denoted by ¯¯¯¯¯¯AB, and its length is denoted by AB.
Ray
A part of a line with one end point is called a ray. The ray AB is denoted by −−→AB.
Collinear Points
If three or more points lie on the same line, they are called collinear points, otherwise they are called non-collinear points.
Angle
An angle formed when two rays originate from the same end point. The rays making an angle are called the arms of the angle and the end point is called the vertex of the angle.
Acute angle
An angle measures between 0∘ and 90∘ is called acute angle. 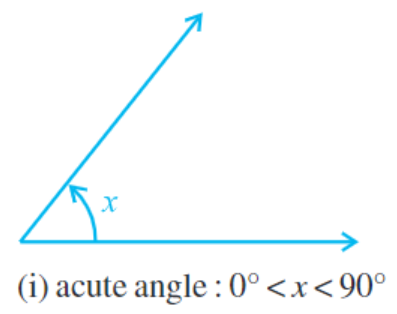
Right angle
An angle which is exactly equal to 90∘ is called right angle.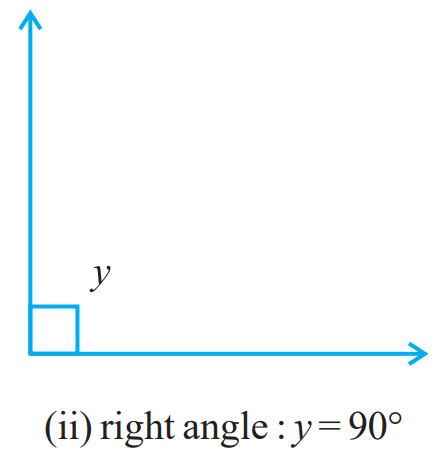
Obtuse angle
An angle greater than 90∘ but less than 180∘ is called an obtuse angle.
Straight line angle
An angle equal to 180∘ is called straight line angle.
Reflex angle
An angle which is greater than 180∘ but less than 360∘ is called a reflex angle.
Complementary angle
Two angles whose sum is 90∘ are called complementary angles. For example: 30∘+60∘ .
Supplementary angle
Two angles whose sum is 180∘ are called supplementary angles. For example 120∘+60∘ .
Adjacent angle
Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm means if we have two angles which touches each other on single ray but on different sides. 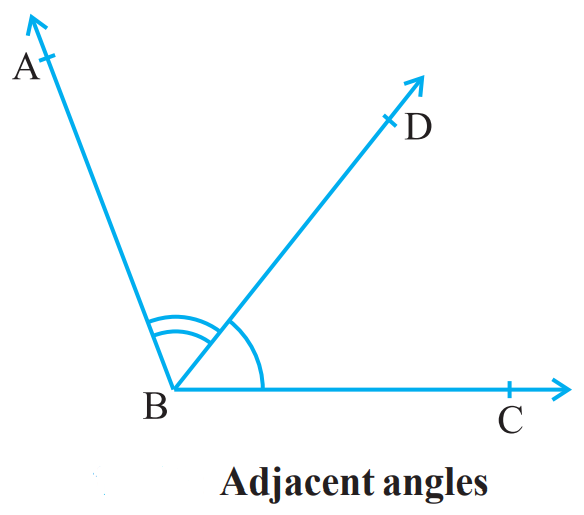
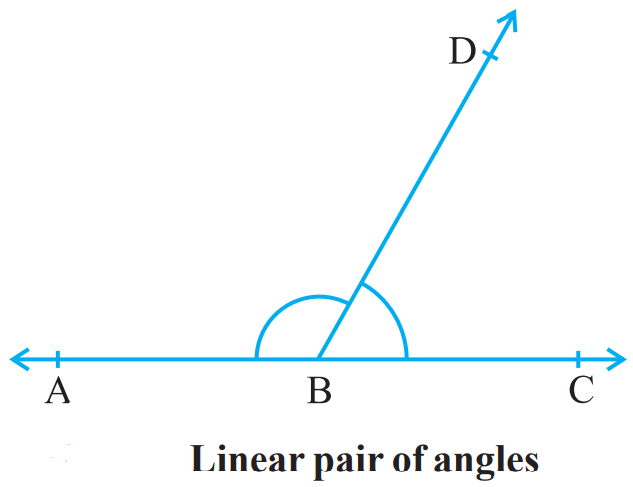
Linear pair
If sum of adjacent angles is 180∘ then they are called as linear pair .
Vertically opposite angle
When two line intersect each other then angle form opposite to each other are called vertically opposite angles.

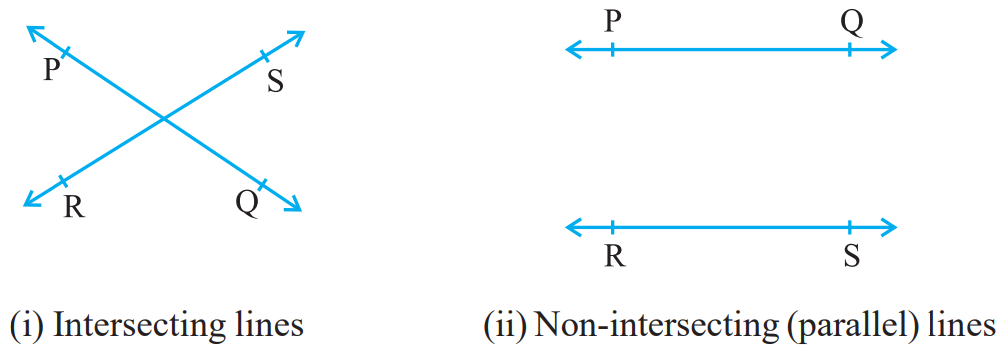
Intersecting Lines and Non-intersecting Lines
Man lo we have two lines PQ and RS. Now we extend them on both sides, if the lengths of the common perpendiculars at different points on these lines is different then both lines will intersect each other, jise intersecting lines kehte hai. If the lengths of the common perpendiculars at different points on these lines is the same then both lines will never intersect each other and are called parallel lines. Iska matlab hai ki, the distance between two parallel lines will be the same at every point .
Axiom 6.1
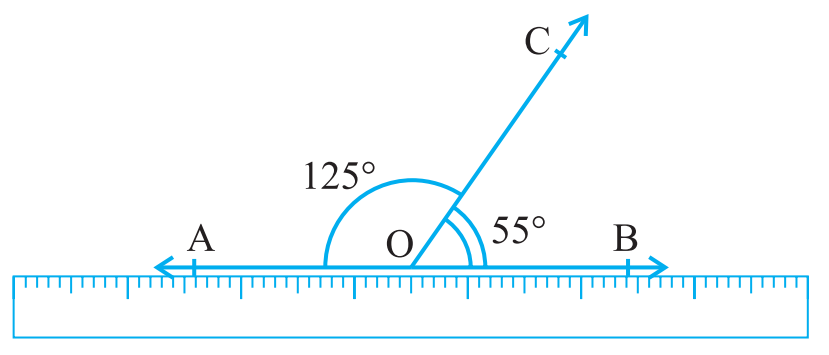
If a ray stands on a line, then the sum of two adjacent angles so formed is 180∘.

Here ∠AOC and ∠BOC are adjacent angle, therefore ∠AOC+∠BOC=∠AOB
If ∠AOC and ∠BOC is a linear pair of angles then ∠AOB=180∘
therefore we can write ∠AOC+∠BOC=180∘
Axiom 6.2
If the sum of two adjacent angles is 180∘, then the non-common arms of the angles form a line.
This two axioms together is called the Linear Pair Axiom.
Example 1
x and y froms a linear pair and y=3x−12∘. Find the values of x and y.
Since x and y froms a linear pair .
∴x+y=180∘
⇒x+3x−12∘=180∘ ( since y=3x−12∘)
∴4x=180∘+12∘
⇒4x=192∘
thus x=48∘
because x+y=180∘
So 48∘+y=180∘
now, y=180∘−48∘=132∘
∴x=48∘andy=132∘
Example 2
Find the values of a and b from the adjoining figure.
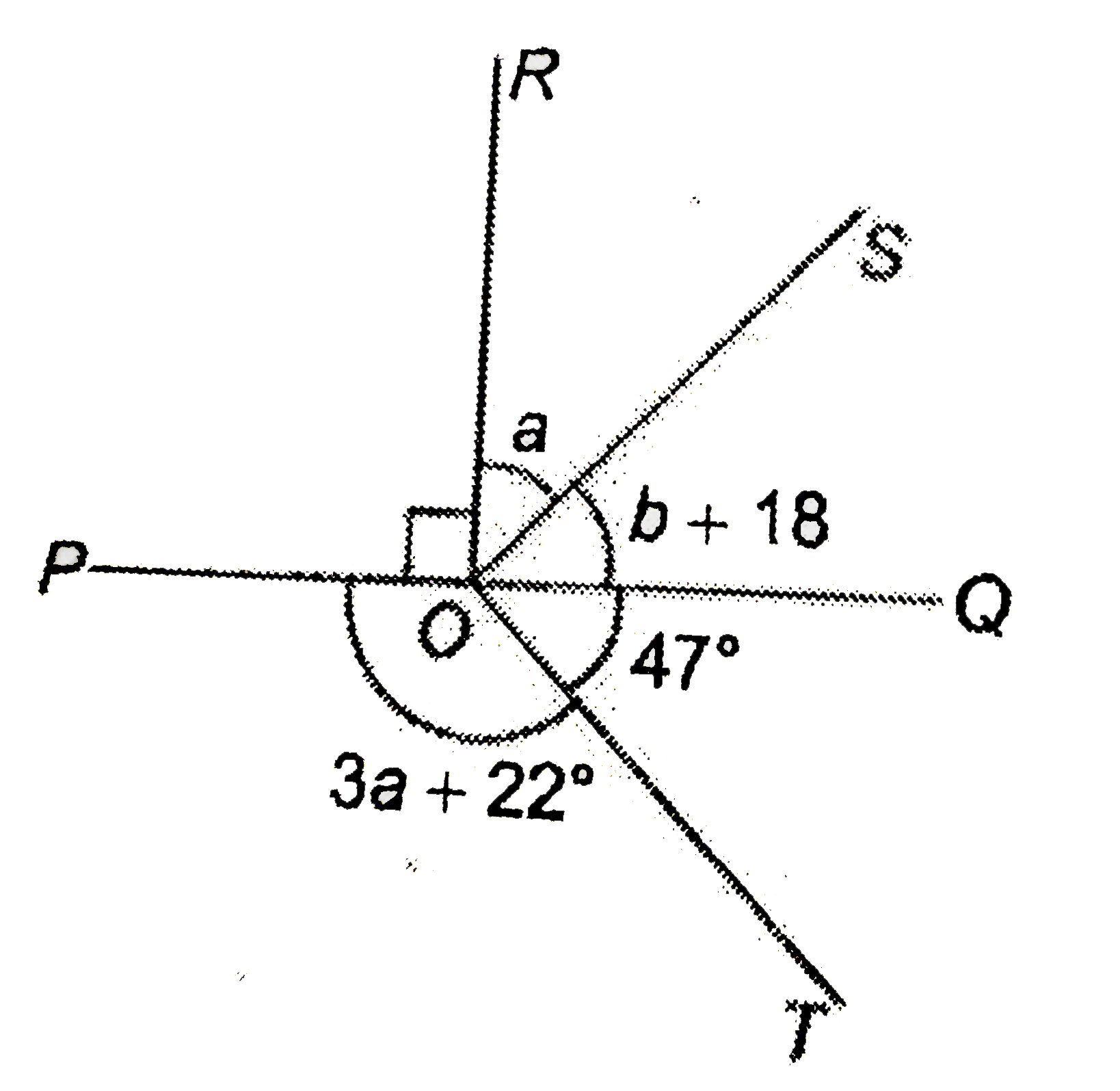
Since, OT stands on the straight line PQ,
So, ∠POT+∠QOT=180∘
⇒3a+22∘+47∘=180∘[Linear pair angles]
So, 3a=180∘−22∘−47∘=111∘
∴a=37∘ .....(1)
Also,
∠POR+∠ROS+∠SOQ=180∘ [angles on straight line]
So, 90∘+a+(b+18∘)=180∘
⇒90∘+37∘+b+18∘=180∘ [ from (1)]
∴b=180∘−145∘=35∘
Hence, a=37∘andb=35∘
Theorem 6.1
If two lines intersect each other, then the vertically opposite angles are equal.
Let AB and CD be two lines intersecting at O.
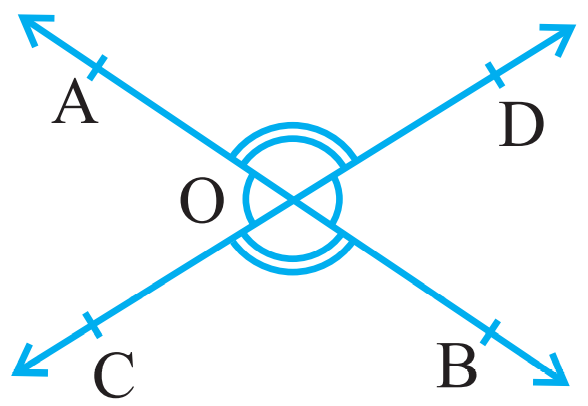
(i) ∠AOC and ∠BOD
(ii) ∠AOD and ∠BOC
will form two pairs of vertically opposite angles.
We need to prove that ∠AOC=∠BOD and ∠AOD=∠BOC.
Now, ray OA stands on line CD.
Therefore, ∠AOC+∠AOD=180∘ ................(1) [Straight line angles]
and ray OD stands on line AB.
Therefore, ∠AOD+∠BOD=180∘ ................(2) [straight line angles]
from (1) and (2)
∠AOC+∠AOD=∠AOD+∠BOD
This implies that ∠AOC=∠BOD .................(3)
Now CD is a straight line so
∠COA+∠AOD=180∘ ..............(4)
similarly ∠COB+∠BOD=180∘ .............(5)
From (4) and (5)
∠COA+∠AOD=∠COB+∠BOD
From (3) we have ∠AOC=∠BOD
∠AOD=∠COB .................(6)
(3) and (6) prove vertically opposite angles are equal.
Example 3
Ex 3. Find the values of a and b from the given figure when a−b=4∘

∠COE=∠DOF=90∘ (vertically opposite angle )
∠AOE+∠COE+∠BOC=180∘ (angles on same side of straight line)
⇒a+22∘+90∘+b+36∘=180∘
⇒a+b+148∘=180∘
⇒a+b=32∘ .....(1)
Given, a−b=4∘ .....(2)
Adding eqs. (1) and (2) we get, 2a=36∘
∴a=18∘
From eq. (1), 18∘+b=32∘
∴b=32∘−18∘=14∘
Hence, a=18∘,b=14∘
Parallel Lines and a Transversal
A line which intersects two or more lines at distinct points is called a transversal.
Figure ki help se hum ye dekh sakte hai ki line l intersects lines m and n at points P and Q respectively. Therefore, line l is a transversal for lines m and n.
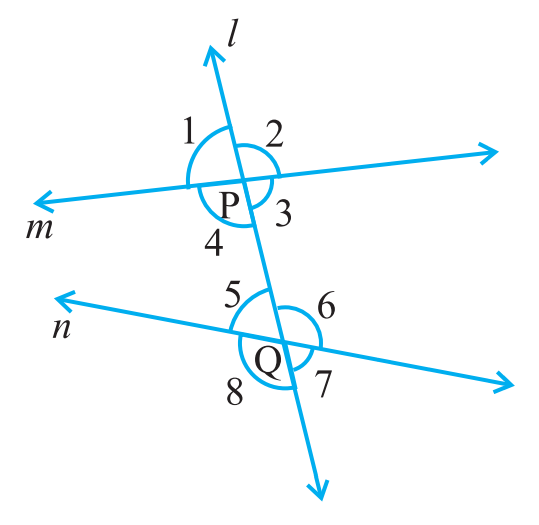
Yha humne sare angles ki marking kuch is prakar kar li hai i.e. ∠1,∠2,∠3,∠4,∠5,∠6,∠7and∠8
Yha hum sare angles ko two different group me divide kar sakte hai i.e.
Exterior angles :
∠1,∠2,∠7and∠8
Interior angles :
∠3,∠4,∠5and∠6
Here, we have some special pairs of angles which are as follows.
(a) Corresponding angles :
(i) ∠1and∠5
(ii) ∠2and∠6
(iii) ∠4and∠8
(iv) ∠3and∠7
(b) Alternate interior angles :
(i) ∠4and∠6
(ii) ∠3and∠5
(c) Alternate exterior angles :
(i) ∠1and∠7
(ii) ∠2and∠8
(d) Interior angles on the same side of the transversal :
(i) ∠4and∠5
(ii) ∠3and∠6
Interior angles on the same side of the transversal are also referred to as consecutive interior angles or allied angles or co-interior angles.
Axiom 6.3 : If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
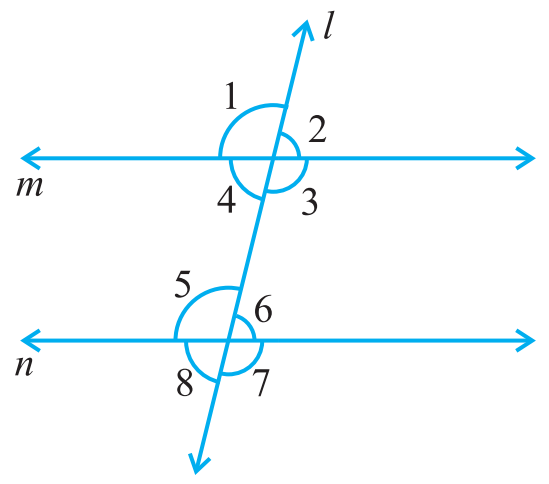
If m is parallel to n then ∠1=∠5,∠2=∠6,∠4=∠8 and ∠3=∠7
This referred as corresponding angle's axiom.
Axiom 6.4 : If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
This means if ∠1=∠5 or ∠2=∠6 or ∠4=∠8 or ∠3=∠7 then m is parallel to n.
Theorem 6.2
If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
Let transversal PS intersects parallel lines AB and CD at points Q and R 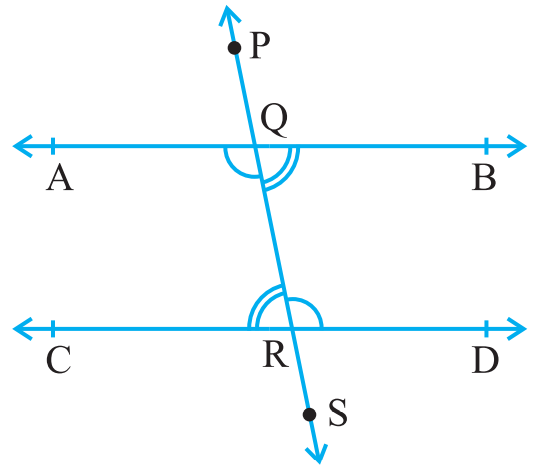
∠PQA=∠QRC ...............(1) [Corresponding angles axiom]
∠PQA=∠BQR ................(2) [vertical opposite angle]
from (1) and (2),
∠BQR=∠QRC(jo ki alterante interior angles hai)
similarly ∠PQB=∠QRD ..............(3) [Corresponding angles axiom]
∠PQB=∠AQR ................(4) [vertical opposite angle]
from (3) and (4),
∠AQR=∠QRD(jo ki alterante interior angles hai)
Theorem 6.3
If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
Let the transversal PS intersects lines AB and CD at points Q and R respectively such that ∠BQR=∠QRC.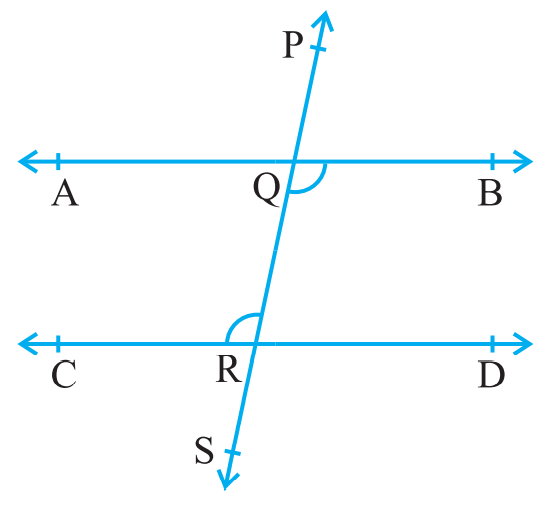
∠BQR=∠PQA ..............(1) [vertical opposite angles]
∠BQR=∠QRC ...............(2) [given]
from (1) and (2)
∠PQA=∠QRC
They are corresponding angles so from converse of corresponding angles axiom, hum ye keh sakte hai.
AB∣∣CD
Theorem 6.4
If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Let transversal PS intersects parallel lines AB and CD at points Q and R

Jaisa ki theorem 6.2 me humne dekha hai
∠BQR=∠QRC and ∠AQR=∠QRD ...............(1)
Now AQB form a straight line so ∠AQB=180∘
Similarly
∠AQR+∠RQB=180∘
since ∠AQR=∠QRD
So, ∠QRD+∠RQB=180∘.............(2)
and ∠AQR+∠QRC=180∘ [from (1) and (2)]
Therefore we can conclude that if a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Theorem 6.5
If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Let transversal PS intersects lines AB and CD at points Q and R such that ∠QRD+∠RQB=180∘ and ∠AQR+∠QRC=180∘

∠AQR+∠QRC=180∘ ...........(1) (given)
CD form a straight line so ∠CRD=180∘
Similarly
∠CRQ+∠QRD=180∘ .............(2)
from (1) and (2)
∠AQR+∠QRC=∠CRQ+∠QRD
∴∠AQR=∠QRD
Which are pair of alternate interior angles.
From theorem 6.3 hum ye keh sakte hai, if alternate interior angles is equal then the two lines are parallel.
Therefore, AB∣∣CD
Theorem 6.6
Lines which are parallel to the same line are parallel to each other.
Let a line t transversal for the lines l, m and n. It is given that line m ∣∣ line l and line n ∣∣ line l
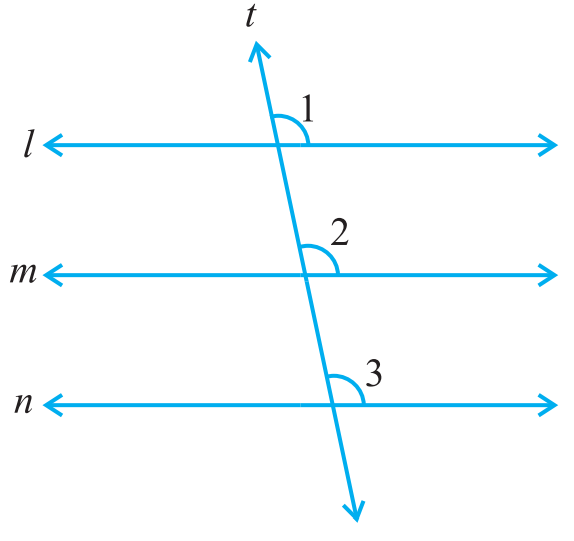
Since line m ∣∣ line l so,
∠1=∠2 ...........(1) [Corresponding angles axiom]
also line n ∣∣ line l so,
∠1=∠3 ............(2) [Corresponding angles axiom]
from (1) and (2) we get,
∠2=∠3
Therefore, Line m ∣∣ Line n [Converse of corresponding angles axiom]
Angle Sum Property of a Triangle
So guys, jaisa ki hum jante hai, sum of all the angles of a triangle is 180∘ to chalo kuch theorems and axioms ki help se ise prove bhi krke dekhenge.
Theorem 6.7
The sum of the angles of a triangle is 180∘.
Let PQR be triangle and ∠1,∠2 and ∠3, △PQR ke internal angles hain.
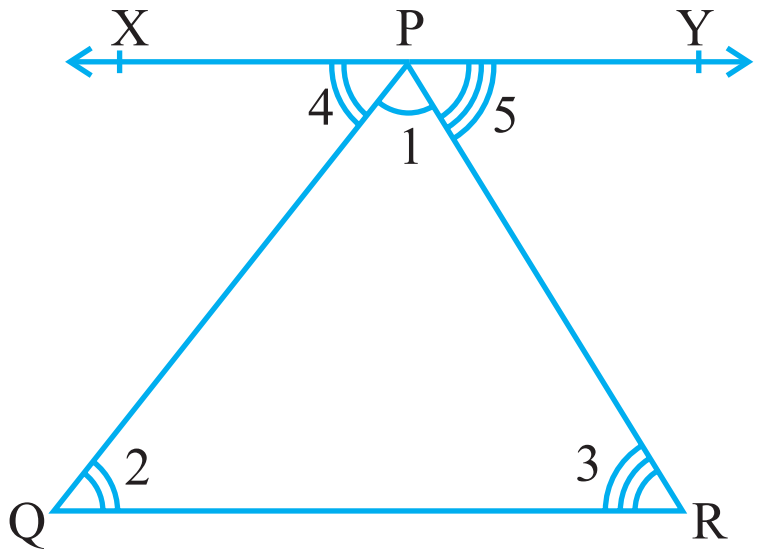
Construction : Draw a line XPY parallel to QR through the opposite vertex P
Now, XPY is a line,
Therefore, ∠4+∠1+∠5=180∘ .........(1)[Angles on a staright line]
But XPY∣∣QR, sath hi sath PQ and PR are two different transversals.
So, ∠4=∠2and∠5=∠3 [Pairs of alternate angles]
Substituting ∠4 and ∠5 in (1), we get
∠2+∠1+∠3=180∘
Or, ∠1+∠2+∠3=180∘
So hum ye conclude kar sakte hai, the sum of the angles of a triangle is 180∘.
Theorem 6.8
If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
Let PQR be triangle and ∠1,∠2 and ∠3 are the angles of △PQR.
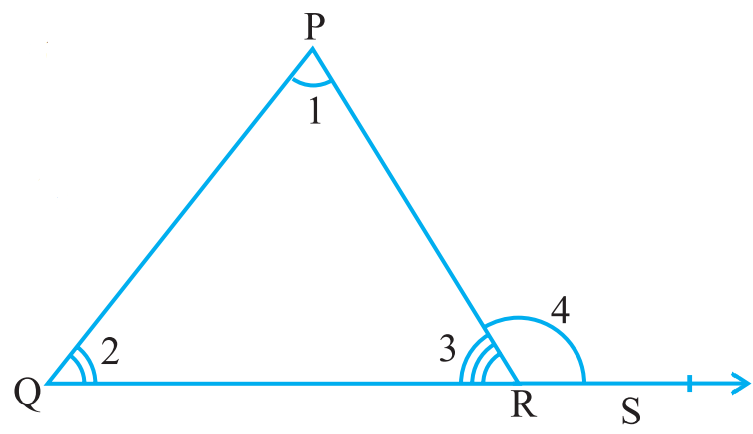
Side QR is produced to point S
Yha hum dekh sakte hai ki QRS is line so,
∠3+∠4=180∘ ...........(1) [Linear Pair]
Also, from theorem 6.7
∠1+∠2+∠3=180∘ ...(2)
From (1) and (2)
∠3+∠4=∠1+∠2+∠3
∴∠4=∠1+∠2
Therefore exterior angle ∠4 is equal to sum of interior opposite angles ∠1+∠2.
Example 4
In the given figure, AB∣∣CD. Find the values of x, y and z.

As we can see from the figure
75∘=y∘ [Alternate interior angles]
⇒y=75.
Now, ∠EGF+∠EGD=180∘ [Straight line]
⇒∠EGF+125∘=180∘⇒∠EGF=55∘.
Now, z∘+y∘+55∘=180∘ [Sum of angles of a triangle]
⇒z∘+75∘+55∘=180∘⇒z=50.
Now, x∘+y∘=180∘ [Angles on straight line]
⇒x+75=180⇒x=105.
∴x=105,y=75 and z=50.
Example 5
In the following figure AB||CD. Find ∠PQR and reflex angle PQR.
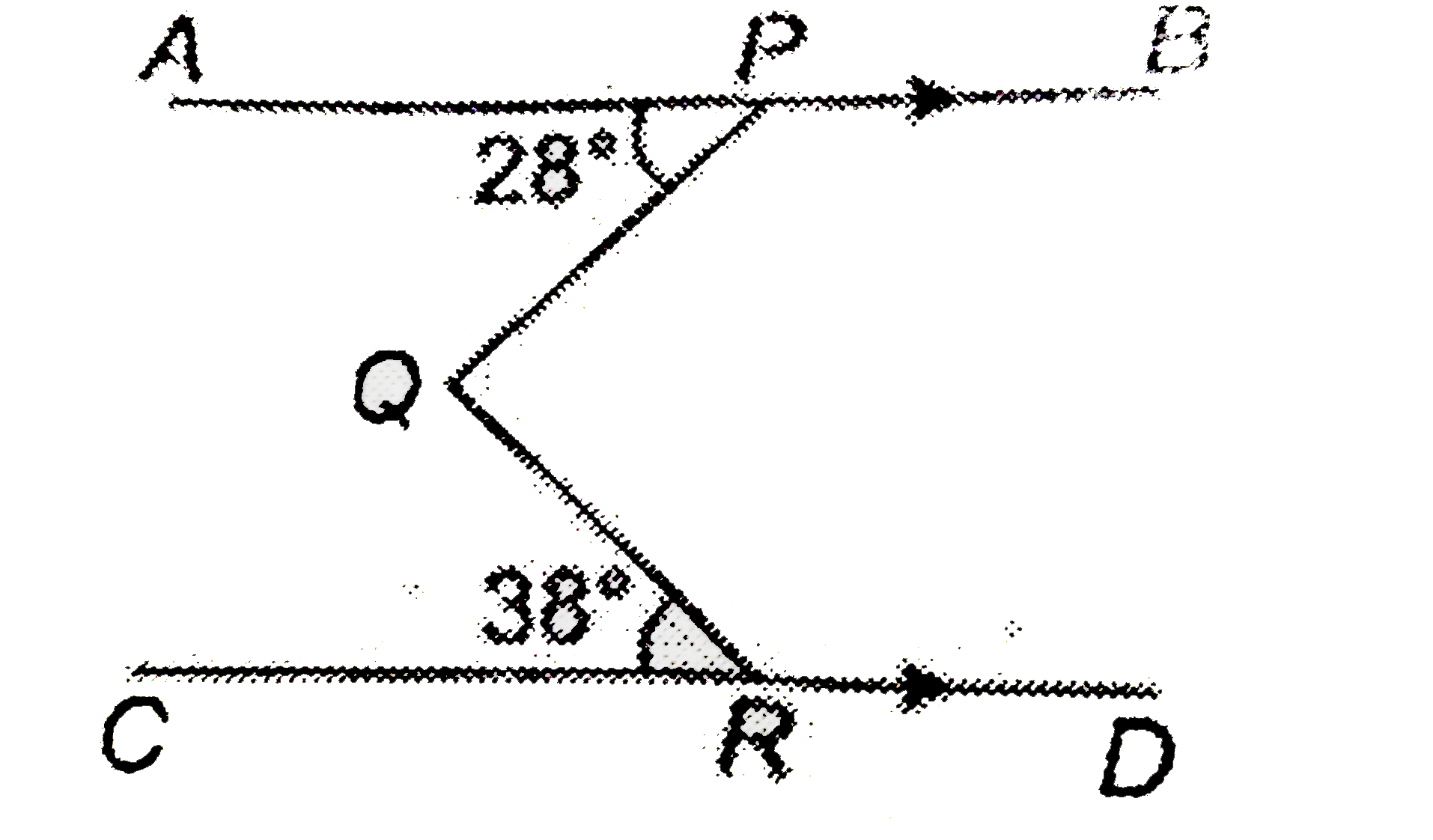
Draw a line EF through Q, parallel to AB.

As EF||AB and AB||CD, we get EF||CD
∠PQF=∠APQ=28∘ [alternate interior angles]
Again, ∠RQF=∠CRQ=38∘ [alternate interior angles]
∴∠PQR=∠PQF+∠RQF
=28∘+38∘=66∘
Reflex angle ∠PQR=360∘−∠PQR
360∘−66∘
∴ Reflex angle PQR =294∘
Example 6
In the given figure, AB||CD||EF. Find the value of x.

As we know from the given figure EF∣∣CD and EC is the transversal.
∴∠ECD+∠CEF=180∘ [Co interior angles]
⇒∠ECD+130∘=180∘⇒∠ECD=50∘.
Now, ∠ABC=∠BCD [alternative interior angles]
⇒70∘=x∘+50∘⇒x=20.
Example 7
In the given figure, AB∣∣CD. Find the value of x,y and z.

AB∣∣CD and BC is the transversal.
∴x∘=35∘ [alternate interior angles]
AB∣∣CD and AD is the transversal.
∴z∘=75∘ [alternate interior angles]
Now, x∘+y∘+75∘=180∘<br>⇒35∘+y∘+75∘=180∘⇒y∘=70∘
∴x=35,y=70andz=75.
Summary
Is chapter me humne following points ke bare detail me padha hai.
1. If a ray stands on a line, then the sum of the two adjacent angles so formed is 180° and vice-versa. This property is called as the Linear pair axiom.
2. If two lines intersect each other, then the vertically opposite angles are equal.
3. If a transversal intersects two parallel lines, then (i) each pair of corresponding angles is equal, (ii) each pair of alternate interior angles is equal, (iii) each pair of interior angles on the same side of the transversal is supplementary.
4. If a transversal intersects two lines such that, either (i) any one pair of corresponding angles is equal, or (ii) any one pair of alternate interior angles is equal, or (iii) any one pair of interior angles on the same side of the transversal is supplementary, then the lines are parallel.
5. Lines which are parallel to a given line are parallel to each other.
6. The sum of the three angles of a triangle is 180°.
7. If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.
Let's Revise
Line Segment : A line which has two end points is called a line-segment. Line segment AB is denoted by ¯¯¯¯¯¯AB , and its length is denoted by AB
Ray : A part of a line with one end point is called a ray. The ray AB is denoted by −−→AB. Is chapter me hum symbols ka use nahi karte huye simply ise AB se hi represent krenge.
Collinear Points : If three or more points lie on the same line, they are called collinear points, otherwise they are called non-collinear points.
Angle : An angle formed when two rays originate from the same end point. The rays making an angle are called the arms of the angle and the end point is called the vertex of the angle.
Acute angle : An angle measures between 0∘ and 90∘ is called acute angle.
Right angle : An angle which is exactly equal to 90∘ is called right angle.
Obtuse angle : An angle greater than 90∘ but less than 180∘ is called an obtuse angle.
Straight line angle : An angle equal to 180∘ is called straight line angle.
Reflex angle : An angle which is greater than 180∘ but less than 360∘ is called a reflex angle.
Complementary angle : Two angles whose sum is 90∘ are called complementary angles. For example: 30∘+60∘
Supplementary angle : Two angles whose sum is 180∘ are called supplementary angles. For example 120∘+60∘
Adjacent angle : Two angles are adjacent, if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm , means if we have two angles which touches each other on single ray but on different sides. 
Linear pair : If sum of adjacent angles is 180∘ i.e. supplementary angle so then adjacent angles are called linear pair of angles.

Note : All linear pairs are supplementary angles but all supplementary angles are not linear pair.
Vertically opposite angle : When two line intersect each other then angle form opposite to each other are called vertically opposite angles.

The distance between two parallel lines will be the same at every point.

Axiom 6.1 : If a ray stands on a line, then the sum of two adjacent angles so formed is 180∘.
Axiom 6.2 : If the sum of two adjacent angles is 180∘, then the non-common arms of the angles form a line. 
This two axioms together is called the Linear Pair Axiom.
Theorem 6.1 If two lines intersect each other, then the vertically opposite angles are equal.
Let AB and CD be two lines intersecting at O.

(i) ∠AOC = ∠BOD
(ii) ∠AOD = ∠BOC
A line which intersects two or more lines at distinct points is called a transversal.
Theorem 6.2 If a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.
Here ∠BQR=∠QRS and ∠AQR=∠DRQ
Theorem 6.3 If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
Theorem 6.4 If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Here ∠BQR+∠QRD=180∘
∠AQR+∠QRC=180∘
Theorem 6.5 If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Theorem 6.6 Lines which are parallel to the same line are parallel to each other.

If line l∣∣ line m and line m∣∣ line n then line l∣∣ line n.
Theorem 6.7 The sum of the angles of a triangle is 180∘.
Theorem 6.8 If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles. 
Here ∠4=∠1+∠2