CONTINUITY AND DIFFERENTIABILITY for Class 12 MATHS
Introduction
To bachcho, hum padhne vale hai about continuity and differentiability. Jaisa ki class 11th mein humne bhut sare functions ke differentiation ke bare mei padha hai; usi tarh se es class mein hum kuch naye functions ke differentiation ke baare mein padhenge jaise ki Inverse Trigonometric Function, Exponential Function, Logarithmic Function. Iske sath sath hum bahut sare complex functions ki continuity and differentiability ko bhi discuss karenge. Aur hum kuch interesting techniques sikhenge about differentiating Complex functions along with geometrical jo ki hume deep knowledge dega about continuity and differentiability.
Introduction
After studying about " Limits " , in our previous chapter , let us shift our domain to continuity. In this consider RHL and LHL in the graph. We need to start a graph either from " left " or from " right " such that there is no need to lift the pen . If there is a need to lift the pen than it is called as Discontinuous otherwise Continuous
Index
Continuity Definition|Cases for discontinous functions|Continuity in an interval and it's properties|Different functions in an interval|Removable type of discontinuity|Non-Removable type of discontinuity|The Intermediate value theorem|Differentiability| Right hand derivative and Left hand derivative|Geometrical representation of Differentiability
Let's Learn
Continuity agar hum simple language mein kahe to if a graph can be drawn without lifting a pen then it is known as continuous. continuity ki baat hmesha uski domain me hoti hai, then those points where the function is not defined ,should not be considered for the analysis .we always talk about continuity of graph ,unless mention naa ho agar usme break hoga kisi v point pe ya sharp corner hoga toh us point pe vo function differentiable nhi hoga, We learn from few examples.
Continuity Definition
A function f(x) is said to be Continuous if
limx→a−f(x)=limx→a+f(x) = F(a) i.e. LHL = RHL.
If a function is not Continuous than it is called as Discontinuous at x=a (see fig)
Example 1
y=sin|x|
to agar hum es graph ko dekhe to kya ye graph continuous hai ? Yes (kyonki hum bina pen uthaye graph draw kar saktey hai), lekin f(x)=0 is only point where we can see there is a sharp corner hai iska mtlb hai function continuous hai but function differentiable nhi hoga .from this example we can say agar koi function continuous hai iska mtlb ye nhi hai ki vo differentiable hoga . function may be not differentiable . Agar function diffrentiable hai toh ham surety ke sath bol skte hain vo continuous v hoga
To chalo ek aur example consider karte hai.
Cases for discontinous functions
So we have learnt a brief of continuity now these are the following cases of discontinuity.
( a ) limx→a−f(x)≠limx→a+f(x)
( b ) limx→a−f(x)=limx→a+(f(x) but not at x=a
( c ) f(a) is not defined
( d ) At least one of the limits does not exists.
Example 2
y=[x]
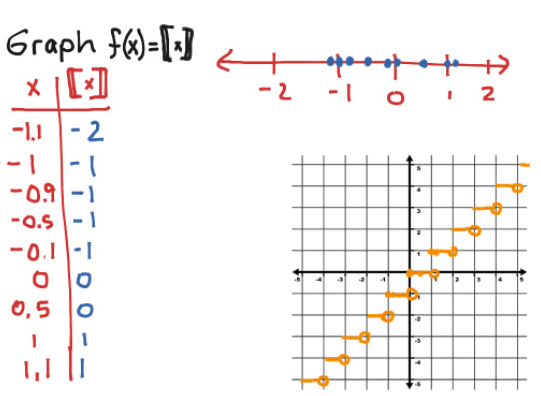
ye greatest integer function [x] ka graph hai jisme clearly dikh rha breaks hai har integer point pe.
we know that a greatest integer function by definition is if x lies between two successive integers then f(x) = least
f(x) is continuous at all the points except at integer points. So function discontinuous bhi hoga and non-differentiable bhi hoga.
Continuity in an interval and it's properties
In an interval (a,b) , a function is continuous only in this interval , only if
( i ) f is right continuous at a i.e. limx→a+f(x)=f(a)
( ii )f is left continuous at b i.e. limx→b−f(x)=f(b)
Let's discuss some properties based on these results
Let f(x) and g(x) be continuous , than
( a ) f(x)±g(x) is continuous at x=a
( b ) f(x)⋅g(x) is continuous
( c ) f(x)g(x) is also continuous , g(a)≠0
( d ) c⋅f(x) is continuous where c is constant
Note `to`
To in functions ko to humne graph se samjh liya lekin complex functions ke baare mei hum sirf graph se nhi bta sakte to uske liye ab hum theory padhenge. To sabse pehle hum function ki continuity ko uske fundamental theorey of continuity ki help se samjhte hai.
Example 1
Discuss the continuity of f(x)=|x|+|x−1| at x=0 and x=1.
f(x)=|x|={xx≥0−xx<0
and |x−1|={x−1x≥1−(x−1)x<1
∴f(x)=|x|+|x−1|=⎧⎪⎨⎪⎩1−2xx<010≤x<12x−1x≥1
At x=0 , f(0)=1
R.H.L=limx→0+=limh→0f(0+h)
=limh→01=1
L.H.L=limx→0−=limh→0f(0−h)
=limh→0{1−2(0−h)}=1
∴ R.H.L = f(0) = L.H.L
∴ f(x) is continuous at x=0 Hence proved.
In the same way we can prove for x=1 and the function is continuous at x=1 also
Continuity of a function
A function is said to be continuous at point x=a if LHL (Left Hand Limit) = RHL (Right Hand Limit)
f(a)=limx→a−f(x)=limx→a+f(x)
Chalo hum limits ko recall kartey hai.
Limit ka mtlb hota hai ki function ek value ko approach karega agar uss function ka input kisi value ko approach kar rha hai to.
Suppose f(x) ek function hai jo ek interval mein defined hai, and x=a is any point in that interval, then limit of f(x) is such that
limx→af(x)=f(a)
Kisi function ki limit ke exist karne ka meaning hai ki uss point per function ki left hand limit aur right hand limit ki value equal ho.
limit of y=f(x) at LHL ⇒ f(a)=limh→0f(a−h)
limit of y=f(x) at RHL ⇒ f(a)=limh→0f(a+h)
Mathematically hum isko aise likhte hai;
f(a)=LHL=RHL
f(a)=limh→0f(a−h)=limh→0f(a+h)
Note : Agar koi function kisi interval me defined hai aur iski definition continuous hai tab LHL aur RHL nikalne ke liye x ki value ko direct appropriate function mein rakh dete hai.
For example : Let f(x)={x2−1,x≤1−x2−1,x>1.<br><br>Findlimx→1f(x).
Soln.
We have
limx→1+f(x)=limh→0f(1+h)=limh→0{−(1+h)2−1}=limh→0(−2−h2−2h)=−2.
limx→1−f(x)=limh→0f(1−h)=limh→0{(1−h)2−1}=limh→0(1+h2−2h−1)
=limh→0(h2−2h)=0.
∴limx→1+f(x)≠limx→1−f(x).
Hence, limx→1f(x) does not exist.
at x=1 function is discontinuous point of discontinuity hai.
Example 2
If f(x)=sin(cosx)−cosx(π−2x)3,ifx≠π2andk,iff(x) is continuous at x=π2 , then k
Given that f(x) is continuous at x=π2
∴ k=limx→π/2=f(x)
∴k=limx→π/2=sin(cosx)−cosx(π−2x)3
⇒k=limx→π/2=sin(cosx)−cosxcos3x×sin3[(π/2)−x]8(π/2−x)3
⇒k=−16×18=−148 [∴limx→0sinx−xx3=−16]
Definition 1
Suppose f is a real function on a subset of the real numbers and let c be
a point in the domain of f. Then f is continuous at c if
limx→cf(x)=f(c)
a function is continuous at x=c if the function is defined at
x=c and if the value of the function at x=c equals the limit of the function at x=c. lf f is not continuous at c, we say f is discontinuous at c and c is called a point of discontinuity of f.
Example 3
If f(x)=⎧⎨⎩1−√2sinxπ−4x,x≠π4a ,x=π4
is continuous at x=π4 , It is given that f(x) is continuous at x=π4 , then a=? .
∴limx→π/4f(x)=f(π4)
⇒limx→π/41−√2sinxπ−4x=a
⇒√2limx→π/41√2−sinxπ−4x=a
⇒√24limx→π/4sinπ4−sinxπ4−x=a
⇒14√2limx→π/42sin(π8−x2)cos(π8+x2)(π8−x2)=a
⇒12√2cosπ4=a
a=(14)
Definition 2
A real function f is said to be continuous if it is continuous at every point
in the domain of f.
Suppose f is a function defined on a
closed interval [a,b], then for f to be continuous, it needs to be continuous at every point in [a,b] including the end points a and b. Continuity of f at a means
limx→a+f(x)=f(a)
and continuity of f at b means
limx→b−f(x)=f(b)
Observe that limx→a−f(x) and limx→b+f(x)
do not make sense. As a consequence
of this definition, if f is defined only at one point, it is continuous there, i.e., if the domain of f is a singleton, f is a continuous function.
Different functions in an interval
Some continous functions
Some discontinous functions
Algebra of continuous functions
Algebra of continuous functions ka matlab hai jab do functions ko add, subtract, multiply ya divide karte hai to jo nya function banta hai vo kaisa function banega continuous ya discontinuous aur discontinuous to kha kha discontinuous hoga.
Inh functions ko hum es tarh se define kar sakte hai, where c = continuous , f1 = function 1, f2 = function 2, d = discontinuous.
- cf1±cf2=cf (in the common domain)
- cf1×cf2=cf
- cf1cf2=cf (provided denominator is not equal to zero)
- cf1±dcf2=dcf
- cf1×dcf2=dcf
- dcf1±dcf2 = May or may not be continuous.
to chalo f(x)=sinxcosx ki continuity ko discuss karte hai. To dekho sinx(take it as f1) humara continuous function hai in it's domain aur cosx (take it as f2) bhi apne domain mein continuous hai toh algebra of continuous function se inka product bhi continuous hoga so, f(x)=sinxcosx is continuous for all xεR. (as cf1×cf2=cf)
Example 4
f(x)=⎧⎪⎨⎪⎩|x|+3ifx≤−3−2xif−3<x<36x+2ifx≥3
f(x)=⎧⎪⎨⎪⎩|x|+3ifx≤−3−2xif−3<x<36x+2ifx≥3
Here we will discuss the continuity of the function
At x=−3
So at f(−3)=|−3|+3=3+3=6
R.H.L. = limx→3+f(x)
=limh→0f(−3+h)
=limh→0f−2(−3+h)
=−2(−3+0)=6
L.H.L. = limx→3−f(x)
=limh→0f(−3−h)=limh→0|−3−h|+3
|−3−0|+3=3+3=6
⇒L.H.L.=f(−3)=R.H.L.
⇒f(x) is continuous at x=−3
At x=3
f(3)=6×3+2=20
L.H.L. = limx→3−f(x)
=limh→0f(3−h)
=limh→0−2(3−h)
−2(3−0)=−6
⇒f(3) ≠ L.H.L.
⇒f(x) is discontinuous at x=3
Theorem 1
STATEMENT : Suppose f and g be two real functions continuous at a real number c. Then
(1) f+g is continuous at x=c.
(2) f–g is continuous at x=c.
(3) f.g is continuous at x=c.
(4) fg is continuous at x=c, (provided g(c)≠0)
(1) We have
limx→c(f+g)(x)=limx→c[f(x)+g(x)] (by definition of f+g)
=limx→cf(x)+limx→cg(x) (by the theorem on limits)
=f(c)+g(c) (as f and g are continuous)
=(f+g)(c) (by definition of f+g)
(2) We have
limx→c(f−g)(x)=limx→c[f(x)−g(x)] (by definition of f−g)
=limx→cf(x)−limx→cg(x) (by the theorem on limits)
=f(c)−g(c) (as f and g are continuous)
=(f−g)(c) (by definition of f−g)
(3) We have
limx→c(fg)(x)=limx→c[f(x).g(x)] (by definition of fg)
=limx→cf(x).limx→cg(x) (by the theorem on limits)
=f(c).g(c) (as f and g are continuous)
=(fg)(c) (by definition of fg)
(4) We have
limx→c(fg)(x)=limx→c[f(x)g(x)] (by definition of fg)
=limx→cf(x)limx→cg(x) (by the theorem on limits)
=f(c)g(c) (as f and g are continuous)
=(fg)(c) (by definition of fg)
NOTE: if g is the constant function, g(x)=λ then the
function λf defined by λf(x)=λf(x) is continuous wherever g(x)≠0. In particular, the continuity of g implies continuity of 1g
Removable type of discontinuity
Sometimes limit f(x) is not equal to f(a) than the function is said to be Removable discontinuity of first kind. It can be classified further into two types.
(a)Missing point discontinuity:When limit of f(x) exists but f(a)is¬def∈ed<br><b>(b)Isolatedp∮discont∈uity:<b>When⊥hlimitoff(x)andf(a) exists but both are not equal.
Theorem 2
STATEMENT : Suppose f and g are real valued functions such that (fog) is defined at c. If g is continuous at c and if f is continuous at g(c), then (fog) is continuous at c.
Since fog is defined. Therefore,
Range (g) ⊂ Domain (f)
⇒g(x)∈ Domain (f) for all x∈ Domain (g)
Now,
g(x) is continuous at x=a
⇒limx→ag(x)=g(a)
and f is continuous at g(a)
⇒limg(x)→g(a)f(g(x))=f(g(a))
limx→a(fog)(x)=limx→a(f(g(x)))
=f(limx→ag(x))
⇒limx→af(g(x))=f(g(a))
⇒limx→a(fog)(x)=(fog)(a)
fog is continuous at x=a
Example 5
Discuss the continuity of the functions at the points shown against them . If a function is discontinuous , determine whether the discontinuity is removable . In this case , redefine the function , so that it becomes continuous : f(x)=xsin(1x) , for x≠0=0 , for x=0⎫⎬⎭ at x=0
f(0)=0 …(Given)…(1)
limx→0f(x)=limx→0xsin1x
Since −1≤sin1x≤1 asx≠0
∴−x≤xsin1x≤x
∴limx→0(−x)≤limx→0xsin1x≤limx→0(x)
∴0≤limx→0f(x)≤0
∴limx→0f(x)=0 ...(2)
From (1) and (2) , limx→0f(x)=f(0)
∴f is continuous at x=0.
Example 3
Show that the function f(x)={3x−2whenx≤0x+1whenx>0
is discontinuous at x=0
We have f(0)=(3×0−2)=−2
limx→0+f(x)=limh→0f(0+h)
limh→0(h+1)=1
limx→0−f(x)=limh→0f(0−h)
limh→0[3(−h)−2]=limh→0(−3h−2)=−2
limx→0+f(x)≠limx→0−f(x)and∴limx→0f(x) does not exist.
Hence, f(x) is discontinuous at x=0
Example 6
Discuss the continuity of the functions at the points shown against them . If a function is discontinuous , determine whether the discontinuity is removable . In this case , redefine the function , so that it becomes continuous :
F(x)=4x−ex6x−1 , for x≠0=log(23) , for x=0⎫⎪⎬⎪⎭ at x=0.
f(0)=log(23) ...(Given)...(1)
limx→0f(x)=limx→04x−ex6x−1
=limx→0(4x−1)−(ex−1)6x−1
=limx→0(4x−1x)−(ex−1x)(6x−1x) ... [ x→0 , x≠0 ]
=limx→04x−1x−limx→0ex−1xlimx→06x−1x
=(log4)−1log6 ...[∵limx→0ax−1x=loga]
∴limx→0f(x)=(log4)−1log6 ...(2)
From (1)and(2) , limx→0f(x)≠f(0)
∴f is discontinuous at x=0.
Here limx→0 f(x) exists but not equal to f(0). Hence, the discontinuity at x=0 is removable and can be removed by redefining the function as follows :
f(x)=4x−ex6x−1,forx≠0
=(log4)−1log6,forx=0.
Differentiability
Let f is a real function and c is a point in its domain. The derivative of f at c is defined by limh→0f(c+h)−f(c)h
provided this limit exists. Derivative of f at c is denoted by f′(c) or ddx(f(x))∣∣∣c. The function defined by f′(x)=limh→0f(x+h)−f(x)h
wherever the limit exists is defined to be the derivative of f. The derivative of f is denoted by f′(x) or ddx(f(x)) or if y=f(x) by dydx or y′. The process of finding derivative of a function is called differentiation.
The following rules were established as a part of algebra of derivatives.
(1) (u±v)′=u′±v′
(2) (uv)′=u′v+uv′ (Leibnitz or product rule)
(3) (uv)′=u′v−uv′v2, wherever v≠0 (Quotient rule)
Derivative of some standard function
ddx(xn)=nxn−1 n∈R(n must be real numbers)
ddx(sinx)=cosx
ddx(cosx)=−sinx
ddx(tanx)=sec2x
ddx(cosecx)=−cosecxcotx
ddx(secx)=secxtanx
ddx(cotx)=−cosec2x
ddx(cf(x))=cddx(f(x))
to ab hum differentiation ko thoda aur detail mein samjhte hai. Do you know Every differentiable function is continuous but the converse is not true. Jitne bhi continuous function hai agar vo differentiable hai kisi point ya kisi interval mein to vo continuous bhi hoga. Ab uska converse dekhte hai, converse karne ka matlab kya hai ki agar function continuous hoga to differentiable bhi hoga to yeh true nhi hai so, next theorem mei hum isko prove karenge.
Non-Removable type of discontinuity
Sometimes limx→af(x) does not exists and it is not possible to redefining . It can be further classified.
- Finite type of discontinuity: In such type the LHL and RHL exists but not equal .
- Infinite type of discontinuity: In this either LHL or RHL tends to infinity .
Differentiability
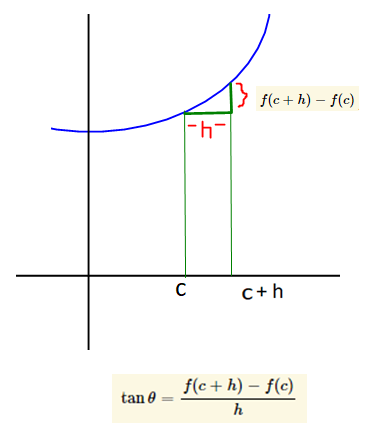
A function f is differentiable at c (where c is in domain) if limh→0f(c+h)−f(c)h and limh→0f(c−h)−f(c)−h both are finite and equal to f′(c) and function f is not differentiable at c if limh→0f(c+h)−f(c)h does not exist. A function is said to be differentiable in an interval [a,b] if it is differentiable at every point of [a,b].
Example 6
Does the following function not defined at x=0 has non-removable discontinuity at the point x=0?
f(x)=11+21x
f(a−)≠f(a+) means at x=0 limit is not defined
∴f(0+)=limh→0+⎛⎝11+21h⎞⎠→0
f(0−)=limh→0−⎛⎝11+21h⎞⎠→1
So it is a non removable discontinuity
Theorem 3
STATEMENT: If a function f is differentiable at a point c, then it is also continuous at that point.
Since f is differentiable at c, we have
limx→cf(x)−f(c)x−c=f′(c)
But for x≠c, we have
f(x)−f(c)=f(x)−f(c)x−c⋅(x−c)
Therefore limx→c[f(x)−f(c)]=limx→c[f(x)−f(c)x−c⋅(x−c)]
or limx→c[f(x)]−limx→c[f(c)]=limx→c[f(x)−f(c)x−c]⋅limx→c[(x−c)]
or =f′(c)⋅0=0
or limx→cf(x)=f(c)
Hence f is continuous at x=c.
Therefore, Every differentiable function is continuous.
The Intermediate value theorem
Let y=f(x) is a continuous function in between (a,b) such that y0 lies in between f(a) and f(b) and c lies in between (a,b)
Note: For the function to have atleast one solution in between the intervals , the "product" of f(a) and f(b) should be negative.
Derivatives of composite functions
Derivative of composite function ki agar hum baat karte hai to hmare pass ek notation ati hai
fog = function of function, that is also known as composition of function, or
= f is composed with g
iska basic matlab hai jo function y hai i.e. y=fg(x) ki form mei hai that means normally kya hota hai function y=f(x) ki form mein hota hai that is x is the function of y isi tarh se y=f(g(x)) mei, jo g(x) hai vo y ka function hai aur x jo hai g ka function hai, to ye ek tarh ka composition ban rha hai ki x→g→y ye ek meaning yha pe samjh ata hai to ab hum iska derivative nikalenge
fog→ Derivative of fog, dydx = (fog)'(x) = f'(g(x))×g'(x)
esse hum example se samjhte hai
Let f(x)=(x+1)2=x2+2x+1
ddxf(x)=2x+2
If we note that ddxf(x)=2(x+1) which is
ddxf(x)=dd(x+1)(x+1)2.ddx(x+1)
Since here power of (x+1) is small but if we have higher power such observation is that it simplifies the calculation in finding the derivative.
Example 7
Let f:[0,1] →[0,1] be a continuous function . Then prove that f(x)=x for at least one 0≤x≤1.
Let us take g(x)=f(x)−x
g(0)=f(0)–0=f(0)≥0 {0≤f(x)≤1}
g(1)=f(1)–1≤0
⇒g(0)⋅g(1)≤0
⇒g(x)=0 has atleast one root in [0,1]
⇒f(x)=x for atleast one x ∈[0,1]
"
Theorem 4
(Chain Rule) Let f be a real valued function which is a composite of two functions u and v i.e., f=vou. Suppose t=u(x) and if both dtdx and dvdt exist, we have
dfdx=dvdt⋅dtdx
and if f is a real valued function which is a composite of three functions u, v and w i.e.,
f=(wou)ov. If t=v(x) and s=u(t), then
dfdx=d(wou)dt⋅dtdx=dwds⋅dsdt⋅dtdx
provided all the derivatives in the statement exist.
to chalo example se samjhte hai let's say hume f(x)=(3x+1)5 ka derivative find out karna hai to dekho es example mei function hai 3x+1 upto 5th power. So, yha per do function hai (3x+1)(inside function) aur isko hume 5th power tak consider karna hai (outside function). Ab, aapko pta hai by power rule, derivative of x5 is 5x4. To ek minute ke liye hum 3x+1 ko x manenge so iska derivative kya hua 5(3x+1)4 lekin humne function ko x mana tha but ye x hai nhi to hume (3x+1) ke derivative ko function se multiply karna hai and then we have to simplify to get the final answer
f(x)=(3x+1)5
f'(x)=ddx(3x+1)5
=5(3x+1)4⋅ddx(3x+1)
=5(3x+1)4(3)
=15(3x+1)4.
Example 8
Use the Intermediate Value Theorem to show that the polynomial function f(x)=x3+2x−1 has a zero in the interval [0,1].
So let us find f(1) = 13 + 2⋅1 - 1 = 2
f(0) = 03 + 0 - 1 = −1
So here f(1) is positive and f(0) is negative .
∴ there will be a point were the value of f(x) = 0
Hence proved
Derivatives of implicit functions
Vo functions jo x aur y dono variable ki form mien hote hai but separated hote hai unhe explicit function of x khte hai, in the form of y=f(x). Aur agar hum function ko separate na kr paye to es tarah ke functions ko implicit function khte hai.
For example, cosy=sin(xy)+cosx
To find differentiation of such function we will differentiate whole expression both side. To calculate dydx
ddx(cosy)=ddx(sin(xy)+cosx)
ddx(cosy)=ddx(sin(xy))+ddx(cosx)
ddy(cosy).dydx=ddxy(sin(xy)).dxydx+ddx(cosx)
−sinydydx=cos(xy)(y+xdydx)+(−sinx)
dydx(xcos(xy)+siny)=sinx−ycos(xy)
dydx=sinx−ycos(xy)xcos(xy)+siny
Note:
( a ) If f(x) and g(x) are discontinuous at x=a but still f(x)±g(x) not necessarily be discontinuous .
( b )The domain of a closed interval must have the range in the same interval .
( c ) If f is continuous at x=a & g is continuous at x=f(a) then the composite g[f(x)] is continuous at x=a .
For example f(x)=xcosxx2+1 and g(x)=|x| are continuous at x=0
So g(f(x))=∣∣∣xcosxx2+1∣∣∣ is also continuous at x=0
Example 4
If cos(x+y)=ysinx, find dydx.
On differentiating both sides of (i) w.r.t. x, we get
−sin(x+y).ddx(x+y)=ycos+sinx.dydx
⇒−sin(x+y)(1+dydx)=ycosx+sinx.dydx
⇒{sin(x+y)+sinx}.dydx=−{sin(x+y)+ycosx}
⇒dydx=−{sin(x+y)+ycosx}{sin(x+y)+sinx}.
Example 9
If f(x)=x2+1x2−1andg(x)=tanx , then discuss the continuity of fog(x) .
g(x)=tanx , x≠nπ+(π2)
f(x)=x2+1x2−1 , x≠±1
f(og)=1+tan2xtan2x−1=sec2xtan2x−1
x≠nπ+(π2)
tanx≠±1
x≠nπ±(π4)
Derivatives of inverse trigonometric functions
Humme pta hai inverse trigonometric functions continuous functions hote hai, lekin hum eshe prove nhi karenge hum simply chain rule ka use karke inka derivative find karenge.
(1) ddx(sin−1x)=1√1−x2
Proof: Let y=sin−1x Then, x=siny
Differentiating both sides w.r.t. x, we get
1=cosydydx
which implies that dydx=1cosy=1cos(sin−1x)
or we can also eliminate cos and sin function
we know sin(sin−1x)=x then cos2y=1−(siny)2=1−(sin(sin−1x))2=1−x2
⇒cosy=√1−x2
dydx=1cosy=1√1−x2
Domain of f′=(−1,1)
Similarly we can prove other inverse trigonometric functions as
(2) ddx(cos−1x)=−1√1−x2
Domain of f′=(−1,1)
(3) ddx(tan−1x)=11+x2
Domain of f′=R
(4) ddx(cosec−1x)=−1x√x2−1
Domain of f′=(−∞,−1)∪(1,∞)
(5) ddx(sec−1x)=1x√x2−1
Domain of f′=(−∞,−1)∪(1,∞)
(6) ddx(cot−1x)=−11+x2
Domain of f′=R
Example 10
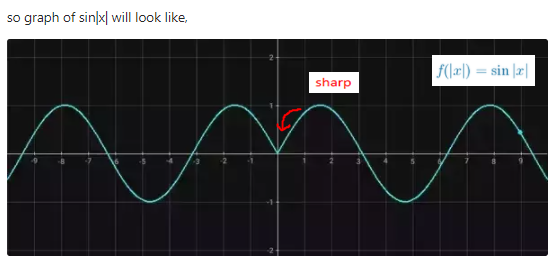
Examine that sin |x| is a continuous function.
Let g(x)=|x| and h(x)=sinx
We know that g(x)=|x| is continuous for x ∈ R .
and h(x)=cosx is also continuous for each x ∈ R .
Now (hog)(x) = h[g(x)] = h[|x|] = sin|x|
⇒g(x)andh(x) both are continuous functions .
∴ Composite function (hog)(x) is also a continuous function .
⇒sin|x| is continuous for all x ∈ R .
Example 5
Differentiate w.r.t. x :
cot−1(1x)
Let y=cot−1(1x).
Putting x=tanθ, we get
y=cot−1(1tanθ)=cot−1(cotθ)=θ=tan−1x.
∴dydx=1(1+x2).
Hence, ddx{cot−1(1x)}=1(1+x2).
Differentiability
Let y=f(x) is function continuous at (a,b) . Than differentiability of f(x) w.r.t x denoted by
dydx = limΔx→0f(x+δx)−f(x)δx.
Here differentiability is also called it's derivative and limit should exist for the function to be differentiable
We can use above formula to find derivative but by replacing δx by h i.e.
dydx=limh→0f(x+h)−f(x)h
For example , y=sin2x
dydx=limh→0f(x+h)−f(x)h
=limh→0sin2(x+h)−sin2xh
=limh→02cos(2(x+h)+2x2)⋅sin(2(x+h)−2x2)h
=limh→02cos(2x+h)⋅sinhh=2cos2x
Exponential and Logarithmic Functions
Exponential Function samjhne ke liye hum graph consider karte hai. 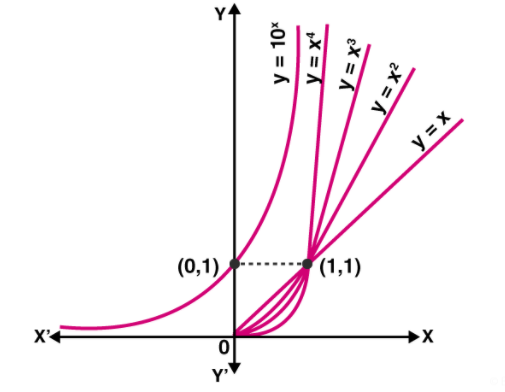
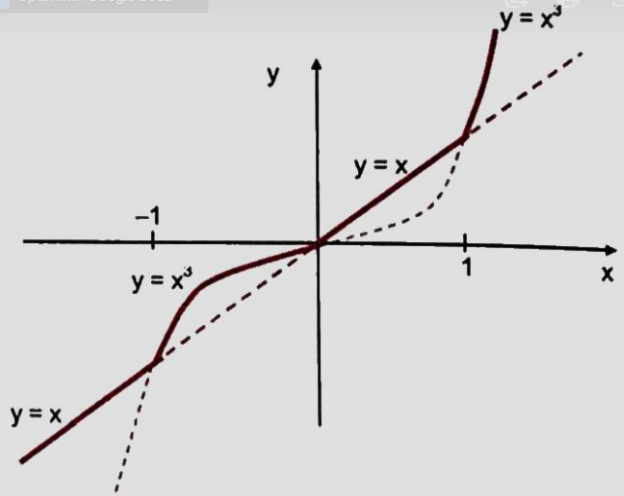
to dekho es figure mein y=x, x2, x3, x4. ka graph hai. Agar hum observe kare to ye curves steeper(sharply) ho rahe hai jse jse x ki power increase kar rahi hai, jitna curve steeper hoga utna hi x ki power increase karegi. Isko hum aise bhi samjh sakte hai ki agar hum x ko replace kar dete hai 10 se so what we would get ? y=100=1, y=101=10, y=102=100, y=103=1000.....so on. To hum dekh sakte hai ki function badi tezi se increase kar rha hai. General form mei essi function ko hum y=bx or y=ex ki form mein express karte hai, inhi sabhi function ko hum exponential function khte hai, jaruri nhi hai ki exponential function ex ki form mei hi express kiya jaye. Jo bhi function es form mei ho jo ki exponentially increase kare unhe hum exponential function kahte hai par dhyan rakha ki exponential function ka base humesha positive rhta hai yani b and e is always greater than 1.
Right hand derivative and Left hand derivative
Right hand derivative at x=a is denoted by , Rf'(a) or f'(a+) and defined as
Rf'(a)=limh→0f(a+h)−f(a)h , h>0
Left hand derivative at x=a is denoted by , Lf'(a) or f'(a−) and defined as
Lf'(a)=limh→0f(a−h)−f(a)−h , h>0
So a function is differentiable only when
Rf'(a) = Lf'(a)
Definition 3
The exponential function with positive base b>1 is the function y=f(x)=bx.
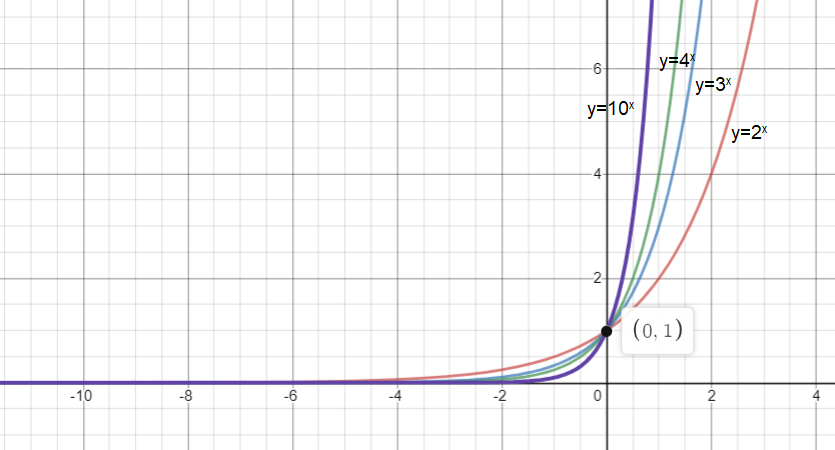
Graph for values of b=2,3,4,10
Observation from graphs :
1. Domain is R, set of all real numbers and Range is set of all positive real numbers.
2. (0,1) always lies on graph.
3. Function is increasing means graph rise when we move from left to right and for large negative value of x function is very close to zero.
4. Function with b=10 is called common exponential function and with b=e is called natural exponential function.
Now we will learn inverse of natural exponential function which called logarithm function.
Example 11
Discuss the differentiability of f(x)=sin|x|
|x| = (xx>0−xx<0)
f(x) = (sinx,x>0) , (sin(−x) , x<0)
f'(x+) = f'(x−)[ For the function to be differentiable ]
f'(0+) = limh→0f(0+h)−f(0)h
= limh→0sinh−0h=1 [L- Hospital's rule ]
f'(0−) = limh→0f(0−h)−f(0)−h
= limh→0−sin(−h)−h=−1
Hence the function is not differentiable
Definition 4
Let b>1 be a real number. Then we say logarithm of a to base b is x if bx=a.
Then Logarithm of a to base b is denoted by logba. Thus, logba=x if bx=a
logx denotes the logarithm function to base e, i.e., lnx will be written as simply logx
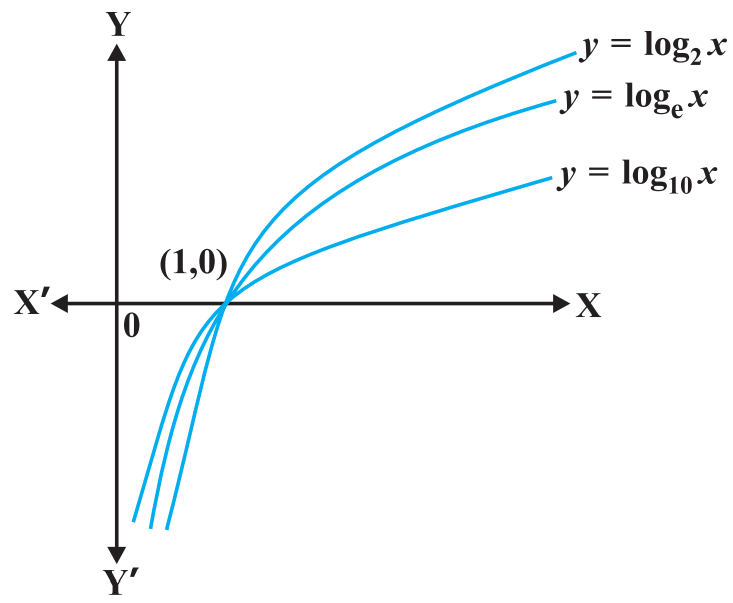
This graph is of logarithm of base 2,e and 10.
Observation from graphs:
1. Domain is positive real numbers and Range is R, real numbers
2. (1,0) always lies on graph.
3. Function is increasing means graph rise when we move from left to right and for value of x near to zero graph approaches y-axis (but never meets it).
4. As we discuss lnx is inverse of ex so both are mirror image in the line y=x.
Example 12
The value of p and q for which the function f(x)=⎡⎢
⎢
⎢
⎢⎣sin(p+1)x+sinxxx<0qx=0√x+x2−√xx3/2x>0⎤⎥
⎥
⎥
⎥⎦
is continuous for all x in R , are :
(1) p=12 , q=−32
(2) p=52 , q=−12
(3) p=−32 , q=12
(4) p=12 , q=32
f(x−)=f(x)=f(x+) ; x∈R
f(0−)=f(0)=f(0+)
f(0−)=limx→0sin(p+1)x+sinxx
=limx→0(p+1)sin(p+1)x(p+1)x+sinxx
=p+1+1=p+2
f(0)=q
f(0+)=limx→0√x+x2−√xx32
=limx→0√1+x−1x
=limx→0(1+x)12−1x
=limx→01+12x−1x=12
f(0−)=f(0)=f(0+)
p+2=q=12
q=12 ; p=−32
option 3 is correct
Some properties of log functions
1. logap=logbplogba
a>o, a≠0, p>0
2. logbpq=logbp+logbq
b>0, b≠0, p,q>0
3. logbpn=nlogbp
4. logb(xy)=logbx−logby
Geometrical representation of Differentiability
So Geometrically dydx=limh→0f(x+h)−f(x)h is called as " slope " of tangent to the graph of y=f(x) at a certain point (x,f(x)) and if there is no tangent at that point than the function is not differentiable i.e. a function cannot be differentiable where a curve has " 2 slopes " at a point or we call it as " Corner point "
Note :Every differentiable function is continuous but it's converse might not be true because if a function is discontinuous than the there will be a break at that point in the graph which means the limit doesn't exist at that point. (As shown in fig)
Theorem 5
(1) The derivative of ex w.r.t., x is ex ; i.e., ddx(ex)=ex
(2) The derivative of logx w.r.t., x is 1x ; i.e., ddx(logx)=1x
Example 13
let f:R→R be a function defined by f(x)=max{x,x3}. The set of values where f(x) is differentiable is:
From the graph of y=x and y=x3
f(x)=⎛⎜
⎜
⎜
⎜⎝−xx≤−1−x3−1≤x≤0x0≤x≤1x3x≥1⎞⎟
⎟
⎟
⎟⎠
Since there is no break in the graph so the function is continuous but at x=−1,0,1 the curve is having corner points. Sof(x) is not differentiable at these points.(See figure)
Example 6
Differentiate each of the following w.r.t. x:
(i) sinx3
(ii) (2x+3)5
(i) Let y=sinx3.
Putting x3=t, we get
y=sintandt=x3
⇒dydx=costanddtdx=3x2
⇒dydx=(dydt×dtdx)
=(cost.3x2)=3x2cost=3x2cosx3.
Hence, ddx(sinx3)=3x2cosx3.
(ii) Let y=(2x+3)5.
Putting (2x+3)=t, we get
y=t5andt=2x+3
⇒dydt=5t4anddtdx=2
⇒dydx=(dydt×dtdx)=10t4=10(2x+3)4.
Example 14
Let f:R→R be a function given by
f(x+y)=f(x)f(y) for all x,y∈R
If f(x)≠0 for all x∈R and f'(0) exists, then f'(x) equals
We have
f(x+y)=f(x)f(y) for all x,y∈R
⇒f(0)=f(0)f(0) [Replacing x and y both by 0]
⇒f(0)(f(0)−1)=0
⇒f(0)−1= [∴f(0)≠0]
⇒f(0)=1
Again
f(x+y)=f(x)f(y) for all x,y∈R
⇒f(x+h)=f(x)f(h) for all x,h∈R
⇒f(x+h)−f(x)=f(x)(f(h)−1)
⇒f(x+h)−f(x)h=f(x)(f(h)−1h)
⇒limh→0f(x+h)−f(x)h=f(x)limh→0f(h)−f(0)h [∴f(0)=1]
⇒f'(x)=f(x)f'(0) for all x∈R
Logarithmic Differentiation`("variable")^"variable"`
So, es section mein hum kuch special functions ko differentiate krna sikhenge jo ki es form mein present hote hai
y=f(x)=[u(x)]v(x)
To hum dekh sakte hai ki u(x) ki power mei v(x) hai to isse solve karne ke liye hum log lenge to base e so, we get
logy=v(x)log[u(x)]
So, by using chain rule differentiating both side to get
1y⋅dydx=v(x)⋅1u(x)⋅u′(x)+v′(x)⋅log[u(x)]
which implies that
dydx=y[v(x)u(x)⋅u′(x)+v′(x)⋅log[u(x)]]
Note : This method is used only when f(x) and u(x) be positive as otherwise their logarithms are not defined.
Example 7
Differentiate xx w.r.t. x.
Let y=xx...(i)
Taking logarithm on both sides of (i), we get
logy=xlogx...(ii)
On differentiating both sides of (ii) w.r.t. x, we get
1ydydx=x.ddx(logx)+logx.ddx(x)
=(x.1x+logx.1)=(1+logx)
⇒dydx=y(1+logx)
⇒dydx=xx(1+logx).
Derivatives of Functions in Parametric Forms
In many situations, a relation expressed between two variables x and y in the form x=f(t), y=g(t) is said to be parametric form with t as a parameter.
Derivative of function can be calculated using chain rule
dydt=dydx⋅dxdt
or dydx=dydtdxdt( whenever dxdt≠0)
Thus dydx=g′(t)f′(t)(asdydt=g′(t)anddxdt=f′(t)) [ provided f′(t)≠0]
Example 8
Find dydx, if x=at2, y=2at.
Given that x=at2, y=2at
So dxdt = 2at and dydt = 2a
Therefore dydx = dydtdxdt = 2a2at = 1t
Second Order Derivatives
Let y=f(x). Then
dydx=f′(x)
If f′(x) is differentiable, we may differentiate (1) again w.r.t. x. Then, the left-hand side becomes ddx(dydx) which is called the second order derivative of y w.r.t. x and is denoted by d2ydx2. The second order derivative of f(x) is denoted by f''(x) or D2y or y'' or y2 if y=f(x)
Similarly we can define higher order derivative such as third order, fourth order, etc by differentiating previous order derivative.
Example 9
Find the second - order derivative of :
(i)x10
(ii)logx
(iii)tan−1x
(i) Let y=x10. Then,
dydx=10x9.
∴d2ydx2=(10×9)x8=90x8.
Hence, d2ydx2(x10)=90x8.
(ii) Let y=logx. Then,
dydx=1x=x−1.
∴d2ydx2=ddx(x−1)=(−1)x(−1)−1=−x−2=−1x2.
Hence, d2dx2(logx)=−1x2.
(iii) Let y=tan−1x. Then,
dydx=1(1+x2)=(1+x2)−1.
∴d2ydx2=ddx(1+x2)−1=(−1)(1+x2)−2.(2x)=−2x(1+x2)2.
Hence, d2dx2{tan−1x}=−2x(1+x2)2.
Mean Value Theorem
Rolle’s Theorem : "Let f:[a,b]→R be continuous on [a,b] and differentiable on (a,b), such that f(a)=f(b), where a and b are some real numbers. Then there exists some c in (a,b) such that f'(c)=0".
Ab hum kuch aise typical differentiable functions ke graphs ko dekhenge jo Rolle's Theorem ki hypothesis ko satisfy kartey hai.
Chalo observe kartey hai slope of tangent ko curve ke various points a aur b ke liye. Hum dono graphs mein dekh saktey hai ki slope of tangent 0 hai cuve mein at least 1
point par. Isse Rolle's Theorem precisely claim karta hai ki slope of tangent graph ke kisi bhi point pe y=f(x) aur kuch nhi balki derivative hai f(x) ka uss point pe.
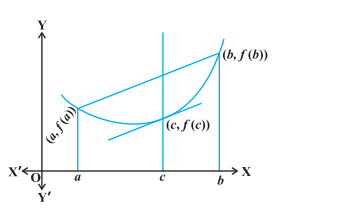
Mean Value Theorem : Let f:[a,b]→R be a continuous function on
[a,b] and differentiable on (a,b). Then there exists some c in (a,b) such that
f'(c)=f(b)−f(a)b−a
Hum ye dekh saktey hai ki MVT Rolle's Theorem ka extension hai. Chalo ab iski geometrical interpretations samjhtey hai. y=f(x) ka graph nichey given hai. Aur humney yah pahley hi explain kar diya hai ki f'(x) slope of tangent to the curve hai y=f(x) at (c,f(c)). Figure se humey yah clear hai ki f(b)−f(a)b−a slope hai secant ke liye jo draw kiya gya hai (a,f(a)) aur (b,f(b)) ke beech. The MVT states that
there is a point c in (a,b) such that the slope of the tangent at (c,f(c)) is same as the slope of the secant between (a,f(a)) and (b,f(b)).
Example 10
Verify Rolle’s theorem for the function y=x2+2, a=–2 and b=2.
The function y=x2+2 is continuous in [–2,2] and differentiable in (–2,2). Also f(–2)=f(2)=6 and hence the value of f(x) at –2 and 2 coincide. Rolle’s theorem states that there is a point c∈(–2,2), where f'(c)=0. Since f'(x)=2x, we get c=0. Thus at c=0, we have f'(c)=0 and c=0∈(–2,2).
Example 11
Verify Mean Value Theorem for the function f(x)=x2 in the interval [2,4].
The function f(x)=x2 is continuous in [2,4] and differentiable in (2,4) as its
derivative f'(x)=2x is defined in (2,4).
Now, f(2)=4 and f(4)=16. Hence
f(b)−f(a)b−a=16−44−2=6
MVT states that there is a point c∈(2,4) such that f'(c)=6. But f'(x)=2x which
implies c=3. Thus at c=3∈(2,4), we have f'(c)=6.
Summary
1. A real valued function is continuous at a point in its domain if the limit of the function at that point equals the value of the function at that point. A function is continuous if it is continuous on the whole of its domain.
2. Sum, difference, product and quotient of continuous functions are continuous if f and g are continuous functions.
3. Every differentiable function is continuous, but the converse is not true.
4. Chain rule is rule to differentiate composites of functions. If f=vou, t=u(x) and if both dtdx and dvdt exist then dfdx=dvdt⋅dtdx.
5. We can obtain derivative by differentiating the whole expression on both side of equality.
6. ddx(sin−1x)=1√1−x2
ddx(cos−1x)=−1√1−x2
ddx(tan−1x)=11+x2
ddx(cosec−1x)=−1x√x2−1
ddx(sec−1x)=1x√x2−1
ddx(cot−1x)=−11+x2
ddx(ex)=ex
ddx(logx)=1x
7. Logarithmic differentiation is a powerful technique to differentiate functions of the form y=f(x)=[u(x)]v(x). Here both f(x) and u(x) need to be positive for
this technique to make sense.
8. dydx=dydtdxdt(wheneverdxdt≠0)
9. d2ydx2=ddx(dydx) which is called the second order derivative of y w.r.t. x
10. Rolle’s Theorem : If f:[a,b]→R is continuous on [a, b] and differentiable
on (a,b) such that f(a)=f(b), then there exists some c in (a,b) such that
f'(c)=0.
11. Mean Value Theorem : If f:[a,b]→R is continuous on [a,b] and differentiable on (a,b). Then there exists some c in (a,b) such that
f'(c)=f(b)−f(a)b−a
Let's Revise
Continuity & Differentiability
- Continuity:
⇒ Geometrically of function at a point : Geometrically hum kah saktey hai ki function y=f(x), x=c par continuous hoga agar us function ka graph y=f(x) continuous (without any break) hoga x=c par.
⇒ Agar left hand limit, right hand limit aur value of the function at x=c, exist aur equal hai ek dusre ke, then function f continuous hoga x=c par.
(a) Function continuous tabhi hoga agar f(c) exist hoga aur agar exist karta hai to f(c) definite, finite aur real hona chahiye.
(b) limx→a exists.
(c) limx→cf(x)=f(c)
⇒ Continuous of a function of in open and closed interval : Koi function f(x) kisi closed interval [a,b] mein tab continuous hoga agar wo continuous ho x ki sari values par jo lie karengi a aur b ke beech mein i.e. to the right of a and to the left of x=b,
limx→af(x)=f(a)
limx→bf(x)=f(b),
aur f(x) ko hum tab continuous kah saktey hai kisi open interval (a,b) mein, agar wo continuous hai (a,b) ke har ek point pe.
Ek real valued function apne domain ke kisi ek point pe tab continuous hoga agar uss function ki limit us point pe equal ho us function ki value ke us point par. Ek function continuous tabhi kahlayega agar wo continuous ho domain ke sare points par.
- Discontinuity of a function :
Koi function tab discontinuous hoga x=c par agar ye cases arise hotey hai,
(a) f(c) is not defined.
(b) limx→c−f(x) aur limx→c+f(x) exist but are not equal.
(c) limx→c−f(x) aur limx→c+f(x) exist and equal but not equal to f(c).
- Differentiability: Suppose karo ek function hai f(x) aur c point hai uske domain mein to derivative f ka c point mein yeh hoga,
f'(c) =limh→0f(c+h)−f(c)h, provided hona chahiye ki ye limit existed ho.
- Operations : Do continuous function ka sum, difference, product ya quotient obtained after division bhi continuous hota hai i.e. agar f aur g continuous functions, hai then
→ (f±g)(x)=f(x)±g(x) is continuous
→ (f.g)(x)=f(x)g(x) is continuous
→ (fg)(x)=f(x)g(x) continuous hai.[note: g(x)≠0]
Hum first order differentiation ko d(f(x))dx ya f'(x) ya y' se represent kartey hai. Aur second order differentiation ko d2(f(x))dx2,f(x), y'', ya y2 se represent kartey hai.
Sarey differentiable function continuous hotey hai magar ye jaruri nhi ki sarey continuous functions bhi differentiable ho.
- Chain Rule : Composite functions ko differentiate karne mein es rule ka use karna padta hai. Agar f=vou aur t=u(x) hai aur dono dtdx aur dvdx exist karta hai tab dfdx=dvdx=dtdx.
- Some key points to remember :
⇒(u±v)'=u'±v'
⇒ Product rule : (uv)'=uv'+u'v.
⇒Quotient rule:(uv)'=u'v−uv'v2.
⇒ Parametric form : If x=f(t) and y=g(t) then dydx=dydtdxdt.
⇒ Chain Rule : y=f(u);u=g(x), then dydx=(dydu)×(dudx).
⇒ddx(xn)=nxn−1.
⇒ddx(sinx)=cosx.
⇒ddx(cosx)=−sinx.
⇒ddx(tanx)=sec2x.
⇒ddx(cotx)=−cosec2x.
⇒ddx(secx)=secxtanx.
⇒ddx(−cosecx)=−cosecxcotx.
⇒ddx(ax)=axlogea
⇒ddx(logx)=1x.
⇒ddx(sin−1)=1√1+x2.
⇒ddx(cos−1x)=−1√1+x2.
⇒ddx(tan−1x)=11+x2.
⇒ddx(cot−1x)=−11+x2.
⇒ddx(sec−1x)=1x√1−x2.
⇒ddx(cosec−1x)=−1x√1−x2.
⇒ddx(ex)=ex.
⇒ddx(logx)=1x.
- Logarithmic differentiation ek bahut powerful technique hai functions ko differentiate karney ka jo iss form mein hotey hai, f(x)=[u(x)]v(x), aur ye condition jaruri hai ki f(x) aur u(x) dono hi +ve ho.