BASIC MATHEMATICS for Class 11 MATHS
Introduction
Hello bachcho, I hope you all are fine. Aaj hum JEE ki teyaari shuru krne vale hai. Aaj hum maths ka first chapter jiska naam hai BASIC MATHEMATICS padhenge. Iss chapter mein hum maths ke basic concepts jo humne abhi tak padhe hai, unn concepts prr discussion karenge. Hum Iss chapter me Number system aur indices ke baare me discussion karne vale hai. Iske sath sath hum, Set theory, Wavy curve Method, Modulus Function ,Exponential and logarithmic functions details mein padhenge aur samjhenge practically questions kis tarha se solve kiye jate hai.. Bachcho ye chapter padhne ke baad aapke sabhi concepts clear ho jayenge aur aap jee ke questions ko easily solve krr lengye. Chalo phir shuru krte hai first chapter ka first topic Number System.
Number System
- Natural numbers :
The counting numbers 1,2,3,4,.... are called Natural Numbers. The set of natural numbers is denoted by N. Thus N={1,2,3,4,....}. - Whole numbers :
Natural numbers including zero are called whole numbers. The set of whole numbers is denoted by W. Thus W={0,1,2,.........}. - Integers : The numbers ...–3,–2,–1,0,1,2,3....are called integers and the set is denoted by I or Z. Thus I(orZ)={..–3,–2,–1,0,1,2,3...}
Note
(a)Positive integers I+={1,2,3....}=N
(b)Negative integers I–={.....,–3,–2,–1}.
(c) Non-negative integers (whole numbers) ={0,1,2,......}.
(d)Non-positive integers ={......,–3,–2,–1,0}. - Even integers :
Integers which are divisible by 2 are called even integers.
Example :0,±2,±4,....... - Odd integers : Integers which are not divisible by ‘2’ are called odd integers.
Example : ±1,±3,±5,±7...... - Prime numbers :
Natural numbers which are divisible by 1 and itself only are called prime numbers.
Example :2,3,5,7,11,13,17,19,23,29,31,........ - Composite number :
Let a be a natural number, a is said to be composite if, it has atleast three distinct factors.
Example : 4,6,8,9,10,12,14,15..........
Note :
(a)1 is neither a prime number nor a composite number.
(b)Numbers which are not prime are composite numbers (except 1).
(c)4 is the smallest composite number.
(d)2 is the only even prime number - Co-prime numbers :Two natural numbers (not necessarily prime) are called coprime, if there H.C.F (Highest common factor) is one.
Example :(1,2),(1,3),(3,4),(3,10),(3,8),(5,6),(7,8)(15,16) etc. These numbers are also called as relatively prime numbers.
Note :(a)Two prime number(s) are always co-prime but converse need not be true.
(b)Consecutive natural numbers are always co-prime numbers. - Twin prime numbers :If the difference between two prime numbers is two, then the numbers are called twin prime numbers.
Example:{3,5},{5,7},{11,13},{17,19},{29,31}
Note :Number between twin prime numbers is divisible by 6 (except (3,5)). - Rational numbers :All the numbers that can be represented in the form pq, where p and q are integers and q≠0, are called rational numbers and their set is denoted by Q. Thus Q={pq:p,q∈Iandq≠0}. It may be noted that every integer is a rational number since it can be written as p1. It may be noted that all recurring decimals are rational numbers.
Note :Maximum number of different decimal digits in pq is equal to q, i.e. 119 will have maximum of 9 different decimal digits. - Irrational numbers :
The numbers which cannot be expressed in pq form where p,q∈I and q≠0 i.e. the numbers which are not rational are called irrational numbers and their set is denoted by Qc . (i.e. complementary set of Q) e.g. 2,1+3 etc. Irrational numbers can not be expressed as recurring decimals.
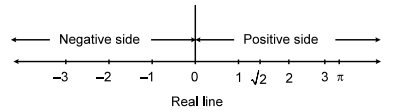
Note : e≈2.71 is called Napier's constant and π≈3.14 are irrational numbers. - Real numbers :
Numbers which can be expressed on number line are called real numbers. The complete set of rational and irrational numbers is the set of real numbers and is denoted by R. Thus R=Q∪Qc .
All real numbers follow the order property i.e. if there are two distinct real numbers a and b then either a<b or a>b.
Note :(a)Integers are rational numbers, but converse need not be true.
(b)Negative of an irrational number is an irrational number.
(c)Sum of a rational number and an irrational number is always an irrational number e.g. 2+3
(d)The product of a non-zero rational number & an irrational number will always be an irrational number.
(e)If a∈Q and b∉Q, then ab= rational number, only if a=0.
(f)Sum, difference, product and quotient of two irrational numbers need not be a irrational number or we can say, result may be a rational number also.
Example 1
If (2200−2192.31+2n) is the perfect square of a natural number , then find the sum of digits of 'n' .
We have given
2200−2192×31+2n.
So we can take 2192 common.
⇒2192[256−31+2k] [taking n−192=k]
Since 2192 is a perfect square.
To bacchon we have to make (225+2k) as a perfect square.
So, we will use hit and trial method.
∴ Let k=1⇒(225+2)=227 which is not a perfect square.
Now, let k=2⇒(225+4)=229 which is still not a perfect square.
Now, let k=6⇒(225+64)=289 which is a perfect square of 17.
So here we got the value of k.
∴K=6
Lakin n−192=k=6
∴n=6+192=198
To bacchon according to the question sum of digits of n=1+9+8=18.
Example 2
Find all 3-digit numbers which are the sums of the cubes of their digits.
Let us suppose the number be xyz.
According to question
xyz=x3+y3+z3.
⇒ Sum of cubes of x,yandz should be xyz.
We know that, smallest 3-digit number is 100=1×100+0×10+0×1
Similarly greatest three digit number will be 999.
To hum yaha kya dekhte hai ki, our range lies between 100−999.
So, the numbers that satisfy this equation is
(i) 153⇒13+53+33=1+125+27=153
(ii) 370⇒33+73+03=27+343+0=370
Similary two more numbers are 371and407.
Example 3
Find the number of natural numbers less than 107 which are exactly divisible by 7.
Let the natural numbers less than 107 be
1,2,3,4,5,.......................106.
To bacchon hume ye pata karna hai ki how many numbers are there which are exactly divisible by 7. Matlab us number ko 7 se divide karne par remainder 0 aana chaiye.
To uske liye humare pas ek formula hai i.e.
Let us suppose our first value be a=1 and last value be an=106.
Let d=7 and n is the required number.
∴an=a+(n−1)d
106=1+(n−1)×7
∴106−1=(n−1)×7
⇒1057=n−1
∴n=15+1=16
So there are 16 such numbers which are divisible be 7.
Example 4
An eight digit number is a multiple of 73 and 137. If the second digit from left is 7, what is the 6th digit from the left of the number ?
We have given 15n2+8n+6n
⇒15n2n+8nn+6n
⇒15n+8+6n
We can see that 15n+8 will always be a natural number for any value of natural number.
Now, for 6n to be natural number, 6 should be completely divisible by n.
∴ possible values of n are 1,2,4and6.
∴ total 4 such numbers are possible.
Example 5
The sum of all values of integers n for which n2−9n−1 is also an integer is
Given n2−9n−1
To bacchon hum ise aise likh sakhte hai
n2−1−8n−1
⇒n2−1n−1−8n−1
⇒(n−1)(n+1)n−1−8n−1
=n+1−8n−1
To bacchon aap yha dekh sakte hai ki kise bhi integer value of n ke liye (n+1) will always be an integer.
Now, for 8n−1 to be an integer 8 should be divisible be |n−1| and jaisa ki hum jante hai divisor of 8 are 1,2,3,4and8
Now if (n−1)>0
n=2,3,5,9
Similarly for (n−1)<0
n=0,−1,−3,and−7.
∴ Sum of all possible values of n=2+3+5+9+0+(−1)+(−3)+(−7)=8
Indices
Indices ka matlab hai ek number apne aap se kitni baar multiply ho sakta hai. Jaise 'a' koi bi ek non zero real or imaginary number hai to the power 'm' where m is a positive integer, a is called the base and m is called the index, m ko hum power or exponent bhi khte hai. Toh chlo ab hum indicies ke kuch Laws ke baare mein padhte hai jo ki humme algebraic expression ko solve krne mein help karenge.
Definition of Indices
If 'a' is any non zero real or imaginary number and 'm' is the positive integer, then am=a.a.a..................a (m times). Here a is called the base and m is called the index, power or exponent.
Laws of Indices :
1. a0=1,(a≠0)
Kabhi bhi kisi bhi constant ki power agar zero hogi to uska result one ke equal aaye ga. Ye kuch matter nahi krta ki base ki kya value kya hai. For Example : - 90=1
2. a−m=1am,(a≠0)
Jab bhi kisi index ki power agar negative hai iska matlab vo iska inverse hai i.e. = 1am
3. am.an=am+n where m and n are rational numbers, (a≠0)
Jab bhi koi do indices multiplication mein ho aur unka base same ho that means unki power add ho jayengi. For Example : - 9−7=197
4. aman=am−n where m and n are rational numbers, (a≠0)
Jab bhi do indices ka base same ho aur vo division mein ho toh unki powers subtract ho jayengi. For Example : - 9492=94−2=92
5. (am)n=amn
Jab bhi kisi base ki power mein raise to power ho toh yeh dono powers result mein multiply ho jayengi. For Example : - (92)3=92.3=96
6. apq=q√ap
agar kisi base ki power fraction me di hai to, isse hum radical form me bi likh sakte hai.
For Example : - 943=((94)3)=3√94
Example 6
a(√a+√b2b√a)−1+b(√a+√b2a√b)−1
=a(2b√a√a+√b)+b(2a√b√a+√b) [because a−1=1a]
=a(2b√a)+b(2a√b)√a+√b
=2ab(√a+√b)√a+√b
=2ab
Example 7
Solve
3√2−2√33√2+2√3+√12√3−√2
We have given 3√2−2√33√2+2√3+√12√3−√2
Now we can rationalize both the terms.
⇒3√2−2√33√2+2√3⋅3√2−2√33√2−2√3+√12√3−√2⋅√3+√2√3+√2
=18+12−12√618−12+2√3(√3+√2)3−2
=30−12√66+6+2√61
=5−2√6+6+2√6
=11.
Example 8
If both a and b are rational numbers, then find a and b.3+√73−√7=a−b√7
We have given 3+√73−√7=a−b√7
Now we can rationalize the L.H.S i.e.
= 3+√73−√7×3+√73+√7
=9+6+6√79−7
=16+6√72
=8+3√7
Ab ise R.H.S ke sath equate and cmpare krenge. i.e.
8+3√7=a−b√7
On comparing a=8 and b=−3.
Example 9
If 143∑k=41√k+√k+1=a−√b then a and b are respectively.
We have given
143∑k=41√k+√k+1=a−√b
Multiplying numerator and denominator by √k+1−√k i.e.
143∑k=4√k+1−√k(√k+√k+1)×(√k+1−√k)
=143∑k=4√k+1−√k√k+1−k
=143∑k=4√k+1−√k1
=143∑k=4[√k+1−√k]
Now expanding the summation
(√5−√4)+(√6−√5)+(√7−√6)........................+(√144−√143)
Now hum yha dekh sakte hai ki bahut sare terms aapas me cancle ho jayenge so finally we have
−√4+√144
=−2+12
=10.
So according to the question 10=a−√b
On comparing L.H.SandR.H.S.
a=10andb=0.
Example 10
(461+462+463+464) is divisible by
(a) 3
(b) 11
(c) 13
(d) 17
We have given (461+462+463+464)
Taking 461 common
=461[1+41+42+43]
=461[1+4+16+64]
=85×461
Now ab hum yha 85 ko factor karke likh sakte hai i.e.
=17×5×461
Yha hum dekh sakte hai ki 17 is a factor which means (461+462+463+464) is divisible by 17.
So the correct option is d.
Example 11
If x+y+z=12andx2+y2+z2=96and1x+1y+1z=36, then the value x3+y3+z3 divisible by prime number is________.
Given (x+y+z)2=144
∴x2+y2+z2+2(xy+yz+zx)=144
⇒96+2(xy+yz+xz)=144 [since x2+y2+z2=96]
∴xy+yz+zx=144−962=24
Given
1x+1y+1z=36
Taking L.C.M
⇒yz+zx+xyxyz=36
∴36xyz=24
xyz=2436=23
Now x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−(xy+yz+zx))
x3+y3+z3−3×(23)=12×[96−24]
∴x3+y3+z3−2=12×72
=x3+y3+z3=864
Now hum ye dekhte hai ki 864 is a even number which can only be divisible by a prime number which is 2.
Definition of Set
A set is a collection of well defined objects which are distinct from each other .
Set are generally denoted by capital letters A,B,C,.................. etc. and the elements of the set by a,b,c........... etc.
If a is an element of a set A, then we write a∈A and say a belongs to A. If a does not belong to A then we write a∉A.
e.g. The collection of first five prime natural numbers is a set containing the elements 2,3,5,7,11.
N = Set of all natural numbers = {1,2,3,4,....}
W = Set of all whole numbers = {0,1,2,3,....}
Z or I set of all integers = {....–3,–2,–1,0,1,2,3,....}.
Methods to write a Set : -
1. Tabulation Method or Roster : In this method a set is described by listing elements, separated by commas and enclose then by curly brackets.
e.g. The set of vowels of English Alphabet may be described as {a,e,i,o,u}
Example : A set of days of week {Sun,Mon,Tues,Wed,Thru}
2. Set builder Method : In this case we write down a property or rule p Which gives us all the element of the set.
Example : If A={1,2,3,4} then in set builder method,
A={x:x∈Nandx≤4} where N is the Set of natural numbers.
Types of Sets
- Null Set or Empty Set : A set having no element in it is called an Empty Set or a null Set or void Set. It is denoted by ϕ or {}.
Example : A={x:x∈Nand5<x<6}=ϕ - Singleton Set : A set consisting of a single element is called a singleton Set.
Example : Then set {0}, is a singleton Set. - Finite Set : - A set which has only finite number of elements is called a finite set.
Example : A = {a, b, c}. - Order of a finite set : - The number of elements in a finite set is called the order of the set A and is denoted by O(A) or n(A). It is also called cardinal number of the set.
Example : A={a,b,c,d}⇒n(A)=4 - Infinite Set : - A set which has an infinite number of elements is called an infinite set.
Example : A = {1, 2, 3, 4, ....} is an infinite set. - Equal Set : - Two sets A and B are said to be equal if every element of A is a member of B, and every element of B is a member of A. If sets A and B are equal. We write A=B and A and B are not equal then A≠B.
Example : A={1,2,6,7} and B={6,1,2,7} ⇒ A=B. - Equivalent Sets : - Two finite sets A and B are equivalent if their number of elements are same i.e. n(A)=n(B).
Example : A={1,3,5,7},B={a,b,c,d}
n(A)=4 and n(B)=4 ⇒ n(A)=n(B)
Note : Equal set always equivalent but equivalent sets may not be equal. - Subset : Let A and B be two sets if every element of A is an element B, then A is called a subset of B if A is a subset of B. we write A⊂B.
Example : A = {1, 2, 3, 4} and B = {1, 2, 3, 4, 5, 6, 7} in A sub B
The symbol ⇒ stands for implies. - Proper subset : If A is a subset of B and A≠B then A is a proper subset of B and we write A⊆B
- Universal set : A set consisting of all possible elements which occur in the discussion is called a Universal Set and is denoted by U
Note-1 : Every set is a subset of itself i.e. A⊆A for all A
Note-2 : Empty set ϕ is a subset of every set
Note-3 : Clearly N⊂W⊂Z⊂Q⊂R⊂C
Note-4 : The total number of subsets of a finite set containing n elements is 2n
Note : All sets are contained in the universal set.
Example : If A={1,2,3},B={2,4,5,6},C={1,3,5,7}thenU={1,2,3,4,5,6,7}canbetakenastheUniversalset.<b><li>PowerSet:<b>LetAbeanyset.Thesetofall⊂sofAiscal≤dpowersetofAandisde¬edbyP(A).<br><b>Examp≤:<b>LetA = {1, 2}thenP(A) = {phi, {1}, {2}, {1, 2}}<li>Twof∈itesetshavemandne≤mentsrespectively.The→talνmberofe≤ments∈thepowersetofthefirstsetis56morethanthe→talνmberofe≤ments∈thepowersetofthesecondsetf∈dthevalueofmandnrespectively.Answer:2^m-2^n=56=2^3.7=2^3(2^3-1)2^m-2^n=2^6-2^3m=6, n=3
Some Operations On Sets
- Union of two sets(U):
A∪B={x:x∈Aorx∈B}
e.g. A={1,2,3},B={2,3,4} then A∪B={1,2,3,4} - Intersection of two sets :
A∩B={x:x∈Aandx∈B}
e.g. A={1,2,3,},B={2,3,4} then A∩B={2,3} - Difference of two sets :
A–B={x:x∈Aandx∉B}
e.g. A={1,2,3},B={2,3,4};A–B={1} - Complement of a sets:
A'={x;x∉Aandx∈U}=U−A
e.g. U={1,2,....,10},<br>A={1,2,3,4,5}
then A={6,7,8,9,10} - De-Morgan Laws :
(A∪B)'=A'∩B'
(A∩B)'=A'∪B' - A–(B∪C)=(A–B)∩(A–C)
A–(B∩C)=(A–B)∪(A–C) - Distributive Laws :
A∪(B∩C)=(A∪B)∩(A∪C)
A∩(B∪C)=(A∩B)∪(A∩C) - Commutative Laws :
A∪B=B∪A
A∩B=B∩A - Associative Laws:
(A∪B)∪C=A∪(B∪C)
(A∩B)∩C=A∩(B∩C) - A∩ϕ=ϕ;A∩U=A
A∪ϕ=A;A∪U=U - Disjoint Sets :
If A∩B=ϕ, then A,B are disjoint.
e.g. if A={1,2,3},B={7,8,9} then A∩B=ϕ
Note : A∩A'=ϕ therefore A,A' are disjoint - Symmetric Difference of Sets :
A△B=(A–B)∪(B–A)
=(A∪B)−(A∩B)
Example 12
Let R be the real line. Consider the following subsets of the plane R×R.
S={(x,y):y=x+1 and 0<x<2},
T={(x,y):x−y is an integer }.
Which one of the following is true ?
a. Neither S not T is an equivalence relation on R.
b. Both S and T are equivalence relations on R.
c. S is an equivalence relation on R but T is not.
d. T is an equivalence
relation on R but S is not.
y=x+1
∴y<3
Let S is symmetric
So (x,y)∈R<br>(y,x)∈R
but (y,x) is not satisfying 0<x<2
So S is not an equivalence relation.(for verification take y=2 and x=1)
T(x,y)=x−y is integer
(x,x) is an integer always
If (x,y)∈R, then y−x is also an integer.
∵(y,x)∈IR
If (x,y)∈IR&(y,z)∈IR, then (x−y) is an integer, (y−z) is an integer, sum of x−y & y−z=x−z is also an integer.
Hence T is equivalence relation. Option (d) is correct.
Example 13
Let R be the real line. Consider the following subsets of the plane R×R.
S={(x,y):y=x+1 and 0<x<2},
T={(x,y):x−y is an integer }.
Which one of the following is true ?
a. Neither S not T is an equivalence relation on R.
b. Both S and T are equivalence relations on R.
c. S is an equivalence relation on R but T is not.
d. T is an equivalence
relation on R but S is not.
y=x+1
∴y<3
Let S is symmetric
So (x,y)∈R<br>(y,x)∈R
but (y,x) is not satisfying 0<x<2
So S is not an equivalence relation.(for verification take y=2 and x=1)
T(x,y)=x−y is integer
(x,x) is an integer always
If (x,y)∈R, then y−x is also an integer.
∵(y,x)∈IR
If (x,y)∈IR&(y,z)∈IR, then (x−y) is an integer, (y−z) is an integer, sum of x−y & y−z=x−z is also an integer.
Hence T is equivalence relation. Option (d) is correct.
Example 14
If A, B and C are three sets such that A∩B=A∩C and A∪B=A∪C, then
a.A=B b.A=C
c.B=C d.A∩B=ϕ
Let x∈C
Suppose x∈A⇒x∈A∩C
⇒x∈A∩B (∵A∩C=A∩B)
Thus x∈B
Again suppose x∉A⇒x∈C∪A
⇒x∈B∪A⇒x∈B
Hence C⊆B ...(1)
Similarly we can show that B⊆C ...(2)
Combining (1) and (2) we get B=C.
Option (c) is correct.
Example 15
Let R be the set of real numbers.
Statement 1:A={(x,y)∈R×R:y−x is an integer} is an equivalence relation on R.
Statement 2:B={(x,y)∈R×R:x=αy for some rational number alpha} is an equivalence relation on R.
a. Statement 1 is false, statement 2 is true
b. Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
c. Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
d. Statement 1 is true, statement 2 is false
y−x is an integer
x−x=0 is also an integer
∴A is reflexive
x−y is also an integer.
Hence, it is symmetric.
For (x,y)∈R×R and (y,z)∈R×R. y−x and z−y are both integers, then sum of them is also an integer.
Hence, transitive.
If a set is symmetric, transitive and reflexive then it also has equivalence relation.
Clearly, A is an equivalence relation
Now B,
xy=α is rational but
yx need not be rational i.e. 01 is rational but
10 is not rational.
Hence, B doesn't show equivalence relationship.
Correct option is (d) statement 1 is true, statement 2 is false.
Example 16
Let S be a non-empty subset of R. Consider the following statement :
P:
There is a rational number x∈S such that x>0.
Which of the following statements is the negation of the statement P?
a. x∈S and x≤0⇒x is not rational.
b. There is a rational number x∈S such that x≤0.
c. There is no rational number x∈S such that x≤0
d. Every rational number x∈S satisfies x≤0.
P: there is a rational number x∈S such that x>0
∼P: Every rational number x∈S satisfies x≤0
Hence, option (d) is correct.
Example 17
A function f from the set of natural numbers to integers defined by
f(n)=n−12, when n is odd
=−n2, when n is even
is
a. one-one but not onto
b. onto but not one-one
c. one-one and onto both
d. neither one-one nor onto
One-One test for f:
Let x1 and x2 be any two elements in the domain (N).
Case I : When both x1 and x2 are even.
Let f(x1)=f(x2)
⇒−x12=−x22
⇒−x1=−x2
⇒x1=x2
Case II : When both x1 and x2 are odd.
Let f(x1)=f(x2)
⇒x1−12=x2−12
⇒x1=x2
From, all cases, we can say that f is one-one
Onto test of f :
Codomain of f=Z={...,−3,−2,−1,0,1,2,3,...}
Range of f={...,−2−12,−−22,−1−12,02,1−12,−22,3−12,...}
Range of f={...,−2,1,−1,0,0,−1,1,...}
⇒ Co-domain of f= Range of f
Or we can say that since, each negative integer is an image of even natural number and positive integer is an image of odd natural number.
∴f is onto.
Option (c) is correct.
Venn diagram
A Venn diagram is a graphical representation of the elements in a set or a group. It is a diagram that shows all the possible logical relationships between sets or groups. In Venn diagrams, the elements of the sets are written in their respective circles.
In below figure U={1,2,3,...,10} is the universal set of which A={2,4,6,8,10} and B={4,6} are subsets, and also B⊂A.

Example 18
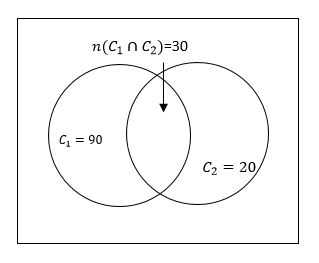
There are 200 individuals with a skin disorder, 120 had been exposed to the chemical C1? 50 to chemical C2, and 30 to both the chemicals C1and C2. Find the number of individuals exposed to(i) Chemical C1but not chemical C2
By using venn diagram
(i) 90
Wavy Curve Method
The wavy curve method is used for solving inequalities in the form f(x)=(x−a1)n1(x−a2)n2…….(x−ak)n=k(x−b1)m1(x−b2)m2…..(x−bp)mp>0(<0,=<0,or⇒0) where n1,n2,....,nk,m1,m2,....,mp are natural numbers and the numbers a1,a2,…..,ak;b1,b2,.....,bp are any real numbers such that a i b j, where i=1,2,3,……,k and j=1,2,3,……,p.The wavy curve method is also called the method of intervals.
Rules
- Firstly we have to simplify and factorize inequality
- Make sure, the coefficient of x is/are positive
- Then, find all the critical points
- Put + sign for right most places and alternatively change sign as move towards left on the number line
Example 19
If (y2−5y+3)(x2+x+1)<2x for all x∈R, then find the interval in which y lies.
We have, (y2−5y+3)(x2+x+2)<2x,∀x∈R
⇒y2−5y+3<2xx2+x+1 (because x2+x+1>0∀x∈R)
L.H.S. must be less then least value of R.H.S. Now let's find the range of R.H.S
Let 2xx2+x+1=p
or px2+(p−2)x+p=0
Since x is real, we have
(p−2)2−4p2≥0
or −2≤p≤23
The minimum value of 2xx2+x+1 is −2. So,
y2−5y+3<−2
⇒y2−5y+3<0
⇒y∈(5−√52,5+√52)
Example 20
Find the values of k for which ∣∣∣x2+kx+1x2+x+1∣∣∣<2,∀x∈R
We have
|x|<a⇒−a<x<+a
∴ The given inequality implies
−2<x2+kx+1x2+x+1<2 ...(1)
Now, x2+x+1=(x+12)2+(34) is +ve for all values of x.
Multiplying (1) by x2+x+1, we get
−2(x2+x+1)<x2+kx+1<2(x2+x+1)
This yields two inequalities, viz.,
3x2+(2+k)x+3)>0
and x2+(2−k)x+1<0
For above inequalities to be true for all values of x, their discriminants must be negative. Hence,
(2+k)2−36<0 and (2−k)2−4<0
⇒(k+8)(k−4)<0andk(k−4)<0
⇒−8<k<4and0<k<4
Therefore, 0<k<4.
Example 21
Solve the following inequality
x4−3x3+2x2x2−x−30>0
We have, x4−3x3+2x2x2−x−30>0
⇒(x2)(x2−3x+2)x2−x−30>0
On factorizing both numerator and denominator we get,
x2(x−1)(x−2)(x+5)(x−6)>0
Our inequality becomes +ve when x∈(6,∞), -ve when x∈(2,6), +ve when x∈(1,2), -ve when x∈(−5,1) and +ve when (−∞,−5)
So, we can conclude that the required result is x∈(−∞,−5)∪(1,2)∪(6,∞).
Example 22
Complete the solution of inequality (x+2)(x+3)(x−2)(x−3)≤1 is
We have,
(x+2)(x+3)(x−2)(x−3)−1≤0
⇒(x+2)(x+3)−(x−2)(x−3)(x−2)(x−3)≤0
⇒10x(x−2)(x−3)≤0
From the above inequality we came to know that it is positive when x∈(3,∞), negative when x∈(2,3), positive when x∈[0,2) and negative when x∈(−∞,0].
So we conclude that for the above given inequality x∈(−∞,0]∪(2,3).
Note : We have to avoid cross multiplying to get rid of mistakes.
Example 23
If a>0andb2−4ac=0, then solve ax3+(a+b)x2+(b+c)x+c>0.
We have,
ax3+(a+b)x2+(b+c)x+c>0
⇒ax2(x+1)+bx(x+1)+c(x+1)>0
⇒(x+1)(ax2+bx+c)>0
⇒a(x+1)(x+b2a)2>0 as b2−4ac=0
⇒x>−1andx≠−b2a
Modulus Function
A modulus function is a function which gives the absolute value of a number or variable. Ye function result me hamesha variables ka magnitude btayega. Modulus function ko absolute value function bi kehte hai. Iss function ka result always positive rhega. Input ki value positive ho ya negative isse result me koi fark nahi prdega.
The modulus function f(x) of x is defined as: f(x)=|x|
Or
y=|x|; Where f:R→R and x∈R; And |x| states modulus or mod of x.
If x is positive then the output of the function f(x) will be x only. But if x is negative, then the output of x will be the magnitude of x. Hence, Hum modulus function ko iss terh se bi define krr sakte hai: f(x)={xx≥0−xx<0
Therefore, if the value of x is greater or equal to 0, then the modulus function takes the actual value. But if the value of x is less than 0, then the function takes minus of the actual values.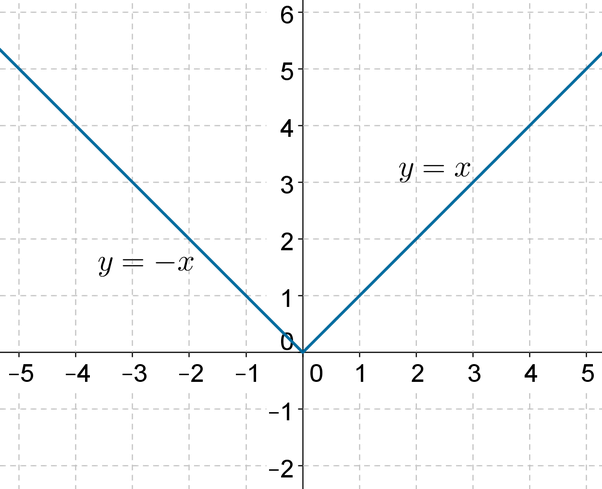
Example 24
The set of real values of x satisfying ||x−1|−1|≤1, is
(i) [−1,3]
(ii) [0,2]
(iii) [−1,1]
(iv) none of these
Since x-1 changes its sign as x passes through 1.
So, following cases arise.
CASE I When x<1
In this case, we have |x−1|=−(x−1)
∴||x−1|−1|≤1
⇒|−(x−1)−1|≤1
⇒|−x|≤1
⇒|x|≤1
⇒−1≤x≤1 [∵|x|≤a⇔−a≤x≤a]
⇒−1≤x<1 [∵x<1]
∴x∈[−1,1])
CASE II When x≥1
In this case, we have |x-1| = x -1
∴||x−1|−1|≤1
⇒|x−1−1|≤1
⇒|x−2|≤1⇒2−1≤x≤2+1⇒x∈[1,3]
Hence, x∈[−1,3]
Example 25
Solve log2|x−1|<1
log2|x−1|<1
⇒|x−1|<21
⇒|x−1|<2
Case 1: When x≥1,
Then, x−1<2
⇒x<3
∴x∈[1,3)
Case 2: When x≤1,
Then, −x+1<2
⇒−x<1
⇒x>−1
∴x∈(−1,1]
So, common solution for these two cases will be,
x∈(−1,3).
Example 26
Solve 1≤|x−2|≤3.
Given 1≤|x−2|≤3
Taking x≥2
we have 1≤x−2≤3
adding 2 both sides
1+2≤x−2+2≤3+2
⇒3≤x≤5
∴x∈[3,5]
Now if x<2
So, 1≤−(x−2)≤3
multiplying inequality with negative sign
we have, −3≤x−2≤−1
Adding 2 on both sides
∴−3+2≤x−2+2≤−1+2
⇒−1≤x≤1
x∈[−1,1]
Ab hum dono cases ka union lenge i.e.
x∈[−1,1]∪[3,5]
Example 27
Solve : ∣∣x2−x∣∣+|x+1|=5,x∈R
Given ∣∣x2−x∣∣+|x+1|=5
Here we will have to check for different cases i.e.
Case 1
x≥1
Mods will open with positive sign
∴x2−x+x+1=5
x2=4
⇒x=+2,−2
According to range x=2
Case 2
0≤x<1
first mod will open with negative sign and second mod will open with positive sign.
∴x−x2+x+1=5
x2−2x+4=0
Here D<0
∴ No Solution .
Case 3
−1≤x≤0
Both mod will open with positive sign
but x=+2,−2
Range me na +2 lie karta hai na hi −2. So no solution
Case 4
x≤−1
second mod will open with negative sign
x2−x−x−1=5
x2−2x−6=0
D=28
∴x=2−√282
Finally we have the values of x i.e.
x=(1−√7),2
Example 28
The product of all the solutions of the equation(x−2)2−3|x−2|+2=0 is
Case 1
When x≥2
(x−2)2−3(x−2)+2=0
let x−2=t
Now, t2−3t+2=0
Now splitting the middle term i.e.
t2−2t−t+2
⇒t(t−2)−1(t−2)
⇒(t−1)(t−2)
∴t=1,2
Now if t=1
So, x=1+2=3
Similarly if t=2
x−2=2<br>:x−4
Case 2
when x<2
Our equation will be of the form
(x−2)2+3(x−2)+2=0
or, t2+3t+2=0
⇒t2+3t+2t+2=0
⇒t(t+2)+1(t+2)
⇒(t+1)(t+2)=0
∴t=−1,−2
if t=−1
x−2=−1
∴x=1
Similarly if t=−2
x−2=−2
⇒x=0
Now the product =3×4×1×0=0
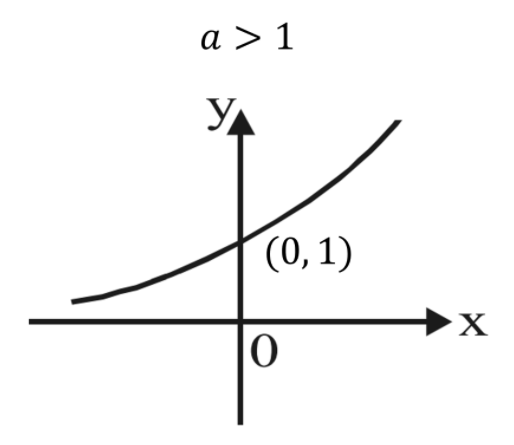
Exponential Function : -
An exponential function is a function which is in the form f(x)=ax=exIna(a>0,a≠1,x∈R), where x is a variable and a is a constant which is called the base of the function and it should be greater than 0. The exponential curve depends on the exponential function and it depends on the value of the x. Where a>0 and a is not equal to 1.;x is any real number.; If the variable is negative, the function is undefined for −1<x<1
Logarithmic Function : -
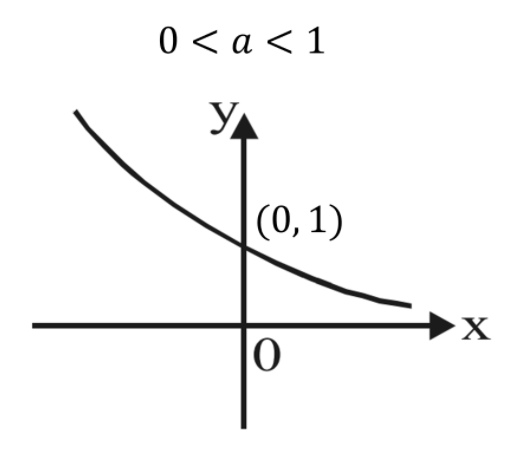
Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y=ax is x=ay. The logarithmic function y=loga(x) is defined to be equivalent to the exponential equation x=ay.
y=loga(x) only under the following conditions: x=ay,a>0, and a≠1. It is called the logarithmic function with base a.
By definition, aloga(x)=xfor every real x>0.Below are pictured graphs of the form y=loga(x) when a>1 and when 0<a<1. Notice that the domain consists only of the positive real numbers, and that the function always increases as x increases.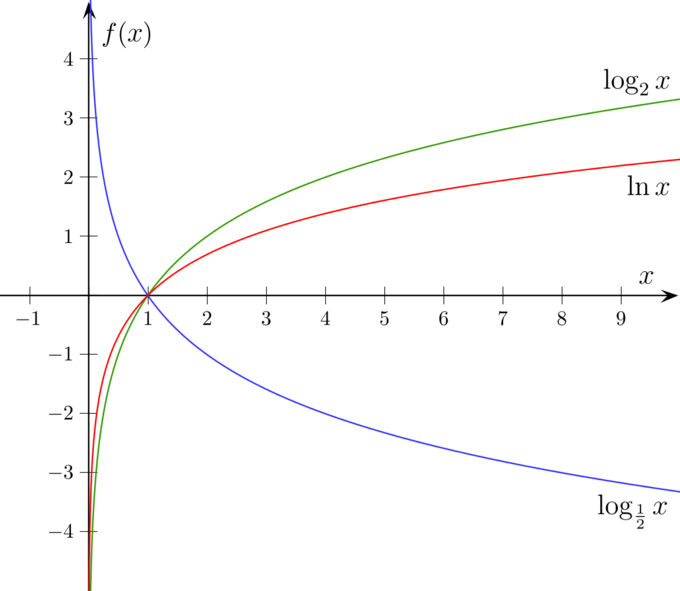
Properties of Logarithms Function : -
Example 29
Let (xo,yo) be the solution of the following equations
(2x)ln2=(3y)ln3
3lnx=2lny, then xo is
We have,
(2x)ln2=(3y)ln3
⇒ln2(ln2+lnx)=ln3(ln3+lny) ...(1)
And, 3lnx=2lny
⇒lnxln3=lnyln2 ...(ii)
From (i) and (ii), we get
⇒ln2(ln2+lnx)=ln3(ln3+(lnxln3ln2))
⇒ln22−ln33=lnx{ln23ln2−ln2}
⇒lnx=−ln2
⇒x=12
Example 30
If 3x=4x−1, then x=
(a)2log322log32−1 (b)22−log23
(c)11−log43 (d)2log232log23−1
We have, 3x=4x−1
Take log on both sides with base a
xloga3=(x−1)loga4⇒x=loga4loga4−loga3
If a=3:x=2log322log32−1
If a=2:x=22−log23
If a=4:x=11−log43
Hence option a,b and c are correct.
Example 31
The value of 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2... is
Let y=
⎷4−13√2
⎷4−13√2√4−13√2...
y2=4−13√2y⇒3√2y2=12√2−y
⇒3√2y2+y−12√2=0
⇒(3y−4√2)(√2y+3)=0
⇒y=4√23;y=−3√2(rejected)
∴V=6+log32(13√2y)
=6+log32(13√2⋅4√23)=6+log32(23)2
=6−2=4
Example 32
If the sum of 1+1+22+1+2+33+... to n terms is S, then S is equal to
Let Tn be the nth term of the given series.
Thus, we have :
Tn=1+2+3+4+...+nn=n(n+1)2n=n2+12
Now, let
Sn be the sum of n terms of the given series
Thus, we have
Sn=n∑k=1(k2+12)
⇒Sn=n∑k=1k2+12
⇒Sn=n(n+1)4+n2
⇒Sn=n2(n+12+1)
⇒Sn=n2(n+32)
⇒Sn=n(n+3)4
Example 33
If n is a multiple of 3, then the coefficient of xn in the expansion of loge(1+x2+x),|x|<1 is
Since 1+x+x2=1−x31−x for |x|<1, we have loge(1+x+x2)=loge(1−x31−x)=loge(1−x3)−loge(1−x)
Also loge(1−x)=−[x+x22+x33+...] and hence loge(1−x3)=−[x3+x62+x93+...]
∴loge(1−x3)−loge(1−x)=−[x3+x62+x93+...]+[x+x22+x33+...]
Simplify the R.H.S.
loge(1−x3)−loge(1−x)=loge(1+x+x2)=x+x22−2x33+x44+x55−2x66+x77+...
Hence for n multiple of 3, we get an=−2n.