AREAS RELATED TO CIRCLES for Class 10 MATHS
Introduction
Hello bachho, aap sab simple figures ka perimeter aur area nikalna to jante hi hai such as rectangles, squares, parallelogram, triangles and circles ye sab nikalna to apne apni phichli classes mei shikha hi hai. Bachho bahut sare ase objects hote hai joki hum dekhte hai apni daily life mei circles se related hoti hai somehow. For ex.- Cycle wheels, wheel barrow ( thela ), round cake, papad, bangles etc. 
Aur inhe hum apni day-to-day life mein use karte hai yani area related to circles ki problems hmare liye practically important hai. To es chapter mei hum circle ke perimeter yani circumference ke concept ko revise karenge aur area of circles ki knowledge ka use karenge to find the area of two special 'parts' of a circular region known as sector and segment.
Perimeter and Area of a Circle — A Review
To dekho bachho agar mein apko kahu ki apko ek circular park ki fencing karni hai to aap kya karenge? So, fencing karne ke liye sabse pehle apko uska area aur cost nikalna hoga. To aap recall kare ek circular path mei jo hum distance cover karte hai vo uska perimeter hota hai jishe circumference of a circle bhi kha jata hai. Aap ye bhi jante hi honge apni pechli classes se that circumference of a circle is a constant ratio with its diameter. Aur ye constant ratio denote kiya jata hai Greek letter π se.
circumferencediameter=π
or, circumference=π×diameter
= π×2r ( where r is the radius of the circle )
=2πr
The great Indian mathematician Aryabhatta gave an approximate value of π. He stated that value of π=227 or 3.14 approximately.
To aapko ye bhi yaad hoga area of circle is πr2, where r is radius of circle.
Esi tarha se agar hum circle ka half karde i.e. a semicircle, so area of semicircle = 12 πr2 and its perimeter is 12 (πd)+d or (πr+2r). Aur agar hum circle ka 14 th part consider kare i.e. its quadrant, so area of quadrant = 14 πr2 and its perimeter is (π2+2)r.
To chalo ek activity perform karte hai ek circle ko given sectors mein cut karte hai then unhe hum rearrange karte hai jsa es fig. mein given hai. 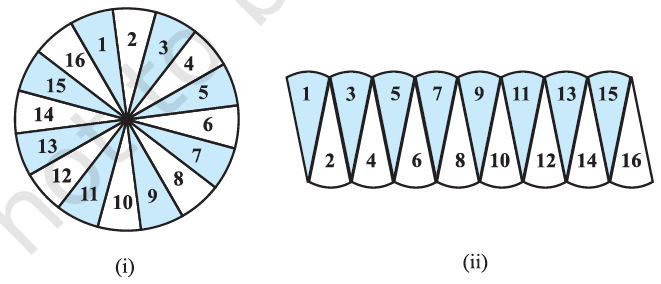
To aapne notice kiya jo shape humne rearrange karke bnayi hai nearly ek rectangle hai of length 12×2πr and breadth r. This suggest area of circle = 12×2πr×r=πr2.
Example 1
The cost of fencing a circular field at the rate of Rs.25 per metre is Rs. 5500. The field is to be ploughed at the rate of 50 paise per m2. Find the cost of ploughing the field. [Take π=227]
Rate of fencing =Rs.25 per metre. Cost of fencing =Rs.5500
Perimeter =total costrate/metre=(550025)m=220m
Let R be the radius of the field. Then,
2πR=220⇒2×227×R=220⇒R=(220×744)m=35m
area of the field =πR2=(227×35×35)=3850m2
Cost of ploughing at 50 Paise per m2=Rs.(3850×50100)=Rs.1925
Example 2
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has its circumference equal to the sum of the circumferences of the two circles.
Given that r1=19,r2=9,r3=?
Acc to question,
2π(r3)=2π(r2)+2π(r1)
cancel(2 pi) (r_3) = cancel( 2 pi )(r_2+r_1)
r3=r2+r1
r3=9+19cm
=28cm
This is the required answer.
Example 3
The wheel of a motor cycle is of radius 35cm. How many revolutions per minute must the wheel make, so as to keep a speed of 66 (km/h) ?
Given, radius of wheel, r=35cm
Circumference of the wheel = 2πr
= 2×227×35
=220cm
But speed of the wheel = 66kmh−1=66×100060m/min
= 1100×100cm−1min
= 110000cm−1min
∴ Number of revolutions in 1 min = 110000220=500 revolution
Hence, required number of revolutions per minute is 500.
Areas of Sector and Segment of a Circle
To bachho aap sabne sector aur segment of a circle to suna hi hoga apni pichli classes se. To kya apko yaad hai circuclar region ka vo part jo ki do radii se enclosed hokar banta hai like a piece of cake is called the sector of the circle. 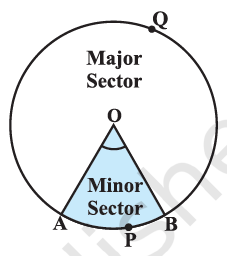
Es figure mein shaded region OAPB sector hai circle ka with centre O. ∠AOB is called the angle of the sector and the unshaded region OAQB is also called the sector of the circle.
Note→ In this figure, OAPB is called the minor sector and OAQB is called the major sector. You can also see that the angle of the major sector is 360∘−∠AOB.
Ab es figure mein dekho AB chord hai circle ka with centre O. So, students shaded region APB segment hua circle ka aur AQB unshaded region bhi ek segment hua formed by chord AB.
Note→ APB is called the minor segment and AQB is called the major segment.
Remark : When we write segment and sector we will mean the minor segment and the minor sector respectively, unless stated otherwise.
Derivation
Area of the sector of angle θ = θ360×πr2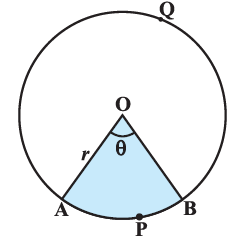
In a circle with centre O and radius r, let OAPB be a sector and θ (in degrees) be the angle of the sector.
Area of the circular region is πr2.
Let this region be a sector forming an angle of 360∘ at the centre O.
Then, the area of a sector of circle formula is calculated using the unitary method.
[Circle Formula → Diameter of a Circle = 2r
Circumference of a Circle = 2πr
Area of a Circle = πr2]
When the angle at the centre is 360∘, area of the sector, i.e., the complete circle = πr2.
When the angle at the center is 1∘, area of the sector = πr2360∘
Thus, when the angle is θ, area of sector, OAPB = θ360∘×πr2
Arc- A part of a curve lying on the circumference of a circle.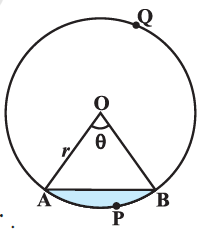
Length of an arc of a sector- The length of an arc is given as :-
θ360∘×2πr
Now let us take the case of the area of the
segment APB of a circle with centre O and radius r (see Fig.). You can see that :
Area of the segment APB = Area of the sector OAPB – Area of △OAB
= θ360×πr2 - area of △OAB
Area of the major sector OAQB = πr2 – Area of the minor sector OAPB
and Area of major segment AQB = πr2 – Area of the minor segment APB
Example 4
Find the area of the sector of a circle with radius 4cm and of angle 30∘. Also, find the area of the corresponding major sector. [Use π=3.14 ]
Area of sector =θ360×πr2
=30360×3.14×42
=112×3.14×16=12.563=4.186cm2
now, area of major sector =π×r2−4.186cm2
=3.14×16−4.186
=50.24−4.186
=46.054cm2
Example 5
In a circle a radius 21cm. An arc subtends an angle 60∘ at the centre:-
(i) the length of an arc
(ii) area of the sector formed by the arc
(iii) the area of the segment made by this arc
(iv) the area of major segment.
Let ACB be the given are subtending an angle of 60∘ at the centre. Then r=21 cm and θ=60∘
(i) Length of the arc ACB=2πrθ360∘cm
=(2×227×21×60∘360∘)cm

=22cm
(ii) Area of the sector OACBO=πr2θ360∘cm2
=(227×21×21×60∘360∘)cm2
=231cm2
(iii) Area of the minor segment ACBA
= (area of the sector OACB) − (area of the ΔOAB)
=(231−12r2sinθ)cm2<br≥[231−(12×21×21×sin60∘)]cm2
=(231−12×21×21×√32)cm2
=(231−14×441×1.72)cm2
=(231−189.63)cm2=41.37cm2
(iv) Area of the major segment BDAB
= (area of the circle) − (area of the minor segment)
={(227×21×21)−41.37}cm2
(1386−41.37)cm2=1344.63cm2
Example 6
An umbrella has 8 ribs which are equally spaced (as shown in the figure).Assuming the umbrella to be a flat circle of radius 42cm.
Find the area between the two consecutive ribs of the umbrella.

Since the ribs are equall spaced, so the angle by two consecutive ribs at the centre =(3609)∘=45∘
Area between two consecutive ribs
= area of a sector of a circle with r=42cm and θ=45∘
=(45360×227×42×42)cm2
=693cm2
Example 7
A round table cover has six and equal designs, as shown in the figure. If the radius of the cover is 28cm find the cost of making the desings, at the rate of Rs. 0.35 per cm2. [ Use √3=1.7]
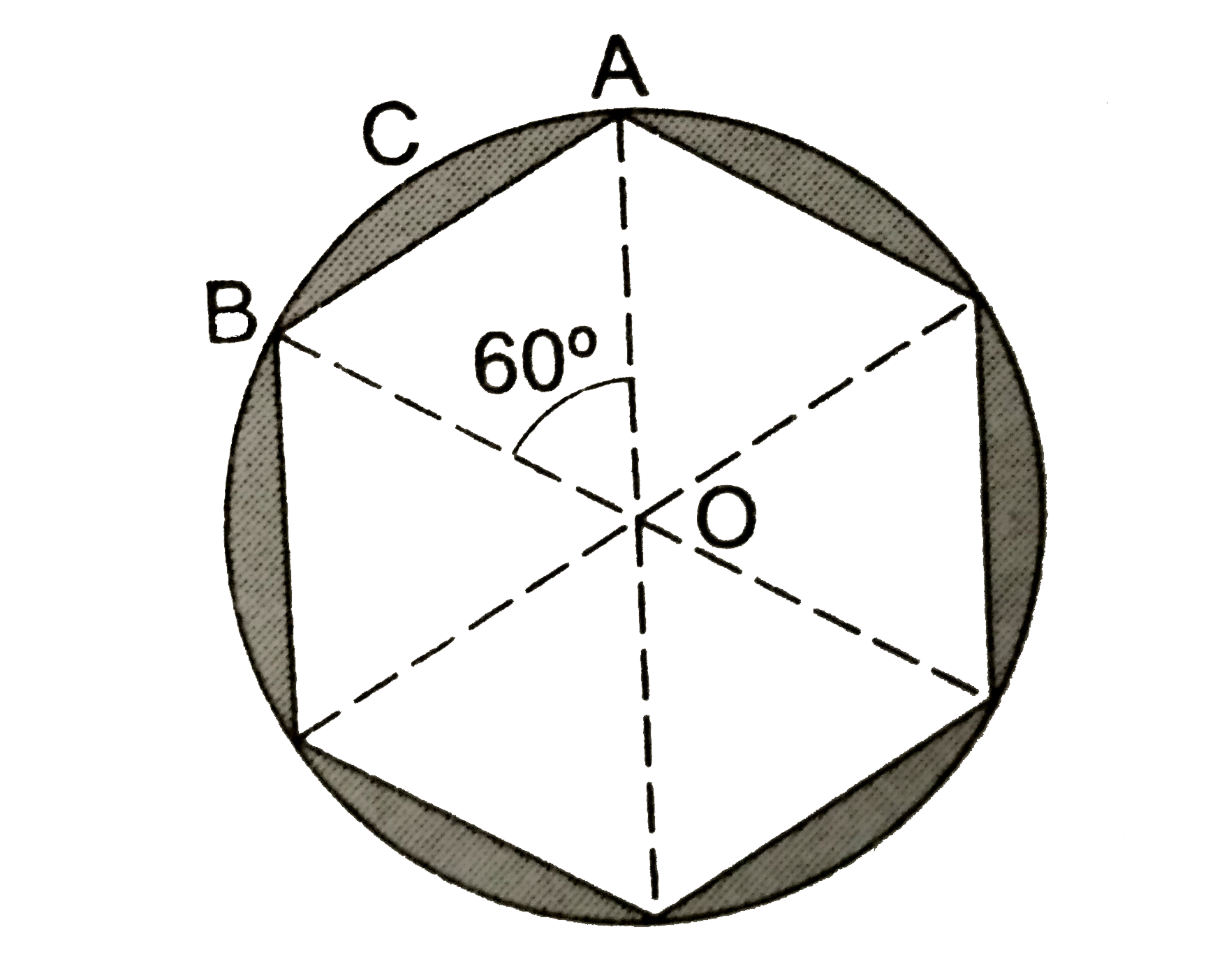
Let O be the centre of the table cover and let it be divide into six equal desings each being a segment. Let one of these segments be ACBA. Clearly ∠AOB=(3606)∘=60∘
ar (segment ACBA) = ar (sector OACBO) − ar(equilateral ΔOAB)
=(πr2θ360−√34a2)
=[(227×28×28×60360)−(√34×28×28)]cm2
[∵a=OA=28cm]
=(12323−1710×7×28)cm2
=(12323−16665)cm2
=(6160−4998)15cm2
=116215cm2
ar (all the six segments)=(116215×6)cm2=23245cm2
Cost of designs =Rs.(23245×35100)=Rs.162.68
Areas of Combinations of Plane Figures
To bachho, abhi tak humne bahut sari figures ka alag alag area nikala hai so ab hum koshish karenge do figures ke combination ka area nikalne ki. Kuch asi figures jinke across hum apni day-to-day life mein ate hai kuch interesting designs like flower beds, drain covers, window designs, designs on table covers, are some of such examples. We illustrate the process of calculating areas of these figures through some examples.
Example 8
In the given figure, ABCD is a square of side 10cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region.
[ Use π=3.14]

Let us mark the unshaded regions as I,II,III and IV as show in the given figure.
Let these regions meet at a common point O. Then,
(area of I) + (area of III)
= ar(sq ABCD) − {ar(semicircle AOD) + ar(semicircle BOC)}
={(10×10)−(12×3.14×52+12×3.14×52)}cm2
=(100−78.5)cm2=21.5cm2
Similarly, (area of II) + (area of IV) =21.5cm2
Area of shade regioin = ar (sq ABCD) − ar((I+II+III+IV)
={(10×10)−(2×21.5)}cm2
=(100−43)cm2
=57cm2
Example 9
Find the area of the shaded region of the figure given below.
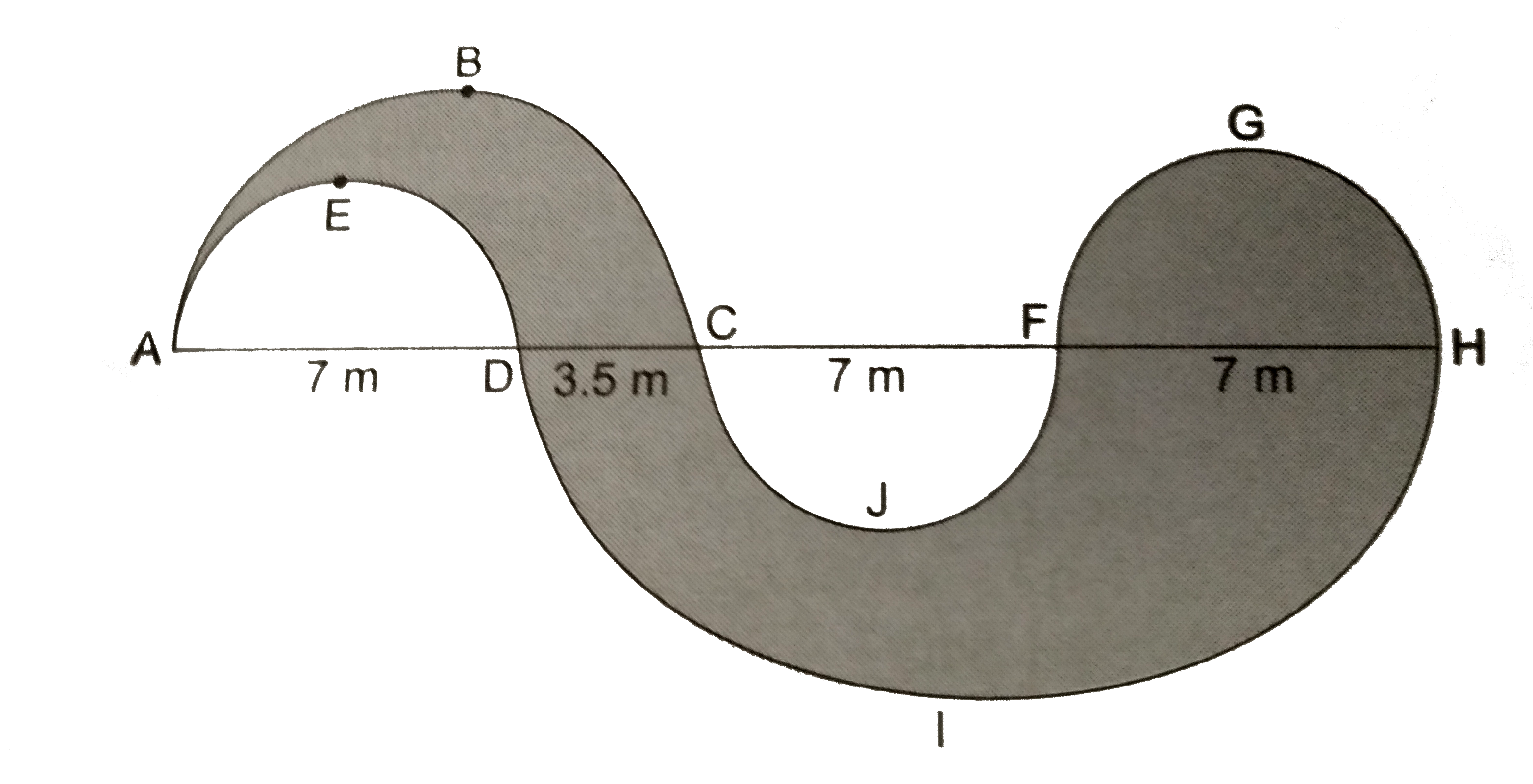
Area of the shaded region
=ar(ABCDEA)+ar(FGHF)+ar(HIDCJFH)
=ar(semicircleABC)−ar(semicircleAED)+ar(semicircleFGH)+ar(semicircleHID)−ar(semicircleFJC)
=[{12π×214×214}−{12π×72×72}+{12π×72×72}
+{12π×354×354}−{12π×72×72}]m2
={(227×44132)+(12×227×354×354)−(227×498)}m2
={(11×6316)+(55×3516)−774}m2=(69316+192516−774)m2
=(693+1925−30816)m2=11558m2=144.38m2.
Hence the required area is 144.38m2
Example 10
In the given figure ΔABC is a right angled triangle with ∠B=90∘,AB=48cm and BC=14cm. With AC as diameter a semicircle is drawn and with BC as radius, a quadrant of a circle is drawn. Find the area of the shaded region.
[Use π=227]
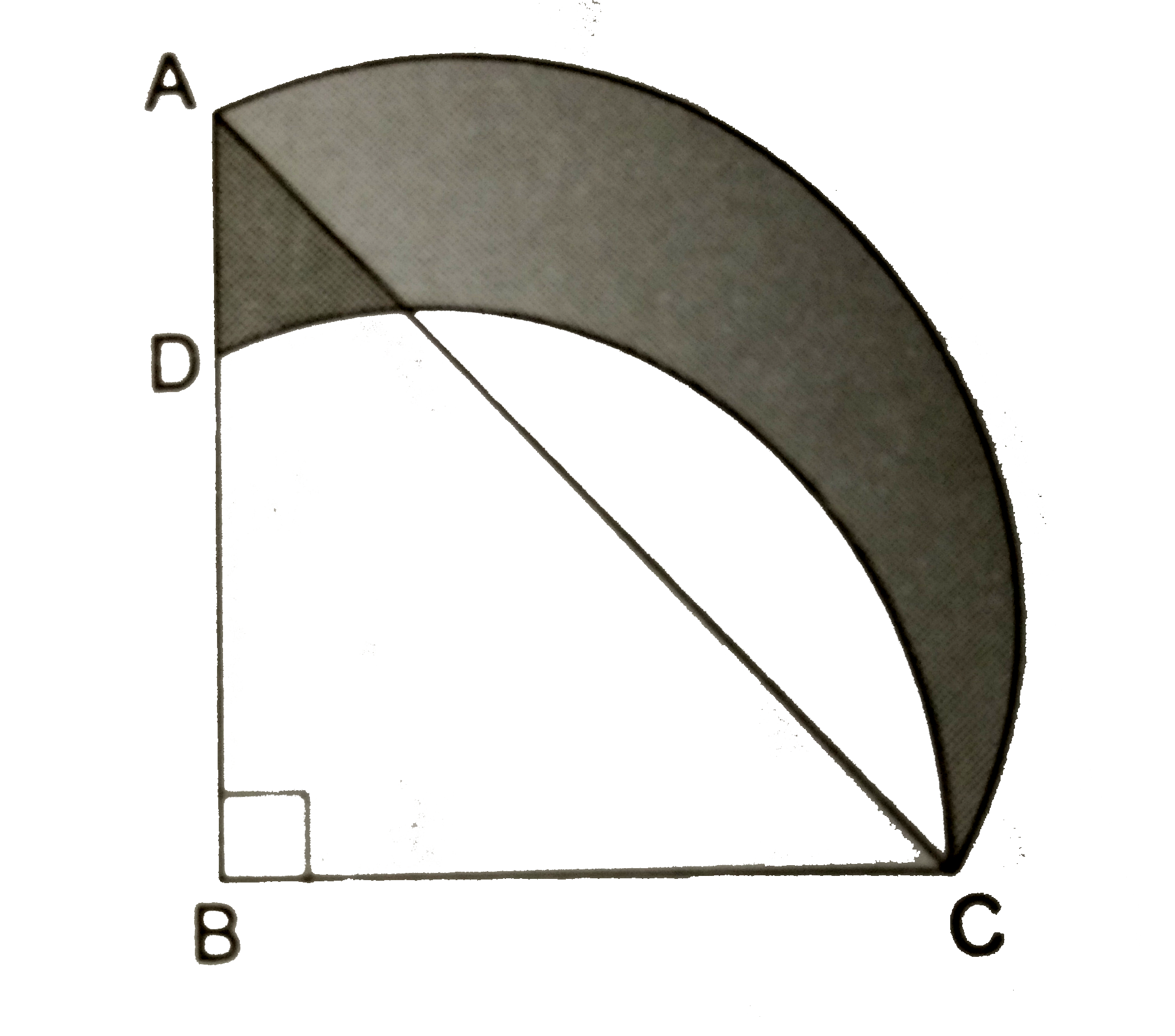
In right ΔABC, we have
AC2=AB2+BC2=(48)2+(14)2=(2304+196)=2500
⇒AC=√2500=50cm
⇒R=502cm=25cm
Area of the shaded region
=ar(ΔABC)+(area of semicircle onAC)−ar(quadrantBCD)
=(12×14×48)+12π×25×25−14π×BC2
[336+12×227×625−14×227×14×14]cm2
=(336+68757−154)cm2=(182−982−14)cm2
=1164.14cm2
Hence the area of the shaded region is 1164.14cm2
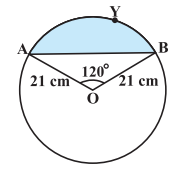
Example 11
Find the area of the segment AYB, if the radius of the circle is 21cm and ∠AOB=120°.(use π=227)
Area of the segment AYB
= Area of sector OAYB– Area of ΔOAB ...........(1)
Now, area of the sector OAYB=120360×227×(21)×(21)cm2=462cm2 ..........(2)
For finding the area of ΔOAB, draw OM⊥AB as shown in Figure below.
Note that OA=OB. Therefore, by RHS congruence, ΔAMO≅ΔBMO
So, M is the mid-point of AB and ∠AOM=∠BOM=(12)×120∘=60°
Let OM=xcm
So, from ΔOMA,OMOA=cos60°
or x21=12(cos60°=12)
x=212
So OM=212cm
Also AMOA=sin60°=√32
AM=21√32cm
Therefore, AB=2AM=(2×21√32cm)
=21√3cm
So, area of ΔOAB=(12)×(AB)×(OM)=(12)×(21√3)×(212)cm2
=441√34cm2 .........(3)
Therefore, area of the segment AYB=((462)−(441√34))cm2 [From (1), (2) and (3)]
=(214)(88–21√3)cm2.
CASE STUDY BASED QUESTION
A barn is an agricultural building usually on farms and used for various purposes. In the North American area, a barn refers to structures that house livestock, including cattle and horses, as well as equipment and fodder, and often grain.
Ramkaran want to build a barn at his farm. He has make a design for it which is above. Here roof is arc of a circle of radius r at centre O.
On the basis of the above information, answer any four of the following questions:
(i) What is the value of radius of arc ?
(a) 4√3m
(b) 4√2m
(c) 2√3m
(d) 2√2m
(ii) What is the length of BF ?
(a) 4(√3+1)
(b) 4(√2+1)
(c) 4(√3−1)
(d) 4(√2−1)
(iii) What is the value of angle ∠AOC ?
(a) 30∘
(b) 90∘
(c) 45∘
(d) 60∘
(iv) What is the curved width of roof ?
(a) 2π√3 m
(b) 4π√2 m
(c) 2π√2 m
(d) 4π√3 m
(v) What is area of cross section of barn ?
(a) 8(6+π) m2
(b) 4(6+π) m2
(c) 8(3+π) m2
(d) 4(3+π) m2
(i) We redraw the cross section of barn as shown below.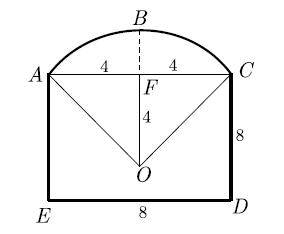
In right triangle △AFO
AO=√AF2+FO2
= 42+42=42m
Thus AO=4√2 which is also radius of curved arc.
(ii) BF=BO−FO=r−4=4(√2−4)=4(√2−1) m
(iii) In right angle triangle △AFO is also isosceles triangle
Thus, ∠FAO=∠FOA=45∘
Similarly, ∠FOC=45∘
Thus ∠AOC=∠AOF+∠FOC=45∘+45∘=90∘
(iv) Curved width
2πrθ360∘ = 2π×4√2×90∘360∘ = 2π√2 m
(v) Area of cross section
= Area of AECD + Area of section ABCO - Area of triangle ACO
= 8×8+π(4√2)2×90∘360∘−12×4×8
= 64+8π−16
= 48+8π
= 8(6+π)
Summary
1. Circumference of a circle = 2πr.
2. Area of a circle = πr2.
3. Length of an arc of a sector of a circle with radius r and angle with degree measure θ is θ360∘×2πr.
4. Area of a sector of a circle with radius r and angle with degree measure θ is θ360∘×πr2.
5. Area of segment of a circle = Area of the corresponding sector – Area of the corresponding triangle.
Let's Revise
To bachcho ab hum Areas Related to Circles chapter ka revision karenge.
- Area of circle =πr2 aur Circumference of circle =2πr (circumference ka matlab hota hai length of boundary of circle).
- Sector of Circle :
- Segment of Circle :
- Length of an arc of a sector(L) :
yha θ sector ka angle hai aur r, radius of circle hai.
- Area of a Sector of a Circle =
yha ∠θ sector ka angle hai aur r, radius of circle hai.
Note : Upar humney sirf minor sector ke barey mein discuss kiya hai.
- Area of triangle =
Area of equilateral triangle = (√34)×(side)2
- Area of Segment of a Circle = Area of sector in which it lies - Area of triangle formed by chord/secant with the two radii
=[(θ360°)×πr2]–[r2×sin(θ2)×cos(θ2)] if θ is known.
Yha θ sector ka angle hai aur r radius of circle hai.
- Area of Trapezium =