Complete Solutions to All Questions of chapter TRIANGLE AND ITS ANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLE AND ITS ANGLES |
| Mathematics | All Questions |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
In a Triangle ` A B C ,\ /_B=105^0,\ /_C=50^0,` Find `/_A`
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionOf the three angles of a triangle, one is twice the smallest and another is three times the smallest. Find the angles.
View SolutionIf the angle of a triangle are in the ratio `2:3:4,` determine three angles.
View SolutionThe sum of two angles of a triangle is `80^0` and their difference is `20^0dot` Find all the angles.
View SolutionIn a ` △ A B C ,` if `2/_A=3/_B=6\ /_C ,` determine `/_A ,\ /_B\ a n d\ /_C`
View Solution`A , B , C` are the three angles of a triangle. If `A-B=15^@,\ B-C=30^@,` find `/_A ,\ /_B\ a n d\ /_C`
View SolutionIn Figure AB||DC , if `x=(4y)/3` and `y=(3z)/8,` find `/_B C D ,/_A B C` and `/_B A Ddot`
View SolutionA triangle `A B C` is right angles at `AdotA L` is drawn perpendicular to `B C` . Prove that `/_B A L=\ /_A C B`
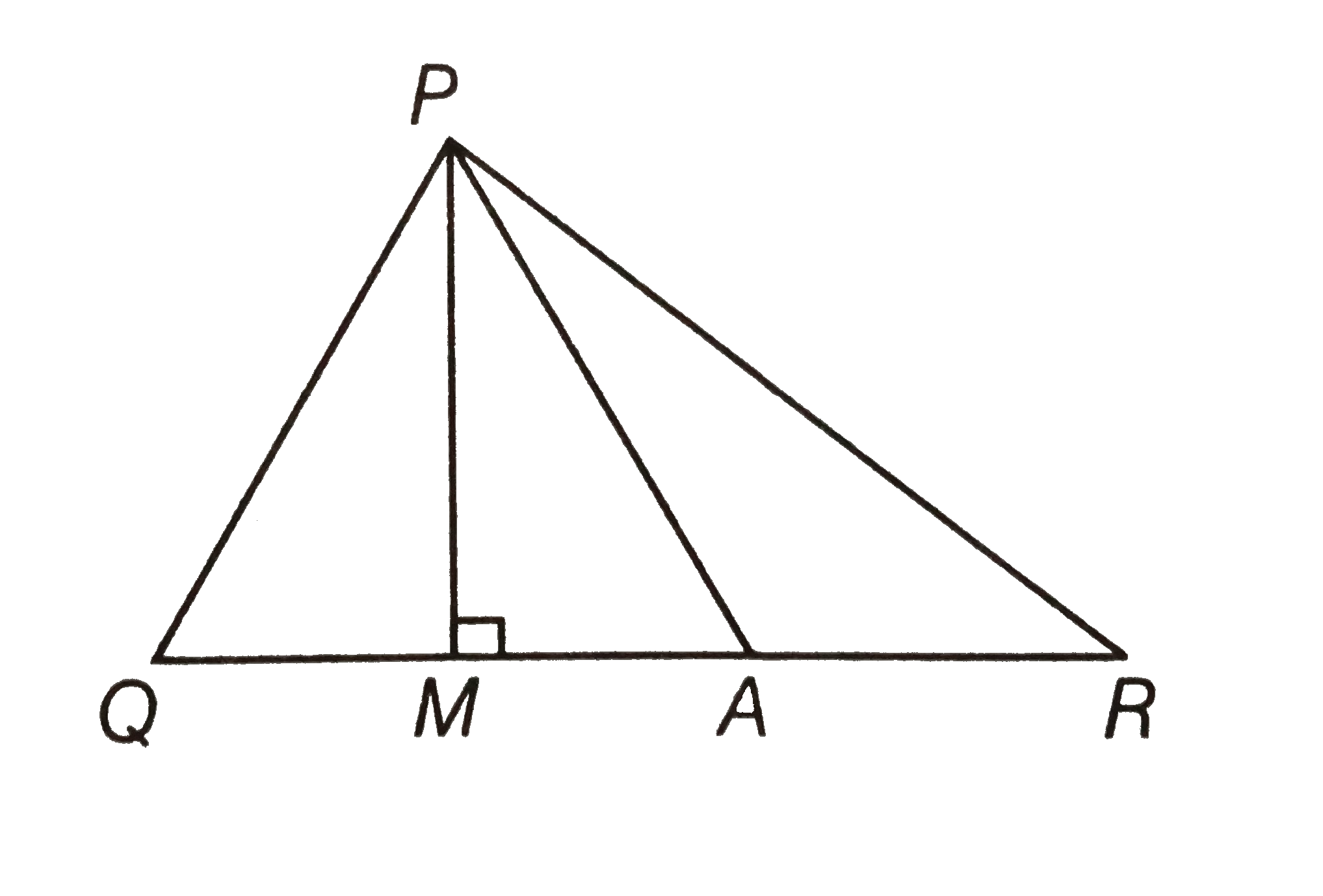
View SolutionIn the given figure , `/_`Qgt`/_`R, PA is the bisector of `/_`QPR and PM`bot` QR.
Prove that `/_`APM = 1/2(`/_`Q-`/_`R).
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIn Figure, `T Q\ a n d\ T R` are the bisectors of `/_Q\ a n d\ /_R` respectively. If `/_Q P R=80^0a n d\ /_P R T=30^0,` determine `/_T Q R\ a n d\ /_Q T R`
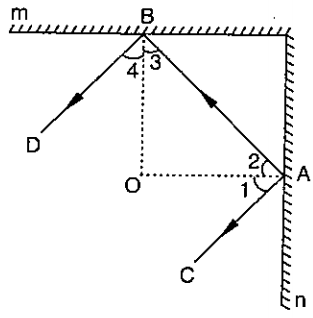
View SolutionIn Figure, `m\ and\ n` are two plane mirrors perpendicular to each other. Show that the incident ray `C A` is parallel to the reflected ray `B D`
View SolutionIn `△ A B C ,\ /_B=45^0,\ /_C=55^0` and bisector of `/_A` meets `B C` at a point `Ddot` Find `/_A D B\ a n d\ \ /_A D C`
View SolutionIn Figure, prove that PM=PN= root 3 × a
View SolutionIn a Triangle` A B C ,` if `/_A=55^0,\ /_B=40^0,` find `/_C`
View SolutionIf the angles of a triangle are in the ratio `1:2:3,` determine three angles.
View SolutionThe angles of a triangle are `(x-40)^0,\ (x-20)^0\ a n d\ (1/2x-10)^0dot` find the value of `xdot`
View SolutionThe angle of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is `10^0,` find the three angles.
View SolutionTwo angles of a triangle are equal and the third angle is greater than each of those angles by `30^0dot` Determine all the angles of the triangle.
View SolutionIf one angle of a triangle is equal to the sum of the other two, show that the triangle is a right triangle.
View Solution`A B C` is a triangle in which `/_A=72^0,` the internal bisectors of angles `B\ a n d\ C` meet in `Odot` Find the magnitude of `/_B O C`
View SolutionThe bisectors of base angles of a triangle cannot enclose a right angle in any case.
View SolutionIf the bisectors of the base angles of a triangle enclose an angle of `135^0,` prove that the triangle is a right triangle.
View SolutionIn a triangle ` A B C ,\ /_A B C=\ /_A C B` and the bisectors of `/_A B C\ a n d\ /_A C B` intersect at `O` such that `/_B O C=120^0dot` Show that `/_A=/_B=/_C=60^0` .
View SolutionCan a triangle have: Two right angles? (ii) Two obtuse angles? Two acute angles (iv) All angles more than `60^0` ? All angles less than `60^0` ? (vi) All angles equal to `60^0`
View SolutionIf each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
View SolutionAn exterior angle of a triangle is `11 0^0,` and one of the interior opposite angles is `30^0dot` Find the other two angles of the triangle.
View SolutionThe sides `B C ,\ C A\ a n d\ A B\ ` of a triangle ` A B C ,` are produced in order, forming exterior angles `/_A C D ,\ /_B A E\ a n d\ /_C B Fdot` Show that `/_A C D+\ /_B A E+\ /_C B F=360^0`
View SolutionIn Figure, if `Q T_|_P R ,\ /_T Q R=40^@\ a n d\ \ /_S P R=30^@,` find `x\ a n d\ y`.
View SolutionIn Figure, side `Q P\ a n d\ R Q` of ` P Q R` are produced to point `S\ a n d\ T` respectively. If `/_S P R=135^0a n d\ /_P Q T=110^@`, find `/_P R Q`
View SolutionIn Figure, `/_X=62^@,\ /_X Y Z=54^@`. If `Y O\ a n d\ Z O` are bisectors of `/_X Y Z\ a n d\ /_X Z Y` respectively of ` X Y Z ,` find `/_O Z Y\ a n d\ /_Y O Z`.
View SolutionIn Figure, if `A B\ || D E ,\ /_B A C=35^0a n d\ /_C D E=53^0,` find `/_D C Edot`
View SolutionIn Figure, if lines `P Q\ a n d\ R S` intersect at a point `T` such that `/_P R T=40^@,\ /_R P T=95^@a n d\ /_T S Q=75^@,` find `/_S Q T`.
View SolutionIn Figure, if `P Q_|_P S ,\ P Q S R ,\ /_S Q R=28^0a n d\ /_Q R T=65^0,` then find the values of `x\ a n d\ y`
View SolutionThe side `B C` of a ` A B C` is produced on both sides. Show that the sum of the exterior angles so formed is greater than `/_A` by two right angles.
View SolutionSides `B C ,\ C A\ a n d\ B A` of a triangle `A B C` are produced to `D ,\ Q ,\ P` respectively as shown in Figure. If `/_A C D=100^0a n d\ /_Q A P=35^0,` find all the angles of the triangle.
View SolutionIn Figure, the side `B C\ ` of ` /_\A B C` is produced to form ray `B D` as shown. Ray `C E` is drawn parallel to `B A` . Show directly, without using the angle sum property of a triangle that `A C D=\ /_A+/_B` and deduced that `/_A+/_B+/_C=180^@`.
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one-half of the vertical angle.
View SolutionThe side `B C\ ` of a ` A B C` is produced, such that `D` is one ray `B Cdot` The bisector of `/_A` meets `B C` in `L` as shown in Figure. Prove that `/_A B C+/_A C D=2/_A L C`
View SolutionThe exterior angles, obtained on producing the base of a triangle both ways are `104^0a n d\ 136^0dot` Find all the angles of the triangle.
View SolutionIn a triangle ` A B C ,` the internal bisectors of `/_B\ a n d\ /_C` meet at `P` and the external bisectors of `/_B\ a n d\ /_C` meet at `Q` . Prove that `/_B P C+\ /_B Q C=180^0`
View SolutionIn Figure, the sides `B C ,\ C A\ a n d\ A B` of a ` A B C` have been produced to `D ,\ E\ a n d\ F` respectively. If `/_A C D=105^0\ a n d\ \ /_E A F=45^0,` find all the angles of the `\ A B C`
View SolutionCompute the value of `x` in each of the following figures:
View SolutionIn Figure, `A B` divides `/_D A C` in the ratio `1\ :3\ a n d\ A B=D B`. Determine the value of `x`.
View Solution`A B C` is a triangle. The bisector of the exterior angle at `B` and the bisector of `/_C` intersect each other at `D`. Prove that `/_D=1/2/_A`.
View SolutionIn Figure, `A M\ _|_B C\ \ a n d\ A N` is the bisector of `/_Adot` If `/_B=65^0a n d\ /_C=33^0,` find `/_M A N`
View SolutionIn a `\ A B C ,\ A D` bisects `/_A\ a n d\ /_C >/_Bdot` Prove that `/_A D B >\ /_A D C` .
View SolutionIn Figure, `A E` bisects `/_C A D\ a n d\ /_B=/_Cdot` Prove that `A E||B C`
View SolutionIn Figure, `A B||D Edot` Find `/_A C D`
View SolutionWhich of the following statements are true (T) and which are false (F): Sum of the three angles of a triangle is `180^0` A triangle can have two right angles. All the angles of a triangle can be less than `60^0` All the angles of a triangle can be greater than `60^0` All the angles of a triangle can be equal to `60^0` A triangle can have two obtuse angles. A triangle can have at most one obtuse angles. In one angle of a triangle is obtuse, then it cannot be a right angled triangle. An exterior angle of a triangle is less than either of its interior opposite angles. An exterior angle of a triangle is equal to the sum of the two interior opposite angles. An exterior angle of a triangle is greater than the opposite interior angles
View SolutionFill in the blanks to make the following statements true: Sum of the angles of a triangle is ............ An exterior angle of a triangle is equal to the two ............ opposite angles. An exterior angle of a triangle is always ............ than either of the interior opposite angles. A triangle cannot have more than ............ right angles. A triangles cannot have more than ............ obtuse angles.
View SolutionDefine a triangle.
View SolutionWrite the sum of the angles of an obtuse triangle.
View SolutionIn ` A B C ,` if `/_B=60^0,\ /_C=80^0` and the bisectors of angles `/_A B C\ a n d\ /_A C B` meet at a point `O ,` then find the measure of `/_B O C.`
View SolutionIf the angle of a triangle are in the ratio `2:1:3,` then find the measure of smallest angle.
View SolutionIf the angles `A ,\ B\ a n d\ C` of a `/_\ A B C` satisfy the relation `B-A=C-B ,` then find the measure of `/_B`.
View SolutionIn ` A B C ,` if bisectors of `/_A B C\ a n d\ /_A C B` intersect at `O` at angle of `120^0` , then find the measure of `/_A`
View SolutionState exterior angle theorem
View SolutionIf the side `B C` of ` A B C` is produced on both sides, then write the difference between the sum of the exterior angles so formed and `/_A`.
View SolutionIn a triangle `A B C ,` if `A B=A C\ a n d\ A B` is produced to `D` such that `B D=B C ,` find `/_A C D\ :\ /_A D C`
View SolutionThe sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
View SolutionIn Figure, if `A B || C D ,\ E F || B C ,\ /_B A C=65^@` and `/_D H F=35^@,` find `/_A G H`.
View SolutionIn Figure, if `A B || D F` and `B D || F G` such that `/_F G H=120^@` and `/_B=50^@,` find `x\ a n d\ y`.
View SolutionIn Figure, side `B C\ ` of ` A B C` is produced to point `D` such that bisectors of `/_A B C\ a n d\ /_A C D` meet at a point `Edot` If `/_B A C=68^0,` find `/_B E C`
View SolutionIf all the three angles of a triangle are equal, then each one of them is equal to: (a)`90^0` (b) `45^0` (c) `60^0` (d) `30^0`
View SolutionIf two acute angles of a right triangle are equal, then each acute is equal to (a)`30^0` (b) `45^0` (c) `60^0` (d) `90^0`
View SolutionAn exterior angle of a triangle is equal to `100^0` and two interior opposite angles are equal. Each of these angles is equal to (a)`75^0` (b) `80^0` (c) `40^0` (d) `50^0`
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View SolutionSide `B C` of a triangle `A B C` has been produced to a point `D` such that `∠ACD = 120^0dot` If `/_B=1/2/_A ,` then `/_A` is equal to `80^0` (b) `75^0` (c) `60^0` (d) `90^0`
View SolutionIn ` A B C ,\ /_B=/_C` and ray `A X` bisects the exterior angle `/_D A CdotIf\ /_D A X=70^0,\ t h e n\ /_A C B=` (a)`35^0` (b) `90^0` (c) `70^0` (d) `55^0`
View SolutionIn a triangle, an exterior angle at a vertex is `95^0` and its one of the interior opposite angle is `55^0` , then the measure of the other interior angle is (a) `55^0` (b) `85^0` (c) `40^0` (d) `90^0`
View SolutionIf the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is (a)`90^0\ ` (b) `180^0` (c) `270^0` (d) `360^0`
View SolutionIn △ A B C ,` if ``/_A=100^0,\ A D` bisects `/_A\ a n d\ /_A D\ _|_B C` . Then, `∠ACD`` (a) ``50^0` (b) `90^0` (c) `40^0` (d) `100^0``
View SolutionAn exterior angle of a triangle is `108^0` and its interior opposite angles are in the ratio 4:5. The angles of the triangle are (a)`48^0,\ 60^0,\ 72^0` (b) `50^0,\ 60^0,\ 70^0` (c)`52^0,\ 56^0,\ 72^0` (d) `42^0,\ 60^0,\ 76^0`
View SolutionIn a ` A B C ,` if `/_A=60^0,\ /_B=80^0` and the bisectors of `/_B\ a n d\ /_C` meet at `O ,` then `/_B O C=` (a)`60^0` (b) `120^0` (c) `150^0` (d) `30^0`
View SolutionIf the bisectors of the acute angles of a right triangle meet at `O ,` then the angle at `O` between the two bisectors is (a)`45^0` (b) `95^0` (c) `135^0` (d) `90^0`
View SolutionLine segments `A B\ a n d\ C D` intersect at `O` such that `A C = D Bdot` If `/_C A B=45^0a n d\ /_C D B=55^0,` then `/_B O D=` (a)`100^0` (b) `80^0` (c) `90^0` (d) `135^0`
View SolutionThe bisects of exterior angles at B and C of triangle `A B C` meet at `O`. If `A=x^@,` then `B O C=`
(a)`90^0+(x^0)/2`
(b) `90^0-(x^0)/2`
(c)`180^0+(x^0)/2`
(d) `180^0-(x^0)/2`
View SolutionIn a ` A B C ,\ /_A=50^0a n d\ B C` is produced to a point `Ddot` If the bisectors of `/_A B C\ a n d\ /_A C D` meet at `E ,` then `/_E=` (a)`25^0` (b) `50^0` (c) `100^0` (d) `75^0`
View SolutionThe side `B C` of ` A B C` is produced to a point `Ddot` The bisector of `/_A` meets side `B C` in `Ldot` If `/_A B C=30^0a n d\ /_A C D=115^0,` then `/_A L C=` `85^0` (b) `72 1/2^0` (c) `145^0` (d) none of these
View SolutionIn Figure, if `E C || A B ,\ /_E C D=70^0A N D\ /_B D O=20^0` , then `/_O B D` is: `20^0` (b) `50^0` (c) `60^0` (d) `70^0`
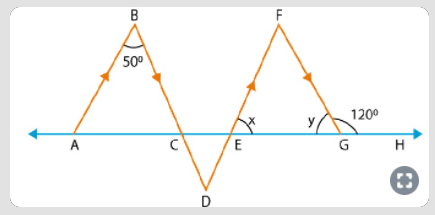
View SolutionIn Figure, `x+y=` 270 (b) 230 (c) 210 (d) `190^0`
View SolutionIf the measures of angles of a triangle are in the ratio of `3:4:5,` what is the measure of the smallest angle of the triangle? (a)`25^0` (b) `30^0` (c) `45^0` (d) `60^0`
View SolutionIn Figure, if `A B_|_B C ,` then `x=` 18 (b) 22 (c) 25 (d) 32
View SolutionIn Figure, what is `z` in terms of `\ a n d\ y` ? `x+y+180` (b) `x+y-180` `180^0-(x+y)` (d) `x+y+360^0`
View SolutionIn Figure, for which value of `x` is `l_1 l_2` ? 37 (b) 43 (c) 45 (d) 47
View SolutionIn Figure, what is `y` in terms of `x\ ?` (a)`3/2x` (b) `4/3x` (c) `x` (d) `3/4x`
View SolutionIn Figure, if `l_1 || l_2,` the value of `x` is
(a) `22 1/2`
(b) `30`
(c) 45
(d) 60
View SolutionIn Figure, what is the value of `x ?` (a)35 (b) 45 (c) 50 (d) 60
View SolutionIn triangle ` R S T ,\ ` what is the value of `x\ ?` (a)`40^0` (b) `90^0` (c) `80^0` (d) `100^0`
View SolutionIn Figure, the value of `x` is `65^0` (b) `80^0` (c) `95^0` (d) `120^0`
View SolutionIn Figure, if `B P||C Q` and `A C=B C` , then the measure of `x` is (a)`20^0` (b) `25^0` (c) `30^0` (d) `35^0`
View SolutionIn Figure, `A B\ a n d\ C D` are parallel lines and transversal `E F` intersects them at `P\ a n d\ Q` respectively. If `/_A P R=25^0,\ /_R Q C=30^0a n d\ /_C Q F=65^0,` then
(a) `x=55^0,\ y=40^0`
(b) `x=50^0,\ y=45^0`
(c) `x=60^0,\ y=35^0`
(d) `x=35^0,\ y=60^0`
View SolutionThe base `B C` of triangle `A B C` is produced both ways and the measure of exterior angles formed are `94^0a n d\ 126^0dot` Then `/_B A C (a) ` `94^0` (b) `54^0` (c) `40^0` (d) `44^0`
View Solution
All Questions questions and complete solutions for chapter TRIANGLE AND ITS ANGLES of RD SHARMA MATHS (ENGLISH) of Class 9