Compute the value of in each of the following figures:
To compute the value of x in the given figures, let's break down the solution step by step for each figure.
Figure 1:
1. Identify the Angles: In the first figure, we have two angles, angle AOC and angle AOB. We know that these angles form a linear pair.
2. Set Up the Equation: Since angle AOC and angle AOB form a linear pair, their sum is equal to 180 degrees. Therefore, we can write the equation:
Angle AOC+Angle AOB=180∘
Given that angle AOC = 75 degrees and angle AOB = 5x + 20 degrees, we can substitute these values into the equation:
75+(5x+20)=180
3. Simplify the Equation: Combine like terms:
75+5x+20=180
This simplifies to:
5x+95=180
4. Isolate x: Subtract 95 from both sides:
5x=180−95
5x=85
5. Solve for x: Divide both sides by 5:
x=855=17
Conclusion for Figure 1:
The value of x is 17 degrees.
---
Figure 2:
1. Identify the Angles: In the second figure, we have several angles: 65 degrees, 75 degrees, x, and 2x, and 3x. We need to find the value of x.
2. Set Up the Equation: The sum of angles around a point is 360 degrees. Therefore, we can write the equation:
65+2x+75+x+3x=360
3. Combine Like Terms: Combine the constant terms and the terms with x:
(65+75)+(2x+x+3x)=360
This simplifies to:
140+6x=360
4. Isolate x: Subtract 140 from both sides:
6x=360−140
6x=220
5. Solve for x: Divide both sides by 6:
x=2206≈36.67
Conclusion for Figure 2:
The value of x is approximately 36.67 degrees.
---
2. Set Up the Equation: Since angle AOC and angle AOB form a linear pair, their sum is equal to 180 degrees. Therefore, we can write the equation:
Angle AOC+Angle AOB=180∘
Given that angle AOC = 75 degrees and angle AOB = 5x + 20 degrees, we can substitute these values into the equation:
75+(5x+20)=180
75+5x+20=180
This simplifies to:
5x+95=180
5x=180−95
5x=85
x=855=17
The value of x is 17 degrees.
65+2x+75+x+3x=360
(65+75)+(2x+x+3x)=360
This simplifies to:
140+6x=360
6x=360−140
6x=220
x=2206≈36.67
The value of x is approximately 36.67 degrees.
Topper's Solved these Questions
Similar Questions
Find the value of x in each of the following figures.
View SolutionFind the value of x in each of the following figures.
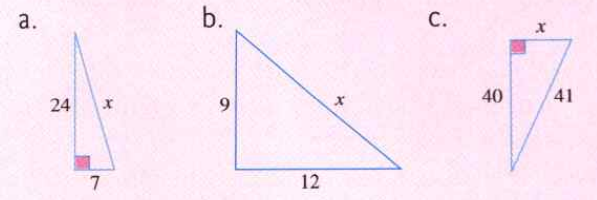
View SolutionCalculate the value of x in each of the following figures :
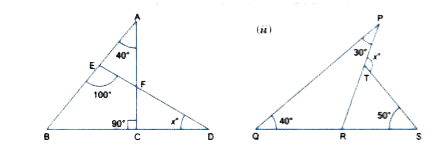
View SolutionCalculate the value of x in each of the following figures :
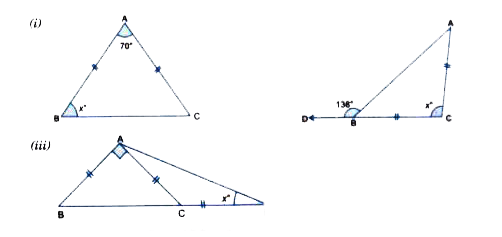
View SolutionCalculate the value of x in each of the following figures :
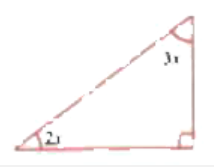
View SolutionCalculate the value of x in each of the following figures :
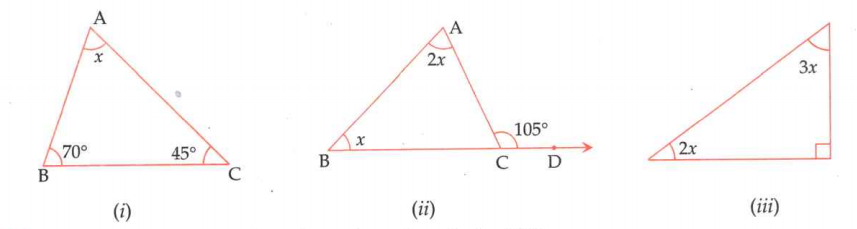
View SolutionIf O is the center of the circle, find the value of x in each of the following figures:
View SolutionCalculate the value of x in each of the following figures and name the triangle (on the basis of angles):
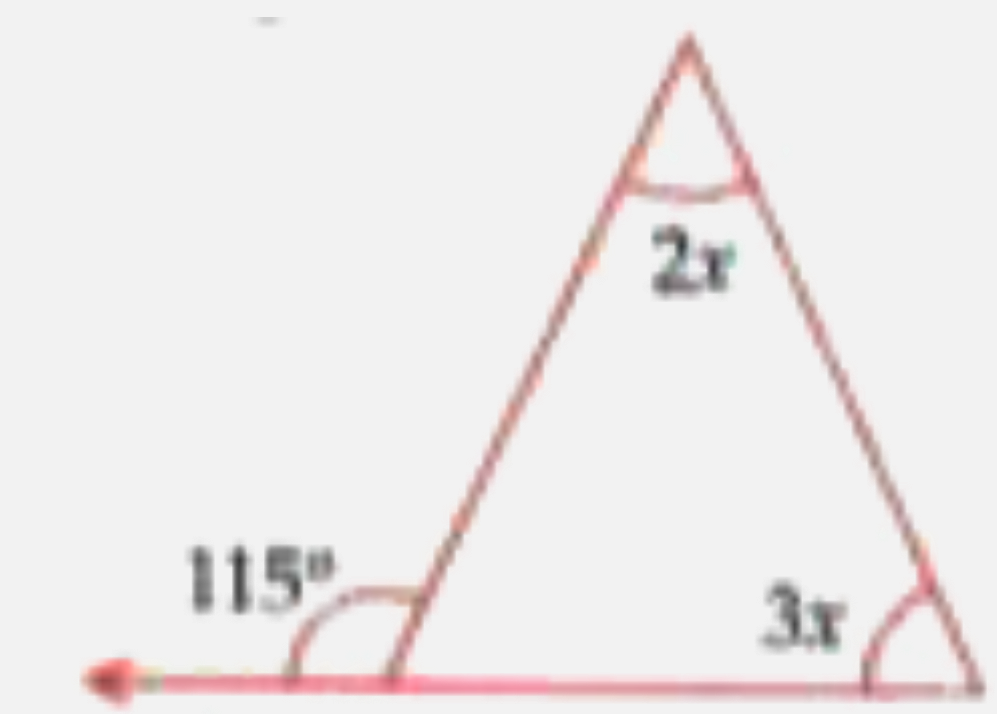
View SolutionCalculate the value of x in each of the following figures and name the triangle (on the basis of angles):

View SolutionCalculate the value of x in each of the following figures and name the triangle (on the basis of angles):
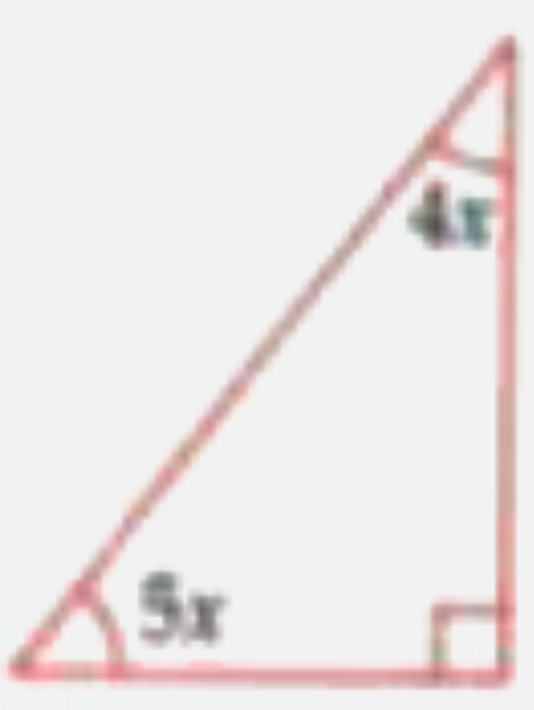
View Solution

