Complete Solutions to LONG ANSWER QUESTIONS - I of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| U-LIKE SERIES | LONG ANSWER QUESTIONS - I |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
The electron drift speed is estimated to be only a few mm `s^(-1)` for currents in the range of a few amperes. How then is current established almost the instant a circuit is closed ?
View SolutionThe electron drift arises due to the force experienced by electrons in the electric field inside the conductor. But force should cause acceleration. Why then do the electrons acquire a steady average drift speed ?
View SolutionIf the electron drift speed is so small and the electron's charge is small, how can we still obtain large amounts of current in a conductor ?
View SolutionWhen electrons drift in a metal from lower to higher potential, does it mean that all the 'free' electrons of the metal are moving in the same direction ?
View SolutionAre the paths of electrons straight lines between successive collisions (with the positive ions of the metal) in the (i) absence of electric field, (ii) presence of electric field ?
View SolutionDefine the terms (i) drift velocity, (ii) relaxation time. A conductor of length L is connected to a d.c. source of emf `epsi` . If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change ?
View SolutionDerive an expression for the resistivity of a good conductor in terms of the relaxation time of electrons.
View SolutionDefine relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.
View SolutionDefine the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity `(sigma)` of the conductor when an electric field E is applied to it.
View Solution(a) Deduce the relation between current I flowing through a conductor and drift velocity `vecv_d` of the electrons.
(b) Figure shows a plot of current I flowing through the cross section of a wire versus the time t. Use the plot to find the charge flowing in 10 s through the wire.
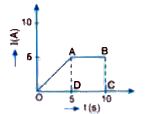
View Solution(a) Define the term conductivity of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
View SolutionA cell of emf `epsi` and internal resistance 'r' is connected across a variable load resistor 'R'. Draw the plots of the terminal voltage 'V' versus (i) R and (ii) the current I.
It is found that when R = 4 `Omega` , the current is 1 A and when R is increased to 9 `Omega` , the current reduces to 0.5 A. Find the values of the emf `epsi` and internal resistance r.
View SolutionA number of identical cells, n, each of emf `epsi` , internal resistance r connected in series are charged by a d.c. source of emf `epsi` , using a resistor R.
(i) Draw the circuit arrangement.
(ii) Deduce the expressions for (a) the charging current and (b) the potential difference across the combination of the cells.
View SolutionTwo cells of emf `epsi_1` and `epsi_2` having internal resistances `r_1` and `r_2` respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the points` B_1` and `B_2` .

View Solution(a) The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor us 9. By what factor docs the applied potential difference change?
(b) In the figure shown, an ammeter A and a resistor of 4`Omega` are connected to the terminals of the source. The emf of the source is 12 V having an internal resistance of 2`Omega` . Calculate the voltmeter and ammeter readings.
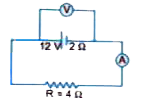
View SolutionThe temperature coefficient of resistivity for two materials A and B are `0.0031//""^@C` , and `0.0068//""^@C` respectively. Two resistors `R_1` and `R_2`, made from material A and B respectively, have resistances of 200 `Omega` and 100 `Omega` at `0^@C` . Show the colour code of a carbon resistor that would have a resistance equal to the series combination of `R_1` and `R_2` at a temperature of `100^@C` (Neglect the ring corresponding to the tolerance of the carbon resistor).
View SolutionIn the circuit shown , find the current through resistors.

View SolutionUse Kirchhoff's rules to obtain the balance condition in a Wheatstone bridge.
View SolutionWith the help of a circuit diagram, explain the working principle of metre bridge. How is it used to determine the unknown resistance of a given wire ? Write the necessary precautions to minimise error in the result.
View SolutionState the working principle of a potentiometer. With the help of the circuit diagram explain how a potentiometer is used to compare the emfs of two primary cells. Obtain the required expression used for comparing the emfs.
View SolutionWrite the principle of working of a potentiometer. Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a cell.
View SolutionA resistance of R`Omega` draws current from a potentiometer as shown in Fig. The potentiometer has a total resistance `R_0 Omega`. A voltage Vis supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.

View SolutionA student uses the circuit diagram of a potentiometer as shown in Fig.
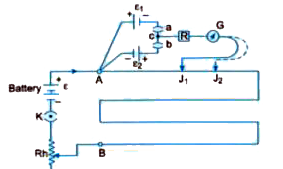
(a) For a steady current I passing through the potentiometer wire, he gets a null point for the cell `epsi_1`and not for `epsi_2` . Give reason for this observation and suggest how this difficulty can be resolved.
(b) What is the function of resistance R used in the circuit? How will the change in its value affect the null point ?
(c ) How can the sensitivity of the potentiometer be increased?
View Solution(i) State the principle of working of a metre bridge.
(ii) In a metre bridge balance point is found at a distance `l_1` with resistances R and S as shown in the figure.
When an unknown resistance X is connected in parallel with the resistance S, the balance point shifts to a distance l. Find the expression for X in terms of `l_1 ,l_2` and S.
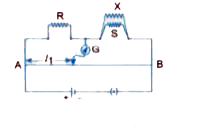
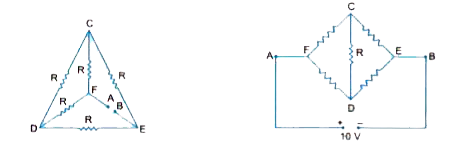
View Solution(i) Calculate the equivalent resistance of the given electrical network between points A and B.
(ii) Also calculate the current through CD and ACB, if a 10 V d.c. source is connected between A and B and the value of R is assumed as `2Omega`.
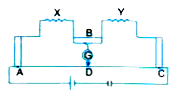
View SolutionThe Fig. shows experimental set up of a metre bridge. When the two unknown resistances X and Yare inserted, the null point Dis obtained 40 cm from the end A. When a resistance of 10`Omega` is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10`Omega` resistance is instead | А connected in series with resistance ‘Y. Determine the values of the resistances X and Y.
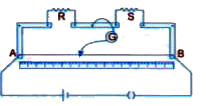
View SolutionIn a metre bridge the null point is found at a distance of 60.0 cm from A. If now a resistance of 5`Omega` is connected in series with S, the null point occurs at 50 cm. Determine the values of R and S.
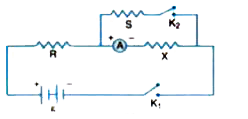
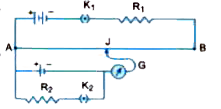
View SolutionThe reading of an ideal ammeter, in the circuit shown here, equals (i) I when key `K_1` is closed but key `K_2` is open , (ii) `I/2` when both keys `K_1` and `K_2` are closed. Find the expression for the resistance of X in terms of the resistance R and S.
View SolutionFor the potentiometer circuit shown in the given figure, points X and Y represent the two terminals of an unknown emf `epsi` . A student observed that when the jockey is moved from the end A to the end B of the potentiometer wire, the direction of the deflection in the galvanometer remains in the same direction. What may be the two possible faults in the circuit that could result in this observations ? If the galvanometer deflection at the end B is (i) more, (ii) less, than that at the end A which of the two faults," listed above, would be there in the circuit ? Give reasons in support of your answer in each case.
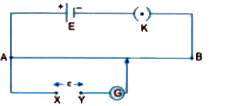
View Solution(a) For the circuit shown in the figure, how would the balancing length be affected, if (i) `R_1` is decreased, (ii) `R_2` is increased, the other factors remaining the same in the circuit ? Justify your answer in each case.
(b) Why is a potentiometer preferred over a voltmeter ? Give reason.
View SolutionTwo cells of emf 1.5 V and 2 V and internal resistance 1`Omega` and 2`Omega` respectively are connected in parallel to pass a current in the same direction through an external resistance of 5`Omega`.
(i) Draw the circuit diagram.
(ii) Using Kirchhoff's laws, calculate the current through each branch of the circuit and potential difference across the 5`Omega` resistor.
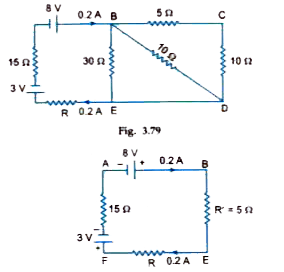
View SolutionCalculate the value of the resistance R in the circuit shown in Fig. so that the current in the circuit is 0.2 A. What would be the potential difference between points B and E ?
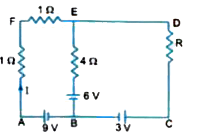
View SolutionUsing Kirchhoff's rules determine the value of unknown resistance R in the circuit so that no current flows through 4 `Omega` resistance. Also find the potential difference between A and D.
View SolutionState Kirchhoff's rules of current distribution in an electrical network. Using these rules determine the value of the current `I_1` in the electric circuit of Fig.
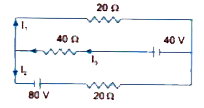
View SolutionState Kirchhoff's rules. Use these rules to write the expressions for the currents `I_1,I_2` and `I_3` in the circuit diagram shown in Fig.
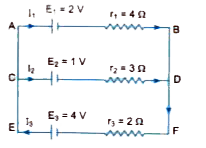
View SolutionState Kirchhoff's rules. Apply these rules to the loops PRSP and PRQP to write the expressions for the currents `I_1, I_2` and `I_3` in the given circuit of Fig.
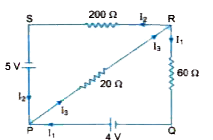
View SolutionIn the circuit shown , `R_1=4Omega, R_2=R_3 =15Omega, R_4 = 30 Omega ` and `epsi = 10V` . Calculate the equivalent resistance of the circuit and the current in each resistor.
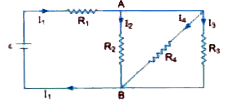
View SolutionTwo cells of same emf `epsi` but internal resistances `r_1` and `r_2` are connected in series to an external resistor R. What should be the value of R so that the potential difference across the terminals of the first cell becomes zero.

View SolutionIn the electric network shown in the Fig., use Kirchhoff's rules to calculate the power consumed by the resistance `R = 4 Omega`
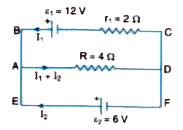
View SolutionUsing Kirchhoff's rules, calculate the potential difference between B and D in the circuit diagram as shown in Fig.
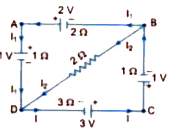
View SolutionTwo heating elements of resistances `R_1` and `R_2` when operated at a constant supply of voltage, V, consume powers `P_1` and `P_2` respectively. Deduce the expressions for the power of their combination when they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.
View SolutionA potentiometer wire of length 1 m is connected to a driver cell of emf 3 V as shown in the Fig. When a cell of 1.5 V emf is used in the secondary circuit, the balance point is found to be 60 cm. On replacing this cell and using a cell of unknown emf, the balance point shifts to 80 cm.
(i) Calculate unknown emf of the cell.
(ii) Explain with reason, whether the circuit works, if the driver cell is replaced with a cell of emf 1V.
(iii) Does the high resistance R, used in the secondary circuit affect the balance point? Justify your answer.
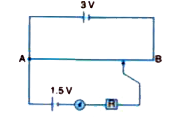
View SolutionA 10 m long wire of uniform cross-section and 20`Omega` resistance is used in a potentiometer. The wire is connected in series with a battery of 5 V along with an external resistance of 480 2. If an unknown emf E is balanced at 6.0 m length of the wire, calculate (i) the potential gradient of the potentiometer wire, (ii) the value of unknown emf.
View SolutionA circuit using a potentiometer and battery of negligible internal resistance is set up as shown in Fig. to develop a constant potential gradient along the wire AB. Two cells of emfs `epsi_1` and `epsi_2` are connected in series as shown in combinations (1) and (2). The balance points are obtained respectively at 400 cm and 240 cm from the point A. Find (i) `epsi_1/epsi_2` , (ii) balancing length for the cell `epsi_1` only .
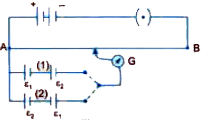
View SolutionIn the Fig., a long uniform potentiometer wire AB is having a constant potential gradient along its length. The null points for the two primary cells of emf `epsi_1` and ` epsi_2` connected in the manner shown are obtained at a distance of 120 cm and 300 cm from the end A. Find `(i) epsi_1//epsi_2 ` and (ii) position of null point for the cell `epsi_1`. How is the sensitivity of a potentiometer increased ?

View SolutionTwo conductors are made of the same material and have the same length. Conductor A is a solid wire of diameter 1 mm. Conductor B is a hollow tube of outer diameter 2 mm and inner diameter 1 mm. Find the ratio of resistances `R_A` to `R_B`
View SolutionA potentiometer wire of length 1 m has a resistance of 10 `Omega` . It is connected to a 6 V battery in series with a resistance of 5 `Omega` . Determine the emf of the primary cell which gives a balance point at 40 cm.
View Solution
LONG ANSWER QUESTIONS - I questions and complete solutions for chapter CURRENT ELECTRICITY of U-LIKE PHYSICS (HINGLISH) of Class 12
All Exercises from U-LIKE SERIES Class 12 PHYSICS CURRENT ELECTRICITY
- ADDITIONAL EXERCISES
- ASSERTION-REASON TYPE QUESTIONS
- CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
- FILL IN THE BLANKS
- LONG ANSWER QUESTIONS - I
- LONG ANSWER QUESTIONS - II
- MULTIPLE CHOICE QUESTIONS
- NCERT TEXTBOOK EXERCISES
- SELF ASSESSMENT TEST (SECTION A (FILL IN THE BLANKS))
- SELF ASSESSMENT TEST (SECTION A (MULTIPLE CHOICE QUESTIONS))
- SELF ASSESSMENT TEST (SECTION C )
- SHORT ANSWER QUESTIONS
- TRUE OR FALSE
- VERY SHORT ANSWER QUESTIONS