Complete Solutions to CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| U-LIKE SERIES | CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Answer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field `vecE` is applied across a piece of conductor, electrons will be accelerated at `veca = (e vecE)/(m)` . If `veca` was the velocity of electron after the last collision then velocity `vec v_t` after a time t will be `vecv_t = vecu + veca t`
The average velocity of the electrons at time t is the average of all`vec v'` s. However, average value of `vecu'`s is zero. As collisions of the electrons occur at random times, let `tau` be the average time between successive collision and then the average velocity electrons is expressed as `vecv_d` (known as the drift velocity) and is given as:
`vecv_d = - (e vecE)/(m) tau`
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : `I = nAev_d`, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of `10^(-3) ms^(-1)` for currents in the range of a few amperes.
Define drift velocity. On what factors does it depend ?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field `vecE` is applied across a piece of conductor, electrons will be accelerated at `veca = (e vecE)/(m)` . If `veca` was the velocity of electron after the last collision then velocity `vec v_t` after a time t will be `vecv_t = vecu + veca t`
The average velocity of the electrons at time t is the average of all`vec v'` s. However, average value of `vecu'`s is zero. As collisions of the electrons occur at random times, let `tau` be the average time between successive collision and then the average velocity electrons is expressed as `vecv_d` (known as the drift velocity) and is given as:
`vecv_d = - (e vecE)/(m) tau`
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : `I = nAev_d`, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of `10^(-3) ms^(-1)` for currents in the range of a few amperes.
If the electron drift speed is so small and the electron charge is small, how can we still obtain large amounts of current even in a thin conducting wire ?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field `vecE` is applied across a piece of conductor, electrons will be accelerated at `veca = (e vecE)/(m)` . If `veca` was the velocity of electron after the last collision then velocity `vec v_t` after a time t will be `vecv_t = vecu + veca t`
The average velocity of the electrons at time t is the average of all`vec v'` s. However, average value of `vecu'`s is zero. As collisions of the electrons occur at random times, let `tau` be the average time between successive collision and then the average velocity electrons is expressed as `vecv_d` (known as the drift velocity) and is given as:
`vecv_d = - (e vecE)/(m) tau`
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : `I = nAev_d`, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of `10^(-3) ms^(-1)` for currents in the range of a few amperes.
Are the paths of electrons straight lines between successive collisions in the (i) absence of electric field, (ii) presence of electric field ?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field `vecE` is applied across a piece of conductor, electrons will be accelerated at `veca = (e vecE)/(m)` . If `veca` was the velocity of electron after the last collision then velocity `vec v_t` after a time t will be `vecv_t = vecu + veca t`
The average velocity of the electrons at time t is the average of all`vec v'` s. However, average value of `vecu'`s is zero. As collisions of the electrons occur at random times, let `tau` be the average time between successive collision and then the average velocity electrons is expressed as `vecv_d` (known as the drift velocity) and is given as:
`vecv_d = - (e vecE)/(m) tau`
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : `I = nAev_d`, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of `10^(-3) ms^(-1)` for currents in the range of a few amperes.
Guess the order of magnitude of thermal speed of free electrons in a conductor in the absence of an external electric field.
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts :
Bulk matter is made up of many molecules, which are so closely packed that the electrons are no longer attached to individual nuclei. In metallic conductors some of the electrons are practically free to move within the bulk material. Ordinarily, the electrons will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random and there is no preferential direction for the velocities of the electrons. So number of electrons travelling in any direction will be equal to the number of electrons travelling in the opposite direction and there will be no net flow of electrons and hence no net current.
When an external electric field `vecE` is applied across a piece of conductor, electrons will be accelerated at `veca = (e vecE)/(m)` . If `veca` was the velocity of electron after the last collision then velocity `vec v_t` after a time t will be `vecv_t = vecu + veca t`
The average velocity of the electrons at time t is the average of all`vec v'` s. However, average value of `vecu'`s is zero. As collisions of the electrons occur at random times, let `tau` be the average time between successive collision and then the average velocity electrons is expressed as `vecv_d` (known as the drift velocity) and is given as:
`vecv_d = - (e vecE)/(m) tau`
This drift motion of electrons is responsible for establishment of an electric current in the conductor on applying an external electric field across it. The magnitude of current is given as : `I = nAev_d`, where n= number density of free electrons and A = cross-section area of the conductor. It is to be noted here that drift speed is estimated to be of the order of `10^(-3) ms^(-1)` for currents in the range of a few amperes.
What is the rate of flow of electric field through the conductor ?
View SolutionStudy the table given below:

The above table gives I-V relationship for a manganin coil prepared from a wire of cross-section area `1 xx 10^(-7)m^2` and length 4.1 m.
Now answer the following questions :
(a) Does the maganin coil behave as an ohmic resistor ?
(b) What is its electrical resistance ?
(c) Determine the resistivity of manganin.
(d) Compare the resistivity of manganin with that of copper.
(e) Why do you consider manganin an ideal choice for preparing standard resistors ?
View SolutionThe following table gives the lengths of four aluminium rods of uniform cross-section their diameters and potential difference maintained across the opposite ends of the rods. All the four rods are maintained at the same temperature.

Now answer the following questions :
(a) Which rod has maximum resistance ? (b) Which rod carries the maximum current ? (c) In which rod is the drift speed of electrons maximum ? (d) In which rod does the dissipation of electric energy take place at a maximum rate ? Give reason for each of your answer.
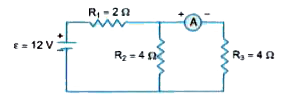
View SolutionAn ideal battery of emf 12 V is connected across an electric network shown here.

Now answer the following questions:
The equivalent resistance of the network is :
View SolutionAn ideal battery of emf 12 V is connected across an electric network shown here.
Now answer the following questions:
Net current drawn by the circuit from the battery is:
View SolutionAn ideal battery of emf 12 V is connected across an electric network shown here.
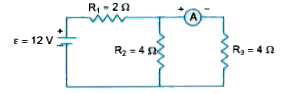
Now answer the following questions:
The reading of ammeter A is
View Solution
CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS questions and complete solutions for chapter CURRENT ELECTRICITY of U-LIKE PHYSICS (HINGLISH) of Class 12
All Exercises from U-LIKE SERIES Class 12 PHYSICS CURRENT ELECTRICITY
- ADDITIONAL EXERCISES
- ASSERTION-REASON TYPE QUESTIONS
- CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
- FILL IN THE BLANKS
- LONG ANSWER QUESTIONS - I
- LONG ANSWER QUESTIONS - II
- MULTIPLE CHOICE QUESTIONS
- NCERT TEXTBOOK EXERCISES
- SELF ASSESSMENT TEST (SECTION A (FILL IN THE BLANKS))
- SELF ASSESSMENT TEST (SECTION A (MULTIPLE CHOICE QUESTIONS))
- SELF ASSESSMENT TEST (SECTION C )
- SHORT ANSWER QUESTIONS
- TRUE OR FALSE
- VERY SHORT ANSWER QUESTIONS