Complete Solutions to PROBLEMS of chapter FORCE AND MOTION-II of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FORCE AND MOTION-II |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
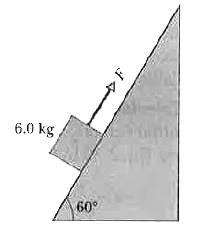
Figure 6-28 shows a 6.0 kg block on a `60^(@)` ramp with a coefficient of static friction of 0.60. A force `vecF` is applied up the ramp. What magnitude of that force puts the block on the verge of sliding down the ramp? 6.0 kg
View SolutionIn a pickup game of dorm shuffleboard, students crazed by final exams use a broom to propel a calculus book along the dorm hallway. If the 3.5 kg book is pushed from rest through a distance of 1.20 m by the horizontal 25 N force from the broom and then has a speed of 1.75 m/s, what is the coefficient of kinetic friction between the book and floor?
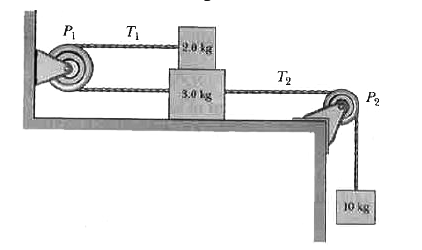
View SolutionIn Fig. 6-29, a 2.0 kg block is placed on top of a 3.0 kg block, which lies on a frictionless surface. The coefficient of kinetic friction between the two blocks is 0.30, they are connected via a pulley and a string. A hanging block of mass 10 kg is connected to the 3.0 kg block via another pulley and string. Both strings have negligible mass and both pulleys are frictionless and have negligible mass. When the assembly is released, what are (a) the acceleration magnitude of the blocks, (b) the tension in string 1, and (c) the tension in string 2?
View SolutionTwo block `M` and and m are arranged as shows in figure . If `M = 50 kg` then determine the minimum and maximum value of mass of block the heavy block `M` stationary
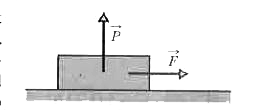
View SolutionA 2.5 kg block is initially at rest on a horizontal surface. A horizontal force `vecF` of magnitude 6.0 N and a vertical force `vecP` are then applied to the block (Fig. 6-31). The coefficients of friction for the block and surface are `mu = 0.40 and mu = 0.25`. Determine the magnitude of the frictional force acting on the block if the magnitude of `vecP` is (a) 8.0 N. (b) 10 N, and (c) 12 N
View SolutionA body of mass 2 kg is moving on the ground comes to rest after some time. The coefficient of kinetic friction between the body and the ground is 0.2. The etardation in the body is
View SolutionThe mysterious sliding stones. Along the remote Racetrack Play a in Death Valley, California, stones sometimes gouge out prominent trails in the desert floor, as if the stones had been migrating (Fig. 6-32). For years curiosity mounted about why the stones moved. One explanation was that strong winds during occasional rainstorms would drag the rough stones over ground softened by rain. When the desert dried out, the trails behind the stones were hardbaked in place. According to measurements, the coefficient of kinetic friction between the stones and the wet playa ground is about 0.80. What horizontal force must act on a 20 kg stone (a typical mass) to maintain the stone's motion once a gust has started it moving? (Story continues with Problem 34.)

View SolutionA 3.5 kg block is pushed along a horizontal floor by a force `vecF` of magnitude 15 N at an angle `theta = 40^(@)` with the horizontal (Fig. 6-33). The coefficient of kinetic friction between the block and the floor is 0.25. Calculate the magnitudes of (a) the frictional force on the block from the floor and (b) the block's acceleration.

View SolutionIn Fig. 6-34 a block of weight W experiences two applied forces, each of magnitude W/2. What coefficient of static friction between the block and the floor puts the block on the verge of sliding?

View SolutionIn about 1915, Henry Sincosky of Philadelphia suspended himself from a rafter by gripping the rafter with the thumb of each hand on one side and the fingers on the opposite side (Fig. 6-35). Sincosky's mass was 79 kg. If the coefficient of static friction between hand and rafter was 0.70, what was the least magnitude of the normal force on the rafter from each thumb or opposite fingers? (After suspending himself, Sincosky chinned himself on the rafter and then moved hand-over-hand along the rafter. If you do not think Sincosky's grip was remarkable, try to repeat his stunt.)

View SolutionA crate of mass 20 kg is sliding across a wooden floor. The coefficient of kinetic friction between the crate and the floor is 0.3.
Determine the magnitude of the friction force acting on the crate.
View SolutionFigure 6-36 shows the cross section of a road cut Joint with ice into the side of a mountain. The solid line AA' represents a weak bedding plane along which sliding is possible. Block B directly above the highway is separated from uphill rock by a large crack (called a joint), so that only friction between the block and the bedding plane prevents sliding. The mass of the block is `1.5 xx 10^(7)kg`, the dip angle `theta` of the bedding plane is `24^(@)`, and the coefficient of static friction between block and plane is 0.63. (a) Show that the block will not slide under these circumstances. (b) Next, water seeps into the joint and expands upon freezing, exerting on the block a force F parallel to AA'. What minimum value of force magnitude `vecF` will trigger a slide down the plane?

View SolutionIn Fig. 6-37, a block of mass m = 5.0 kg is at rest on a ramp. The coefficient of static friction between the block and ramp is not known. Find the magnitude of the net force exerted by the ramp on the block.

View SolutionA small block of mass `m` is projected on a larger block of mass `10 m` and length `l` with a velocity `v` as shown in the figure. The coefficient of friction between the two block is `mu_(2)` while that between the lower block and the ground is `mu_(1)`. Given that `mu_(2) gt 11 mu_(1)`.

(a) Find the minimum value of `v`, such that the mass `m` falls off the block of mass `10 m` .
(b) If `v` has minimum value, find the time taken by block `m` to do so.
View SolutionIn Fig. 6-29, a force `vecP` acts on a block weighing 45 N. The block is initially at rest on a plane inclined at angle `theta= 15^(@)` to the horizontal. The positive direction of the r axis is up the plane. Between block and plane, the coefficient of static friction is `mu_(s) = 0.50` and the coefficient of kinetic friction is `mu_(k) = 0.34`. In unitvector notation, what is the frictional force on the block from the plane when `vecP` is (a)`(-5.0 N)hati, (b) (-8.0 N)hati, and (c) (-15 N)hati`?

View SolutionYou testify as an expert witness in a case involving an accident in which car A slid into the rear of car B, which was stopped at a red light along a road headed down a hill (Fig. 6-40). You find that the slope of the hill is `theta= 1.0^(@)`, that the cars were separated by distance d = 30.0 m when the driver of car A put the car into a slide (it lacked any automatic anti-brake-lock system), and that the speed of car A at the onset of braking was `v=18.0` m/s. With what speed did car A hit car B if the coefficient of kinetic friction was (a) 0.60 (dry road surface) and (b) 0.10 (road surface covered with wet leaves)? mu Figure 6-20 Problem 16

View SolutionA 12 N horizontal force `vecF` pushes a block weighing 5.0 N against a vertical wall (Fig. 6-41). The coefficient of static friction between the wall and the block is 0.00, and the . coefficient of kinetic friction is 0.40. Assume that the block is not moving initially. (a) Will the block move? (b) In unit-vector notation, what is the force on the block from the wall?

View SolutionIn Fig. 6-42, a box of Cheerios (mass `m_(c)= 1.0 kg)` and a box of Wheaties (mass `m_(w) = 3.0 kg)` are accelerated across a horizontal surface by a horizontal force `vecF` applied to the Cheerios box. The magnitude of the frictional force on the Cheerios box is 2.0 N, and the magnitude of the frictional force on the Wheaties box is 3.5 N. If the magnitude of `vecF` is 12 N, what is the magnitude of the force on the Wheaties box from the Cheerios box?

View SolutionIn Fig. 6-43, a 15 kg sled is attached to a 2.0 kg sand box by a string of negligible mass, wrapped over a pulley of negligible mass and friction. The coefficient of kinetic friction between the sled and table top is 0.040. Find (a) the acceleration of the sled and (b) the tension of the string.
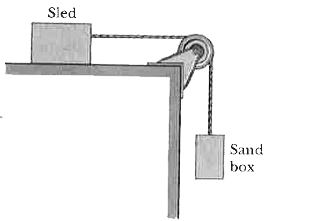
View SolutionIn Fig. 6-44a, a sled is held on an inclined plane by a cord pulling directly up the plane. The sled is to be on the verge of moving up the plane. In Fig. 6-44h, the magnitude F required of the cord's force on the sled is plotted versus a range of values for the coefficient of static friction u between sled and plane: `F_(1) 2.0 N, F_(2)= 5.0 N, and mu_(2) = 0.25`. At what angle `theta` is the plane inclined?
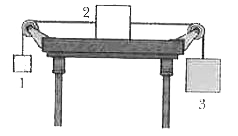
View SolutionWhen the three blocks in Fig. 6-45 are released from rest, they accelerate with a magnitude of 0.500 m/s2 Block 1 has mass M, block 2 has 2M, and block 3 has 2M. What is the coefficient of kinetic friction between block 2 and the table?
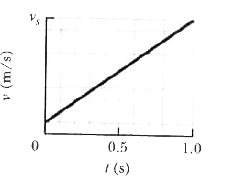
View SolutionA 4.10 kg block is pushed along a floor by a constant applied force that is horizontal and has a magnitude of 50.0 N. Figure 6-46 gives the block's speed v versus time t as the block moves 0.5 1.0 along an x axis on the floor. The scale of the figure's vertical axis is set by `v_(s) = 5.0` m/s. What is the coefficient of kinetic friction between the block and the floor?
View SolutionFigure 6-47 shows three crates being pushed over a concrete floor by a horizontal force F of magnitude 425 N. The masses of the crates are `m_(1) = 30.0 kg, m_(2)= 10.0 kg, and m_(3) = 20.0 kg` The coefficient of kinetic friction between the floor and each of the crates is 0.700. (a) What is the magnitude `F_(32)` of the force on crate 3 from crate 2? (b) If the crates then slide onto a polished floor, where the coefficient of kinetic friction is less than 0.700, is magnitude `F_(32)` more than, less than, or the same as it was when the coefficient was 0.700?

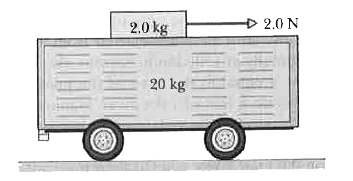
View SolutionIn Fig. 6-48, a 2.0 kg block lies on a 20 kg trolley that can roll across a floor on frictionless bearings. Between the block and the trolley, the coefficient of kinetic friction is 0.20 and the coefficient of static friction is 0.25. When a horizontal 2.0 N force is applied to the block, what are the magnitudes of (a) the frictional force between the block and the trolley and (b) the acceleration of the trolley?
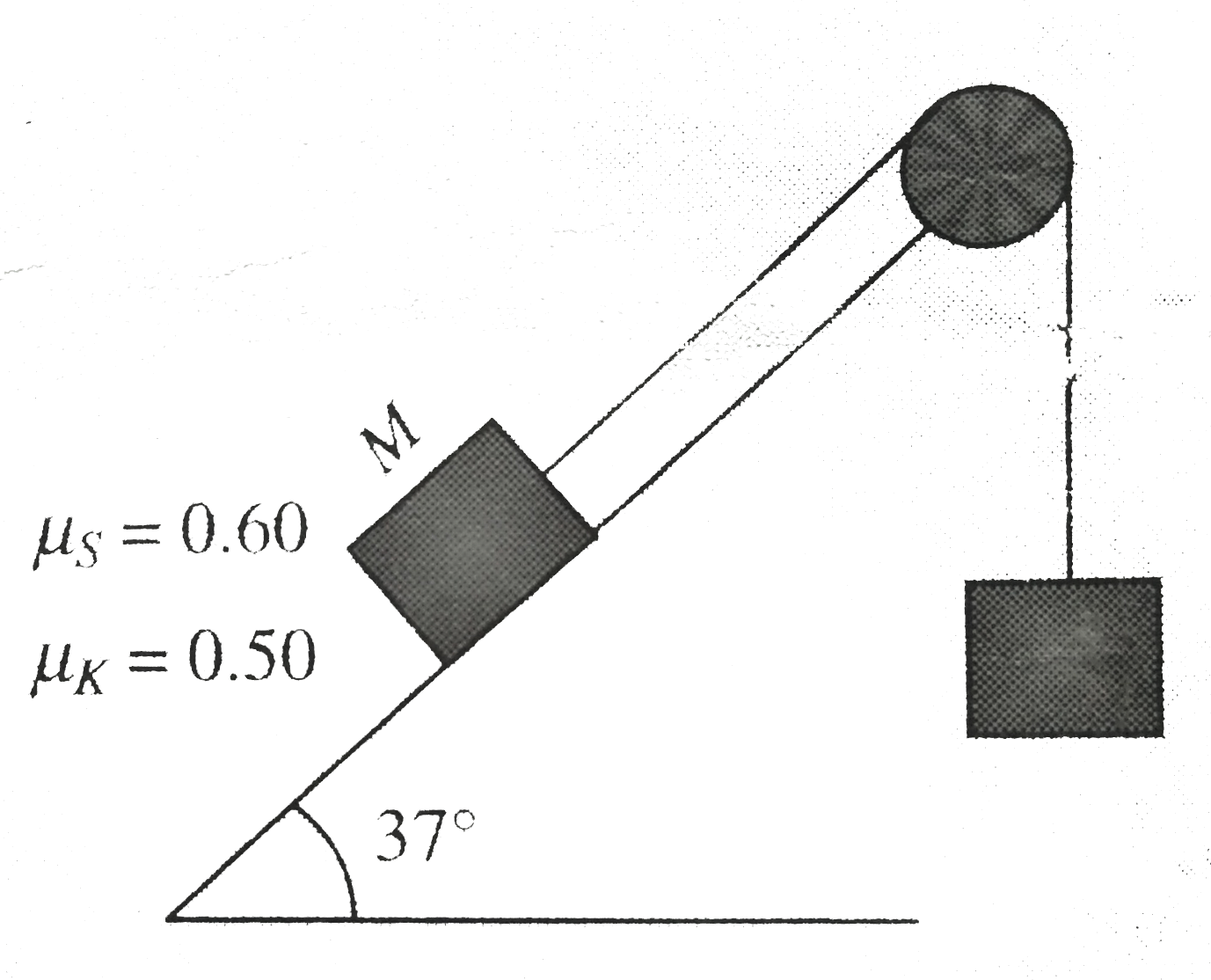
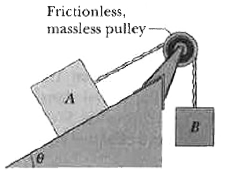
View SolutionIn Fig. 6-49, two blocks are connected over a pulley. The mass of block A is 15 kg, and the coefficient of kinetic friction between A and the incline is 0.20 Angle `theta` of the incline is `30^(@)`. Block A slides down the incline at constant speed. What is the mass of block B?
View SolutionIn Fig. 6-50, block A of mass 2.0 kg, block B of 3.0kg, and block Cof 6.0 kg are connected by strings of negligible mass that run over pulleys of negligible mass and friction. The coef ficient of kinetic friction between block B and the table top is 0.40. When the system is released, the blocks move. What is the magnitude of their acceleration?

View SolutionA toy chest and its contents have a combined weight of 200 N. The coefficient of static friction between toy chest and floor is 0.47. The child in Fig. 6-51 attempts to move the chest across the floor by pulling on an attached rope. (a) If `theta` is `42^(@)` what is the magnitude of the force F that the child must exert on the rope to put the chest on the verge of moving? (b) Write an expression for the magnitude Frequired to put the chest on the verge of moving as a function of the angle `theta`. Determine (c) the value of `theta` for which F is a minimum and (d) that minimum magnitude.

View SolutionIn Fig. 6-52, two blocks, in contact, slide down an inclined plane AC of inclination `30^(@)` . The coefficient of kinetic friction between the 2.0 kg block and the incline is `u_(1)=0.20` and that between the 4.0 kg block and the incline is `mu_(2)=0.30`. Find the magnitude of the acceleration.

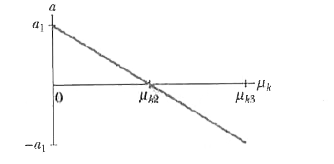
View SolutionA block is pushed across a floor by a constant force that is applied at downward angle `theta` (Fig. 6-33). Figure 6-53 gives the acceleration magnitude a versus a range of values for the coefficient of kinetic friction `mu_(k)` between block and floor: `a_(1) = 3.0 m//s^(2) mu_(2) = 0.20, and mu_(k3) = 0.40`. What is the value of `theta` ?
View SolutionIn Fig. 6-54, a slab of mass `m_(1) = 40` kg rests on a frictionless floor, and a block of mass `m_(2) = 12` kg rests on top of the slab. Between block and slab, the coefficient of static friction is 0.60, and the coefficient of kinetic friction is 0.40. A horizontal force `vecF` of magnitude 120 N begins to pull directly on the block, as shown. In unit-vector notation, what are the resulting accelerations of (a) the block and (b) the slab?

View SolutionA water droplet 4.0 mm in diameter is falling with a speed of 10 km/h at an altitude of 20 km. Another droplet 6.0 mm in diameter is falling at 25% of that speed and at 25% of that altitude. The density of air at 20 km is `0.20 kg//m^(3)`and that at 5.0 km is `0.70 kg//m^(3)` Assume that the drag coefficient C is the same for the two drops. Find the ratio of the drag force on the higher drop to that on the lower drop.
View SolutionContinuation of Problem z Now assume that Eq, 6-29 gives the magnitude of the air drag force on the typical 20 kg stone, which presents to the wind a vertical crosssectional area of 0.040 m2 and has a drag coefficient C of 0.80.Take the air density to be `1.21 kg//m^(3)` and the coefficient of kinetic friction to be 0.80. (a) In kilometers per hour, what wind speed Valong the ground is needed to maintain the stone's motion once it has started moving? Because winds along the ground are retarded by the ground, the wind speeds reported for storms are often measured at a height of 10 m. Assume wind speeds are 2.00 times those along the ground. (b) For your answer to (a), what wind speed would be reported for the storm? (c) Is that value reasonable for a high speed wind in a storm?
View SolutionAssume Eq. 6-29 gives the drag force on a pilot plus ejec-tion seat just after they are ejected from a plane traveling horizontally at 1300 km/h. Assume also that the mass of the seat is equal to the mass of the pilot and that the drag coefficient is that of a sky diver. Making a reasonable guess of the pilot's mass and using the appropriate v, value from Table 6-2, estimate the magnitudes of (a) the drag force on the pilot + seat and (b) their horizontal deceleration (in terms of g), both just after ejection. (The result of (a) should indicate an engineering requirement: The seat must include a protective barrier to deflect the initial wind blast away from the pilot's head.)
View Solution
PROBLEMS questions and complete solutions for chapter FORCE AND MOTION-II of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12