Complete Solutions to PROBLEMS of chapter MOTION IN TWO AND THREE DIMENSIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN TWO AND THREE DIMENSIONS |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The position vector for an electron is `vecr=(6.0m)hati-(4.0m)hatj+(3.0m)hatk`. (a) Find the magnitude of `vecr`.
View SolutionA watermelon seed has the following coordinates: x = -5.0 m, y = 9.0 m, and z = 0 m. Find its position vector (a) in unit-vector notation and as (b) a magnitude and ( c) an angle relative to the positive direction of the x axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the xyz coordinates (3.00 m, 0 m, 0 m), what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive x direction?
View SolutionAn elementary particle is subjected to a displacement of `Deltavecr=2.0hati-4.0hatj+8.0hatk`, ending with the position vector `vecr=4.0hatj-5.0hatk`, in meters. What was the particle's initial position vector?
View SolutionThe minute hand of a wall clock measures 12 cm from its tip to the axis about which it rotates. The magnitude and angle of the displacement vector of the tip are to be determined for three time intervals. What are the (a) magnitude and (b) angle from a quarter after the hour to half past, the ( c) magnitude and (d) angle for the next half hour, and the (e) magnitude and (f) angle for the hour after that?
View SolutionA train at a constant 60.0 km/h moves east for 40.0 min, then in a direction `50.0^(@)` east of due north for 20.0 min, and then west for 50.0 min. What are the (a) magnitude and (b) angle of its average velocity during this trip?
View SolutionAn electron's position is given by `vecr=3.00hati-4.00t^(2)hatj+2.00hatk`, with t in seconds and `vecr` in meters. (a) In unit-vector notation, what is the electron's velocity `vecr(t)`? At t = 3.00 s, what is `vecv` (b) in unitvector notation and as ( c) a magnitude and (d) an angle relative to the positive direction of the x axis?
View SolutionIn a particle accelerator, the position vector of a particle is initially estimated as `vecr=6.0hati-7.0hatj+3.0hatk` and after 10 s, it is estimated to be `vecr=-3.0hati+9.0hatj-3.0hatk`, all in meters. In unit vector notation, what is the average velocity of the particle?
View SolutionA plane flies 483 km east from city A to city B in 48.0 min and then 966 km south from city B to city C in 1.50 h. For the total trip, what are the (a) magnitude and (b) direction of the plane's displacement, the (c ) magnitude and (d) direction of its average velocity, and (e) its average speed?
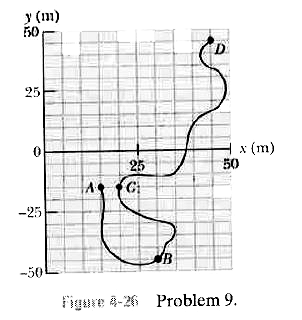
View SolutionFigure 4-26 gives the path of a squirrel moving about on level ground, from point A (at time t = 0), to points B (at t = 5.00 min), C (at t = 10.0 min), and finally D (at t = 15.0 min). Consider the average velocities of the squirrel from point A to each of the other three points. Of them, what are the (a) magnitude and (b) angle of the one with the least magnitude and the ( c) magnitude and (d) angle of the one with the greatest magnitude?
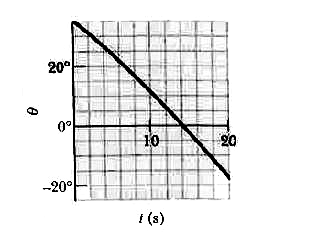
View SolutionThe position vector `vecr=5.00thati+(et+ft^(2))hatj` locates a particle as a function of time t. Vector `vecr` is in meters, t is in seconds, and factors e and f are constants. Figure 4-27 gives the angle `theta` of the particle's direction of travel as a function of t (`theta` is measured from the positive x direction). What are (a) e and (b) f, including units?
View SolutionA particle that is moving in an xy plane has a position vector given by `vecr=(3.00t^(3)-6.00t)hati+(7.00-8.00t^(4))hatj`, where `vecr` is measued in meters and t is measured in seconds. For t = 3.00 s, in unitvector notation, find (a) `vecr`, (b) `vecv`, and ( c) `veca`. (d) Find the angle between the positive direction of the x axis and a line that is tangent to the path of the particle at t = 3.00 s.
View SolutionAt one instant a bicyclist is 30.0 m due east of a park's flagpole, going due south with a speed of 10.0 m/s. Then 30.0 s later, the cyclist is 40.0 m due north of the flagpole, going due east with a speed of 10.0 m/s. For the cyclist in this 30.0 s interval, what are the (a) magnitude and (b) direction of the displacement, the ( c) magnitude and (d) direction of the average velocity, and the (e) magnitude and (f) direction of the average acceleration?
View SolutionAn object moves in such a way that its position (in meters) as a function of time (in seconds) is `vecr=hati+3t^(2)hatj+thatk`. Give expressions for (a) the velocity of the object and (b) the acceleration of the object as functions of time.
View SolutionFrom the origin, a particle starts at t = 0 s with a velocity `vecv=7.0hatim//s` and moves in the xy plane with a constant acceleration of `veca=(-9.0hati+3.0hatj)m//s^(2)`. At the time the particle reaches the maximum x coordinate, what is its (a) velocity and (b) position vector?
View SolutionThe velocity `vecv` of a particle moving in the xy plane is given by `vecv=(6.0t-4.0t^(2))hati+8.0hatj`, with `vecv` in meters per second and `t(gt0)` in seconds. (a) What is the acceleration when t = 2.5 s? (b) When (if ever) is the acceleration zero ? (c) When (if ever) is the velocity zero? (d) When (if ever) does the speed equal 10 m/s?
View SolutionA motorbike starts from the origin and moves over an xy plane with acceleration components `a_(x)=6.0m//s^(2)anda_(y)=-3.0m//s^(2)`. The initial velocity of the motorbike has components `v_(0x)=12.0m//sandv_(0y)=18.0m//s`. Find the velocity of the motorbike, in unt-vector notation, when it reaches its greatest y coordinate.
View SolutionThe acceleration of a particle moving only on a horizontal xy plane is given by `veca=3thati+4thatj`, where `veca` is in meters per secondsquared and t is in seconds. At t = 0, the position vector `vecr=(20.0m)hati+(40.0m)hatj` locates the particle, which then has velocity vector `vecv=(5.00m//s)hati+(2.00m//s)hatj`. At t = 4.00 s, what are (a) its position vector in unit-vector notation and (b) the angle between its direction of travel and the position direction of the x axis?
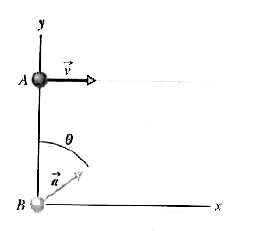
View SolutionIn Fig. 4-28, particle A moves along the line y = 30 m with a constant velocity `vecv` of magnitude 3.0m/s and parallel to the x axis. At the instant particle A passes the y axis, particle B leaves the origin with a zero initial speed and a constant acceleration `veca` of magnitude `0.40m//s^(2)`. What angle `theta` between `veca` and the positive direction of the y axis would result in a collision?
View SolutionA small ball rolls horizontally off the edge of a tabletop that is 1.50 m high. It strikes the floor at a point 1.52 m horizontally from the table edge. (a) How long is the ball in the air? (b) What is its speed at the instant it leaves the table?
View SolutionA shell, which is initially located at a distance of 40.4 m above a horizontal plane, is fired horizontally with a muzzle velocity of 285 m/s to strike a target on the horizontal plane. (a) How long does the projectile remain in the air? (b) At what horizontal distance from the firing point does the shell strike the plane? What are the magnitudes of the (c ) horizontal and (d) vertical components of its velocity as it strikes the ground?
View SolutionA stone is catapulted at time t = 0, with an initial velocity of magnitude 18.0 m/s and at an angle of `40.0^(@)` above the horizontal. What are the magnitude of the (a) horizontal and (b) vertical components of its displacement from the catapult site at t = 1.10 s? Repeat for the ( c) horizontal and (d) vertical components at t = 1.80 s, and for the (e) horizontal and (f) vertical components at t = 5.00 s.
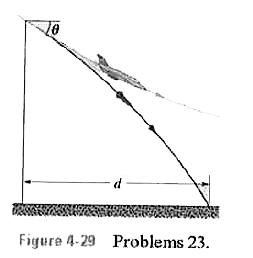
View SolutionA certain airplane has a speed of 290.0 km/h and is diving at an angle of `theta=30.0^(@)` below the horizontal when the pilot releases a radar decoy. The horizontal distance between the release point and the point where the decoy strikes the ground is d = 700 m. (a) How long is the decoy in the air? (b) How high was the release point?
View SolutionIn Fig. 4-30 a stone is projected at a cliff of height h with an initial speed of 42.0 m/s directed at angle `theta_(0)=60.0^(@)` above the horizontal. The stone strikes at A, 5.50 s after launching. Find (a) the height h of the cliff, (b) the speed of the stone just before impact at A, and ( c) the maximum height H reached above the ground.

View SolutionA projectile's launch speed is 6.00 times that of its speed at its maximum height. Find the launch angle `theta_(0)`.
View SolutionA soccer ball is kicked from the ground with an initial speed of 21.3 m/s at an upward angle of `45^(@)`. A player 55 m away in the direction of the kick starts running to meet the ball at that instant. What must be his average speed if he is to meet the ball just before it hits the ground?
View SolutionYou throw a ball toward a wall at speed 25.0 m/s and at angle `theta_(0)=40.0^(@)` above the horizontal. The wall is distance d = 22.0 m from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and ( c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?
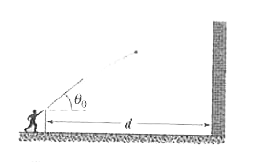
View SolutionA defense air force plane, diving with constant speed at an angle of `52.0^(@)` with the vertical, drops a shell at an altitude of 720 m. The shell reaches the ground 6.00 s after its release. (a) What is the speed of the plane? (b) How far does the shell travel horizontally during its flight? What are the ( c) horizontal and (d) vertical components of its velocity just before reaching the ground? Assume an x axis in the direction of the horizontal motion and an upward y axis.
View SolutionA rifle that shoots bullets at 460 m/s is to be aimed at a traget 45.7 m away. If the center of the target is level with the rifle, how high above the target must the rifle barrel be pointed so that the bullet hits dead center?
View SolutionA golf ball is struck at ground level. The speed of the golf ball as a function of the time is shown in, where t = 0 at the instant the ball is struck. The scaling on the vertical axis is set by `v_(a)=19m//sandv_(b)=31m//s`. (a) How far does the golf ball travel horizontally before returning to ground level? (b) What is the maximum height above ground level attained by the ball?
View SolutionIn a ball is thrown leftward from the left edge of the roof, at height h above the ground. The ball hits the ground 1.50 s later, at distance d = 25.0 m from the building and at angle `theta=60.0^(@)` with the horizontal. (a) Find h. (Hint: One way is to reverse the motion, as if on video.) What are the (b) magnitude and ( c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal?

View SolutionUpon spotting an insect on a twig overhanging water, an archer fish squirts water drops at the insect to knock it into the water. Although the insect is located along a straightline path at angle `phi` and distance d, a drop must be launched at a different angle `theta_(0)` if its parabolic path is to intersect the insect. If `phi=36.0^(@)` and d = 0.900 m. what launch angle `theta_(0)` is required for the drop to be at the top of the parabolic path when it reaches the insect?

View SolutionA golfer hits a golf ball into the air over level ground. The velocity of the ball at a height of 10.3 m is `vecv=(8.6hati+7.2hatj)m//s`, with `hati` horizontal and `hatj` upward. Find (a) the maximum height of the ball and (b) the total horizontal distance traveled by the ball. What are the ( c) magnitude and (d) angle (below the horizonatl) of the balls velocity just before it touches the ground?
View SolutionA baseball leaves a pitcher's hand horizontally at a speed of 153 km/h. The distance to the batter is 18.3 m. (a) How long does the ball take to travel the first half of that distance? (b) The second half? (c ) How far does the ball fall freely during the first half? (d) During the second half? (e) Why aren't the quantities in ( c) and (d) equal?
View SolutionA batter hits a pitched ball when the centre of the ball is 1.22 m above the ground. The ball leaves the bat at an angle of `45^(@)` with the ground. With that launch, the ball should have a horizontal range (returning to the launch level) of 107 m. (a) Does the ball clear a 7.32-m-high fence that is 9.75 m horizontally from the launch point? (b) At the fence, what is the distance between the fence top and the ball center?
View SolutionA ball is thrown up onto a roof, landing 4.50 s later at height h = 20.0 m above the release level. The ball's path just before landing is angled at `theta=60.0^(@)` with the roof. (a) Find the horizontal distance d it travels. What are the (b) magnitude and ( c) angle (relative to the horizontal) of the ball's initial velocity?
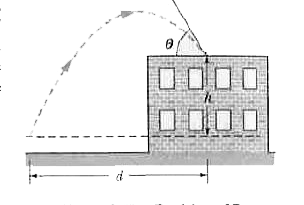
View SolutionTwo seconds after being projected from ground level, a projectile is displaced 40 m horizontally and 58 m vertically above its launch point. What are the (a) horizontal and (b) vertical components of the initial velocity of the projectile? (c ) At the instant the projectile achieves its maximum height above ground level, how far is it displaced horizontally from the launch point?
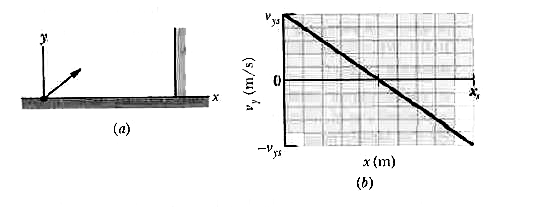
View SolutionA ball is to be shot from level ground toward a wall at distance x. Figure 4-36b shows the y component `v_(y)` of the ball's velocity just as it would reach the wall, as a function of that distance x. The scaling is set by `v_(ys)=5.0m//sandx_(s)=20m`. What is the launch angle?
View SolutionA baseball is hit at a height h = 1.00 m and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall. 4.00 s later, at distance D = 50.0 m farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and ( c) angle (relative to the horizontal) of the ball's velocity just after being hit? (d) How high is the wall?
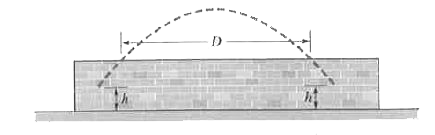
View SolutionA ball is to be shot from level ground with a certain speed. Figure 4-38 shows the range R it will have versus the launch angle `theta_(0)`. The value of `theta_(0)` determines the flight time, let `t_(max)` represent the maximum flight time. What is the least speed the ball will have during its flight if `theta_(0)` is chosen such that the flight time is `0.500t_(max)`?
View SolutionA cameraman on a pickup truck is traveling westward at 20 km/h while he records a cheetah that is moving westward 30 km/h faster than the truck. Suddenly, the cheetah stops, turns, and then runs at 45 km/h east-ward, as measured by a suddenly nervous crew member who stands alongside the cheetah's path. The change in the animal's velocity takes 2.0 s. What are the (a) magnitude and (b) direction of the animal's acceleration according to the cameraman and the ( c) magnitude and (d) direction according to the nervous crew member?
View SolutionA boat is traveling upstream in the positive direction of an x axis at 14 km/h with respect to the water of a river. The water is flowing at 8.2 km/h with respect to the ground. What are the (a) magnitude and (b) direction of the boat's velocity with respect to the ground? A child on the boat walks from front to rear at 6.0 km/h with respect to the boat. What are the ( c) magnitude and (d) direction of the child's velocity with respect to the ground?
View SolutionA suspicious-looking man runs as fast as he can along a moving sidewalk from one end to the other, taking 2.50 s. Then security agents appear, and the man runs as fast as he can back along the sidewalk to his starting point, taking 10.0 s. What is the ratio of the man's running speed to the sidewalk's speed?
View SolutionA rugby player runs with the ball directly toward his opponent's goal, along the positive direction of an x axis. He can legally pass the ball to a teammate as long as the ball's velocity relative to the field does not have a positive x component. Suppose the player runs at speed 3.5 m/s relative to the field while he passes the ball with velocity `vecv_(BP)` relative to himself. If `vecv_(BP)` has magnitude 6.0m/s, what is the smallest angle it can have for the pass to be legal?
View SolutionTwo highways intersect as shown in Fig. 4-39. At the instant shown, a police car P is distance `d_(p)=800m` from the intersection and moving at speed `v_(p)=80km//h`. Motorist M is
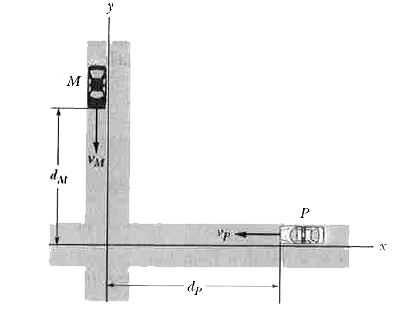
distance `d_(M)=600m` from the intersection and moving at speed `v_(M)=60km//h`. (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-39, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c ) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection?
View SolutionAfter flying for 18 min in a wind blowing 42 km/h at an angle of `20^(@)` south of east, an airplane pilot is over a town that is 55 km due north of the starting point. What is the speed of the airplane relative to the air?
View SolutionA light plane attains an airspeed of 500 km/h. The pilot sets out for a destination 900 km due north but discovers that the plane must be headed `20.0^(@)` east of due north to fly there directly. The plane arrives in 2.00 h. What were the (a) magnitude and (b) direction of the wind velocity?
View SolutionSnow is falling vertically at a constant speed of 8.0 m/s. At what angle from the vertical do the snowflakes appear to be falling as viewed by the driver of a car traveling on a straight, level road with a speed of 50 km/h?
View SolutionIn the overhead view of Fig. 4-40, Jeeps P and B race along straight lines, across flat terrain, and past stationary border guard A. Relative to the guard, B travels at a constant speed of 25.0 m/s, at the angle `theta_(2)=30.0^(@)`. Relative to the guard, P has accelerated from rest at a constant rate of `0.400m//s^(2)` at the angle `theta_(1)=60.0^(@)`. At a certain time during the acceleration, P has a speed of 40.0 m/s. At that time, what are the (a) magnitude and (b) direction of the velocity of P relative to B and the ( c) magnitude and (d) direction of the acceleration of P relative to B?

View SolutionTwo ships, A and B, leave port at the same time. Ship A travels northwest at 24 knots, and ship B travels at 28 knots in a direction `40^(@)` west of south (1 knot = 1 nautical mile per hour, see Appendix D). What are the (a) magnitude and (b) direction of the velocity of ship A relative to B? ( c) After what time will the ships be 160 nautical miles apart? (d) What will be the bearing of B (the direction of B's position) relative to A at that time?
View SolutionShip A is located 4.0 km north and 2.5 km east of ship B. Ship A has a velocity of 22 km/h toward the south, and ship B has a velocity of 40 km/h in a direction `37^(@)` north of east. (a) What is the velocity of A relative to B in unit-vector notation with toward the east? (b) Write an expression (in terms of `hatiandhatj`) for the position of A relative to B as a function of t, where t = 0 when the ships are in the positions described above. ( c) At what time is the separation between the ships least? (d) What is that least separation?
View Solution
PROBLEMS questions and complete solutions for chapter MOTION IN TWO AND THREE DIMENSIONS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12