Complete Solutions to SOLVED EXAMPLES of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| NEW JOYTHI PUBLICATION | SOLVED EXAMPLES |
| Number Of Questions | 67 |
| Academic Year | 2023-24 |
If `P(A) = (7)/(13), P(B) = (9)/(13)` and `P(BnnA) = (4)/(13)` evaluate P(A|B)
View SolutionIf `P(A) = 0.6, P(B) = 0.7` and `P(BuuA) = 0.9` then find P(A|B) and P(B|A)
View SolutionIf P(A) = 0.8, P(B) = 0.5 and P(B|A) = 0.4 Find i. `P(AnnB)` ii. P(A|B) iii. `P(AuuB)`
View SolutionIn a school, there are 1000 students, out of which 430 are girls. It is known that out of 430, 10% of girls study in class XII. What is the probability that a student chosen randomly studies in class XII given that the chosen student is a girl.
View SolutionSuppose 10 cards numbered 1 to 10 are placed in a box and shuffled and one card is drawn at random.
i. If A is the event that the number on the card is even, then write A.
ii. If B is the event that the number on the card is more than 3, find P(A|B)
View SolutionA fair die is thrown twice. Let A denote the event that '4' has appeared atleast once. Let B denote the event that the sum of the outcomes in two trials is 6.
i Write down the set of favourable outcomes for the event A.
ii. Write down the set of favourable outcomes for the events B
iii Compute P(A|B), the conditional probabilityof A given B.
View SolutionA die is thrown three times, A: 4 appears on the third toss, B: 6 and 5 appear respectively on first two tosses. Determine P(A|B)
View SolutionThe probability that a man buying a shirt is 0.2 and that for buying a trouser is 0.3. The probability that he will buy a shirt given that he buys a trouser is 0.4.
i. Find the probability that he will buy both a shirt and a trouser
ii. Find the probability that he will buy a trouser, given that he buys a shirt.
View SolutionConsider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that the die shows a number greater than 4 given that there is atleast one tail.
View SolutionAn urn contains 10 black and 5 white balls. Two balls are drawn from the urn one after the other without replacement. What is the probability that both drawn balls are black?
View SolutionTwo balls are drawn at random withreplacement from a box containing 10 black and 8 red balls. Find the probability that
a. Both the balls are red.
b. One of them is black and the other is red
View SolutionA card is drawn from a well shuffled pack of cards.
i. What is the probability that the card drawn is an ace?
ii. If the first card is not replaced and a second card is drawn, what is the probability that both are aces
iii. If the first card is replaced and a second card is drawn, what is the probability that both are aces?
View SolutionThree cards are drawn successively, without replacement from a pack of 52 well shuffled cards. What is the probability that first two cards are kings and the third card is an ace?
View SolutionA box oforanges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones willI be approved for sale.
View SolutionLet A and B be two independent events such that `P(A)= (1)/(7) , P(B) = (1)/(5)` Find
i. `P(AnnB)`
ii. `P(AuuB)`
View SolutionLet E and F be events with `P(E) = (3)/(5), P(F)= (3)/(10)` and `P(EnnF)= (1)/(5)` Are E and F independent?
View SolutionTwo events E and F are such that P(E) = 0.6, P(F) = 0.2 and P(EuuF) = 0.68. Are E and F are independent?
View SolutionGiven that the events A and B are such that `P(A) =(1)/(2) , P(AuuB) = (3)/(5)` and P(B) = p. Find p if they are (i) mutually exclusive, (ii) independent.
View SolutionA die is thrown. E is the event "the number appearing us a multiple of 3" and F be the event "the number appearing is even". Find whether E and F are independent.
View SolutionAn unbaised die is thrown twice. Let the event A be "odd number on the first throw" and B be the event odd number on the second throw. Check the independence of the events A and B
View SolutionThree coins are tossed simultaneously. Let the event E 'three heads or three tails', F 'at least two heads' and G 'at most two heads'. Of the pairs (E, F), (E, G) and (F, G), which are independent? which are dependent.
View SolutionIf A and B are two independent events, then the probability of occurrence of at least one of A and B is given by 1- P(A') P(B').
View SolutionTwo balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that
i both balls are red.
ii. first ball is black and second is red.
ii. one of them black and other is red.
View SolutionA and B try to solve a problem independently Probability that A solves the problem is `(1)/(3)` and that B solves the problem is `(1)/(4)`. Find the probability that
i. Both of them solve the problem.
ii. The problem is solved.
View SolutionA and B throw a die alternatively till one of them gets a '6' and wins the game. Find their respective probabilities of winning, if A starts first.
View SolutionFind the probability of drawing a one-rupeee coin from a purse with two compartments one of which contains 3 fifty paise coins and 2 one rupee coins and other contains 2 fifty paise coins and 3 one-rupee coins
View SolutionA person has undertaken a construetion job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time it there is no strike and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
View SolutionBagI contains 3 red and 4 black balls while another Bag II contains 5 red and 6 black balls. One ball is drawn at random from one ofthe bags and it is found to be red. Find the probability that it was drawn from Bag II.
View SolutionThere are two identical boxes. Box I contains 5 red and 4 black balls, while Box II contains 3 red and 3 black balls. A person chosen a box at random and takes out a ball
a. Find the probability that the ball drawn is red.
b. If the ball drawn is black, what is the probability that it is drawn from Box II.
View SolutionTwo balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that
a. Both the balls are red.
b. One of them is black and the other is red.
View SolutionSuppose that the reliability of a HIV test is specified as follows. Of people having HIV, 90% of the test detect the diséase but 10% go undetected. Of people free of HIV, 99% of the test judged HIV (-ve) but 1% are diagnosed as showing HIV (+ ve). From a large population of which 0.1% have HIV, one person is selected at random, given the HIV test, and the pathologist report him/her as HIV (+ve) What is the probability that the person actually has HIV?
View SolutionA man speaks truth 3 out of 4 times. He throws a die and reports that it is a six. What is the probability that is a six?
View SolutionIf a machine is correctly set up, it produces 90% acceptable items. If it is incorrectly set up, it produces only 40% acceptable items. Past experience shows that 80% of the set ups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly set up.
View SolutionGiven three idential boxes I, II and IIl each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in box III, there is one gold coin and one silver coin. A person chooses a box at random and takes out a coin. If the coin is gold, what is the probability that the other coin in the box is also gold.
View SolutionIn a factory which manufactures bolts, machine A, B and C manufacture respectively 25%, 35% and 45% of the bolts. Of their outputs 5, 4 and 2 percent are respectively defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that if is manufactured by machine B?
View SolutionA doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by train, bus, scooter or by other means of transport are respectively `(3)/(10),(1)/(5),(1)/(10)` and `(2)/(5)` and. The probabilities that he will be late are `(1)/(4), (1)/(3)` and `(1)/(12)` and if he comes by train, bus and scooter respectively, but if he comes by other means of transport, then he will not be late. When he comes, he is late. What is the probability that he comes by train?
View SolutionColoured balls are distributed in four boxes as shown in the following table.
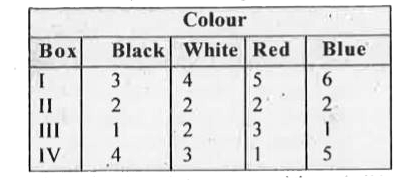
A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black. What is the probability that ball drawn is from the box III?
View SolutionA bag contains 2 white and 1 red ball. One ball is drawn át random and then put back in the box after noting its colour. The process is repeated again. If X denotes the number of red balls recorded in the two draws, describe X.
View SolutionA person plays a game of tossing a coin thrice. For each head, he is given by ₹ 2 by the organiser of the game and for each tail, he has to pay ₹ 1.50 to the organiser. Let X denote the amount gained or lost by the person. Show that X is a random variable and exhibit as a function of the sample space of the experiment.
View SolutionFind the probability distribution of the number of heads in three tosses of a fair coin.
View SolutionFind the probability distribution of the number of heads in three tosses of a fair coin.
View SolutionTwo cards are drawn successively with replacement from a pack of 52 cards. Find the probability distribution of the number of aces.
View SolutionFind the probability distribution of number of doublets in three throws of a pair of dice.
View SolutionA coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.
View SolutionFive defective bulbs are accidentally mixed with 20 good ones. It is not possible to just look at a bulb and tell whether or not it is defective. Find the probability distribution of the number of defective bulbs if 3 bulbs are drawn at random.
View SolutionA random variable X has the following probability distribution.
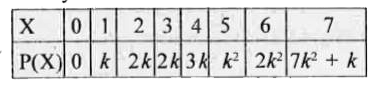
i. k, ii. P(`X lt 3`) iii. P(`Xgt6`) iv. (P(`0lt X lt 3`)
View SolutionLet X denote the number of hours you study during a randomly selected school day. The probability that X can take the values x, has the following form, where k is some unknown constant.
`P(X=x)={{:(0.1,",",x=0),(kx,",","x=1 or 2"),(k(5-x),",","X=3 or 4 "),(0,",","otherwise"):}`
i. Find the value of k
ii. What is the probability that you study atleast two hours? Exactly 2 hours? Atmost 2 hours?
View SolutionProbability distribution of the random variable X is given in the table

i. Find `x_(i)p_(i) i=0, 1,2,3,4`
ii. Find the mean of X.
View SolutionA random variable X has the following prob- ability distribution

i. Find the value of k.
ii. Find P(`1 lt X lt 4`).
ii. Find the mean of the random variable X.
View SolutionA pair of dice is thrown and the random variable X is defined as the sum of numbers that appear on the two dice. Find the mean or expectation of X.
View SolutionIn a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he `"wins" // "loses"`.
View SolutionFind the mean and variance of the number obtained on the throw of an unbaised die.
View SolutionTwo cards are drawn simultaneously from a well shuffled pack of 52 cards. Find the mean, variance and standard deviation of the number of kings.
View SolutionThe probability distribution of a random variable X taking values 1, 2, 3, 4, 5 is given
a. find the value of p .
b. Find the mean of X
c. Find the variance of X
View SolutionThe probability distribution of a randoin variable X is given below

i. Find k.
ii. Find the variance of the random variable
View SolutionSix balls are drawn successively from an urn containing 7 red and 9 black balls. Tell whether or not the trials of drawing balls are Bernoulli trials when after each draw the ball drawn is
i. replaced
ii. not replaced in the urn.
View SolutionIf a fair coin is tossed 10 times, find the probability of
i. exactly six heads
ii atleast six heads
iii atmost six heads
View SolutionTen eggs are drawn successively with replacement from a lot containing 10% defective eggs. Find the· probability that there is atleast one defective egg.
View SolutionA die is tossed thrice. Find the probability of getting an odd number at least once.
View SolutionA coin is tossed 4 times
i. Find the probability of getting exactly 3 heads
ii. Find the probability of getting atleast 3 heads
iii. Find the probaility of getting utmost 3 heads
View SolutionA fair die is thrown thrice. Getting l or 6 is considered as a success.
i. Find p and q, the probability of success and failure respectively in any one trial.
ii. Obtain the probability distribution of the successes.
View Solutionsuppose X has a binomial distribution B(`6, (1)/(2)`) . Show that X = 3 is the most likely outcome.
View SolutionA binomial random variable X ·satisfies the reiation 9P(X = 4) = P(X =2) when n= 6. Find the parameter p.
View SolutionThe probability of a shooter hitting a target `(3)/(4)` How many minimum number of times must he/she fire so that the probability of hitting the target atleast once is more than 0.99?
View SolutionFind the mean of the Binomial distribution B`(4, (1)/(3))`
View SolutionThe mean and variance of a Binomial distribution X are 6 and `(12)/(5)` respectively.
i. Find the parameters n and p of X
ii. Find P(`X ge 1`) given `(0.4)^(10)= 0.000105`
View SolutionIf the mean and variance of a binomial distribution on are 9 and 6
i. i.. Find the distribution.
ii. Find P(`X ge 2`)
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter PROBABILITY of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12
All Exercises from NEW JOYTHI PUBLICATION Class 12 MATHS PROBABILITY
- ADDITIONAL QUESTIONS FOR PRACTICE 13.1
- ADDITIONAL QUESTIONS FOR PRACTICE 13.2
- ADDITIONAL QUESTIONS FOR PRACTICE 13.3
- ADDITIONAL QUESTIONS FOR PRACTICE 13.4
- ADDITIONAL QUESTIONS FOR PRACTICE 13.5
- CONTINUOUS EVALUATION (ASSIGNMENT)
- CONTINUOUS EVALUATION (LAB WORK)
- EXAMPLES
- EXERCISE
- OBJECTIVE TYPE QUESTIONS AND SOLUTIONS
- QUESTIONS FROM COMPETITIVE EXAMS
- SOLUTIONS TO NCERT MISCELLANEOUS EXERCISE
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.1
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.2
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.3
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.4
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.5
- SOLVED EXAMPLES
- UNIT TEST