Complete Solutions to EXAMPLES of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| NEW JOYTHI PUBLICATION | EXAMPLES |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
Three distinguishable fair coins are tossed once or A coin is tossed three times. Write the sample space.
View SolutionConsider the random experiment of rolling two dice. List the sample space.
View SolutionA coin is tossed and then a die is thrown. Describe the sample space.
View SolutionIn each of the following experiments specify appropriate sample space
i. A boy has a 1 rupee coin, a 2 rupee coin and a 5 rupee coin in his pocket. He takes out two coins out of his pocket, one after the other.
ii. A person is noting down the number of accidents along a busy highway during a year.
View SolutionConsider the experiment in which a coin is tossed repeatedly until a tail comes up. Describe the sample space.
View Solution2 boys and 2 girls are in Room X, and 1 boy and 3 girls in Room Y. Specify the sample space for the experiment in which a room is selected and then a person.
View SolutionAn experiment consists of tossing a coin and then throwing it second time if a head occurs. If a tail occurs on the first toss, then a die is rolled once. Find the sample space.
View SolutionSuppose 3 bulbs are selected at random from a lot. Each bulb is tested and classified as defective (D) or non-defective (N). Write the sample space of this experiment.
View SolutionA die is thrown repeatedly until a six comes up. What is the sample space for this experiment?
View SolutionAn experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events:
A : the sum is greater than 8,
B : 2 occurs on either die
C : the sum is atleast 7 and a multiple of 3.
Which pairs of these events are mutually exclusive?
View SolutionTwo dice are thrown. The events A, B and C are as follows:
A: getting an even number on the first die.
B: getting an odd number on the first die.
C: getting the sum of the numbers on the dice `le 5`, state true or false: (give reason for your answer)
i. A and B are mutually exclusive
ii. A and B are mutually exclusive and exhaustive
iii A= B'
iv. A and C are mutually exclusive
v. A and B' are mutually exclusive.
vi. A', B', C are mutually exclusive and exhaustive.
View SolutionA die is rolled. Let E be the event "die shows 4" and F be the event "die shows even number". Are E and F mutually exclusive?
View SolutionThree coins are tossed once. Let A denote the event 'three heads show", B denote the event "two heads and one tail show", C denote the event" three tails show and D denote the event 'a head shows on the first coin". Which events are (i) mutually exclusive? (ii) simple? (iii) compound?
View SolutionA coin is tossed 1000 times in which head occurs 450 times and tail occurs in 550 times. Find the probability of each event.
View SolutionFind the probability of getting head when a coin is tossed once.
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space `S = {omega_(1), omega_(2), omega_(3), omega_(4), omega_(5), omega_(6), omega_(7)}` ?
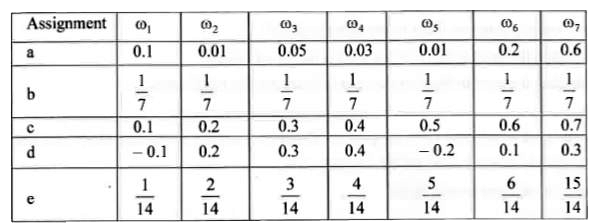
View SolutionA coin is tossed twice, what is the probability that atleast one tail occurs?
View SolutionA card is selected from a pack of 52 cards.
a. How many points are there in the sample space?
b. Calculate the probability that the card is an ace of spades.
c. Calculate the probability that the card is (i) an ace (ii) black card.
View SolutionA bag contains 9 balls of which 4 are red, 3 are white and 2 are green. If a ball is drawn at random, then
i. calculate the probability that it is not white.
ii. it is either white or green.
View SolutionA die is thrown, find the probability of following events:
i. A prime number will appear
ii. A number greater than or equal to 3 will appear
iii. A number less than or equal to one will appear
iv. A number more than 6 will appear
v. A number less than 6 will appear
View SolutionA committee of two persons is selected from two men and three women. What is the probability that the committee will have
i. no man ii. one man only iii. two men
View SolutionA bag contains 5 white, 6 black and 6 yellow balls. 3 balls are drawn at random. Find the probability that of the drawn balls
i. All are black.
ii. Exactly 2 yellow balls are present
iii . Atleast 2 yellow balls are present
View SolutionA bag contains 3 white, 4 black and 2 yellow balls. 2 balls are drawn at random.
i. Find the probability that the two balls drawn are of the same colour.
ii. Find the probability that none of the balls drawn are yellow in colour.
View SolutionA box contains 6 red, 5 blue and 4 green balls. 3 balls are drawn from the box. Find the probability that
i. all are blue
ii. all balls are either red or blue.
iïi. atleast one green ball.
View SolutionThree coins are tossed once. Find the probability of getting
i. 3 heads ii. 2 heads iii. atleast 2 heads
iv. atmost 2 heads V. no head vi. 3 tails
vii. exactly two tails viii. no tail ix. atmost two tails
View SolutionGiven `P(A)= (3)/(5)` and `P(B) =(1)/(5)` Find P(A or B), if A and B are mutually exclusive events.
View SolutionIf `(2)/(11)` is the probability of an event, what is the probability of the event ‘not A'.
View SolutionOne card is drawn from a well shuffled deck of 52 cards. If each outcome is equally likely, calculate the probability that the card will be
i. a diamond
ii. not a diamond
View SolutionIf P(A) = 0.5, P(B) = 0.2, then find P(A U B)' (Given that A and B are mutually exclusive).
View SolutionIf A and B are two events of a random experiment such that `P(A) = (1)/(4), P(B) = (1)/(2)P(A and B)=(1)/(8)` then find i. P(A or B) ii. P (not A and not B).
iii. P(A and not B), P(not A and B)
View SolutionIf A and B are events such that `P(A)=(1)/(5), P(B) =(1)/(3)` and `"P(A and B)"=(1)/(15)`.
i. Find P(A') and P(B'). ii. Find P(A or B)
iii. Find P(A and not B).
View SolutionA and B are two events such that P(A) = 0.5, P(B) = 0.6 and `P(A cap B) = 0.3`.
a. Find `P(A cup B)`. b. Find P(A - B). c. Verify that `P(A cup B)=1-P(A')P(B')`.
View SolutionA bag contains 9 discs of which 4 are red, 3 are blue and 2 are yellow. The discs are similar in shape and size. A disc is drawn at random from the bag. Calculate the probability that it will be (i) red, (ii) yellow, (iii) blue, (iv) not blue, (v) either red or yellow.
View SolutionTwo students A and B, appeared in an examination. The probability that A passes the examination is 0.25 and that B passes is 0.45. Also the probability that both will pass is 0.1. Find the probability that (i) both will not pass (ii) only one of them will pass.
View SolutionTwo students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that
a. Both Anil and Ashima will not qualify the examination.
b. Atleast one of them will not qualify the examination and
c. Only one of them will qualify the examination.
View SolutionFind the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards, it contains (i) all Kings (ii) 3 Kings (iii) atleast 3 Kings.
View SolutionIn a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that
i. The student opted for NCC or NSS.
ii. The student has opted neither NCC nor NSS.
iii. The student has opted NSS but not NCC.
iv. The probability that the student has opted for exactly one of NCC or NSS.
View SolutionA fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12.
View SolutionThere are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
View SolutionIn a lottery, a person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game?
View SolutionCheck whether the following probabilities P(A) and P(B) are consistently defined.
i. P(A) = 0.5, P(B) = 0.7, `P(A cap B) = 0.6`
ii. P(A) = 0.5, P(B) = 0.4, `P(A cup B) = 0.8`
View SolutionEvents E and F are such that P(not E or not F) = 0.25, State whether E and F are mutually exclusive.
View SolutionA and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16. Determine
(i) P(not A), (ii) P(not B) (iii) P(A or B) (iv) `P(A cup B)`
View SolutionIn Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
View SolutionIn an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleast one of them is 0.95. What is the probability of passing both?
View SolutionThe probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?
View SolutionA box contains 10 red marbles, 20 blue marbles and 30 green marbles. 5 marbles are drawn from the box, what is the probability that
(i) all will be blue? (ii) atleast one will be green?
View Solution4 cards are drawn from a well - shuffled deck of 52 cards. What is the probability of obtaining 3 diamonds and one spade?
View SolutionA die has two faces each with number '1', three faces each with number '2' and one face with number '3'. If die is rolled once, determine
i. P(2) ii. P(1 or 3) iii. P(not 3)
View SolutionIn a certain lottery 10,000 tickets are sold and ten equal prizes are awarded. What is the probability of not getting a prize if you buy (a) one ticket (b) two tickets (c) 10 tickets?
View SolutionOut of 100 students, two sections of 40 and 60 are formed. If you and your friend are among the 100 students, what is the probability that
a. you both enter the same section? b. you both enter the different sections?
View SolutionThree letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in its proper envelope.
View SolutionA and B are two events such that P(A) = 0.54, P(B) = 0.69 and `P(A cap B) = 0.35`. Find i. `P(A cup B)` ii. `P(A' cap B')` iii. `P(A cap B')` iv. `P(B cap A')`
View SolutionFrom the employees of a company, 5 persons are selected to represent them in the managing committee of the company, Particulars of five persons are as follows:
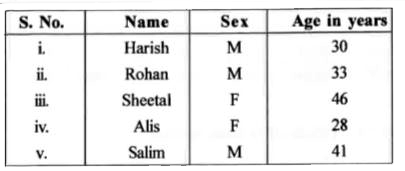
A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will be either male or over 35 years?
View SolutionIf 4-digit numbers greater than 5,000 are randomly formed from the digits 0, 1, 3, 5, and 7, what is the probability of forming a number divisible by 5 when,
(i) the digits are repeated? (ii) the repetition of digits is not allowed?
View SolutionThe number lock of a suitcase has 4 wheels, each labelled with ten digits i.e., from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the right sequence to open the suitcase?
View SolutionA letter is chosen at random from the word 'ASSASSINATION'. Find the probability that letter is (i) a vowel (ii) a consonant.
View Solution
EXAMPLES questions and complete solutions for chapter PROBABILITY of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12
All Exercises from NEW JOYTHI PUBLICATION Class 12 MATHS PROBABILITY
- ADDITIONAL QUESTIONS FOR PRACTICE 13.1
- ADDITIONAL QUESTIONS FOR PRACTICE 13.2
- ADDITIONAL QUESTIONS FOR PRACTICE 13.3
- ADDITIONAL QUESTIONS FOR PRACTICE 13.4
- ADDITIONAL QUESTIONS FOR PRACTICE 13.5
- CONTINUOUS EVALUATION (ASSIGNMENT)
- CONTINUOUS EVALUATION (LAB WORK)
- EXAMPLES
- EXERCISE
- OBJECTIVE TYPE QUESTIONS AND SOLUTIONS
- QUESTIONS FROM COMPETITIVE EXAMS
- SOLUTIONS TO NCERT MISCELLANEOUS EXERCISE
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.1
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.2
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.3
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.4
- SOLUTIONS TO NCERT TEXT BOOK EXERCISE 13.5
- SOLVED EXAMPLES
- UNIT TEST