Complete Solutions to EXAMPLES of chapter APPLICATION OF INTEGRALS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATION OF INTEGRALS |
| NEW JOYTHI PUBLICATION | EXAMPLES |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Find the area of the circle `x^(2) + y^(2) = a^(2)` using integration.
View SolutionConsider the curve`(x^(2))/(16) + (y^(2))/(9) = 1`
(i)Find the points of intersection with x- axis.
(ii) Find the area of the region bounded by the curve.
View Solution(1) Draw the rough sketch of the ellipse `(x^(2))/(a^(2)) + (y^(2))/(b^(2)) = 1`.
Find the area enclosed by the ellipse `(x^(2))/(a^(2)) + (y^(2))/(b^(2)) = 1`.
View SolutionFind the area of the region bounded by the curve `y = x^(2)` and the line y = 4.
View SolutionConsider the parabola `y^(2) = 4ax`
(i) Write the equation of the rectum and obtain the x co-ordinates of the point of intersection of latus rectum and the parabola.
(ii) Find the area of the parabola bounded by the latus rectum.
View Solution(i)
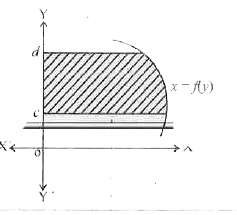
Area of the shaded portion in the figure is equal to
(a) `int_(d)^(c)f(x)dx` (b) `int_(c)^(d) f(x) dx`
(c)`int_(d)^(c)f(y)dy` (d) `int_(c)^(d)f(y)dy`
(ii) Consider the curve `y = x^(2), x = 0, y = 1, y = 4`.Draw a rough sketch and shade the region bounded by the these curves. Find the area of the shaded region.
View SolutionFind the area bounded by the ellipse `(x^(2))/(a^(2)) + (y^(2))/(b^(2)) = 1` and the lines x = 0 and x = ae where`b^(2) = a^(2)(1 - e^(2))` and `e lt 1`.
View SolutionFind the area of the region bounded by the parabola `y = x^(2) + 2` , x-axis, x = 0 and x = 3.
View SolutionFind the area of the region bounded by the curve `y = |x|` and the x- axis between x = - 4 and x - 2`.
View SolutionFind the area of the region bounded by x-axis, the curve `y=|cosx|`, the lines x=0 and `x=pi`.
View SolutionFind the area bounded by the curvey = sinx between x = 0 and `x = 2pi`.
View Solution(i) Find the point at which the circle `x^(2) + y^(2) = 32` intersects the positive x-axis.
(ii) Shade the region in the first quadrant enclosed by the x-axis, the line y = x and the circle `x^(2) + y^(2) = 32`.
(iii) Using integration, find the area of the shaded region.
View SolutionConsider the circle `x^(2) + y^(2) = 16` and the straight line `y = sqrt3x` as shown in the figure.
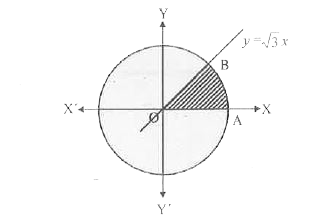
(i)Find the points A and B as shown in the figure.
(ii) Find the area of the shaded region in the figure using definite integral.
View SolutionConsider the curve `y = x^(2)` and the straight line `y = 2x + 3`.
(i) Find the points of intersection of the given curve and the straight line.
(ii) Find the area of the region bounded by the given curve and the straight line.
View SolutionFind the area bounded by the curve `x^(2) = 4y` and the line `x = 4y -2`.
View Solution(i) Find the points of intersection of the parabola `y ^(2) = 8x` and the line `y = 2x`.
(ii) Find, using integration, the area enclosed between the line and the parabola.
View SolutionConsider the functions, `f(x) = |x| - 1` and `g(x) = 1 - |x|` (a) Sketch their graphs and shade the closed region between them. (b) Find the area of their shaded region.
View SolutionUsing integration, find the area of the region bounded by the triangle whose vertices are (0, 1), (2,2) and (3, 1).
View Solution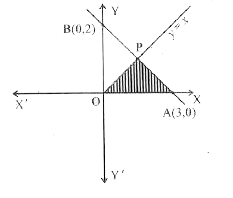
Using the above figure
(a).Find the equation of AB.
(b) Find the point P.
(c) Find the area of the shaded region by integration.
View SolutionUsing the method of integration find the area of the region bounded by lines :
`2x + y = 4, 3x - 2y = 6` and `x - 3y + 5 = 0`.
View SolutionIn the figure given below, AOBA is the part of the ellipse `9x^(2) + y^(2) = 36` in the first quadrant such that OA = 2 and OB = 6. Find the area between arc AB and the chord AB
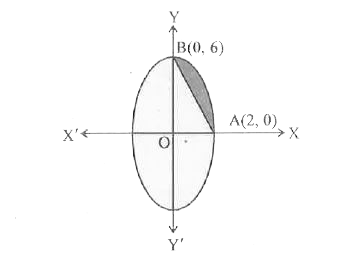
View SolutionConsider the curves `y^(2) = x` and `x^(2) = y`.
(i) Find the points of intersection of these two curves.
(ii) Find the area between these two curves.
View SolutionConsider the curves `y = x^(2)` and `y^(2) = 8x`.
(i) Find the points of intersection of the given two curves.
(ii) Find the area of the region enclosed by the given two curves
View SolutionFind the area of the region bounded by the parabola `y = x^(2)` and `y = |x|`.
View SolutionFind the area lying above x-axis and included between the circle `x^(2) + y^(2) = 8x` and inside the parabola `y^(2) = 4x`.
View SolutionFind the area enclosed between the circles `x^(2) + y^(2) = 4` and `(x - 2)^(2) + y^(2) = 4`.
View SolutionProve that the curves `y^(2) = 4x` and `x^(2) = 4y` divide the area of the square bounded by x = 0, x = 4 and y = 0 into three equal parts.
View SolutionLet us find the area of the region bounded by the curve ` y^(2) = 8x at x =1 , x =3 ` and the x- axis in the first quadrant .
View Solution
EXAMPLES questions and complete solutions for chapter APPLICATION OF INTEGRALS of NEW JYOTHI MATHS (TAMIL ENGLISH) of Class 12
All Exercises from NEW JOYTHI PUBLICATION Class 12 MATHS APPLICATION OF INTEGRALS
- ADDITIONAL QUESTIONS FOR PRACTICE 8.1
- ADDITIONAL QUESTIONS FOR PRACTICE 8.2
- CONTINUOUS EVALUATION (ASSIGNMENT )
- CONTINUOUS EVALUATION (LAB Work )
- CONTINUOUS EVALUATION (PROJECT )
- EXAMPLES
- NCERT TEXT BOOK EXERCISE 8.1
- NCERT TEXT BOOK EXERCISE 8.2
- OBJECTIVE TYPE QUESTIONS AND SOLUTIONS
- SOLUTIONS TO NCERT MISCELLANEOUS EXERCISE
- UNIT TEST