(i)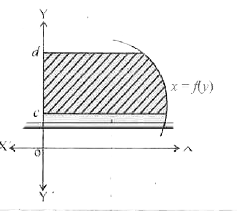
Area of the shaded portion in the figure is equal to
(a) ∫cdf(x)dx (b) ∫dcf(x)dx
(c)∫cdf(y)dy (d) ∫dcf(y)dy
(ii) Consider the curve y=x2,x=0,y=1,y=4.Draw a rough sketch and shade the region bounded by the these curves. Find the area of the shaded region.Solution in Tamil
The correct Answer is:(i)d. ∫dcf(y)dy
ii.283sq.units
Step by step video, text & image solution for (i) Area of the shaded portion in the figure is equal to (a) int_(d)^(c)f(x)dx (b) int_(c)^(d) f(x) dx (c)int_(d)^(c)f(y)dy (d) int_(c)^(d)f(y)dy (ii) Consider the curve y = x^(2), x = 0, y = 1, y = 4.Draw a rough sketch and shade the region bounded by the these curves. Find the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF INTEGRALSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - APPLICATION OF INTEGRALSEXERCISE - NCERT TEXT BOOK EXERCISE 8.1
13 Videos
- APPLICATION OF INTEGRALSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - APPLICATION OF INTEGRALSEXERCISE - NCERT TEXT BOOK EXERCISE 8.2
7 Videos
- BINOMIAL THEOREMBOOK - NEW JOYTHI PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS
51 Videos
Similar Questions
Find the area of the region bounded by the curve y2=x and the lines x = 1, x = 4 and the x -axis.
View SolutionFind the area of the circle4x2+4y2=9 which is interior of the parabola x2=4y.
View SolutionIf T, denotes the rth term in the expansion of [x+1x]23, then
View SolutionWhich of the following is incorrect? ∫b+ca+cf(x)dx=∫baf(x+c)dx ∫bcacf(x)dx=c∫baf(cx)dx ∫a−af(x)dx=12∫a−a(f(x)+f(−x)dx None of these
View SolutionP(alpha,f(alpha)) and Q(beta,f(beta)) are ends of an arc in the first quadrant.The area bounded by the arc,ordinates through P and Q, and the x -axis is (A) int_(f(alpha))^(f(beta))f^(-1)(y)dy(B)int_(alpha)^( beta)f^(-1)(y)dy(C)int_(alpha)^( beta)f(x)dx(D)int_(f(alpha))^(f(beta))f(x)dx
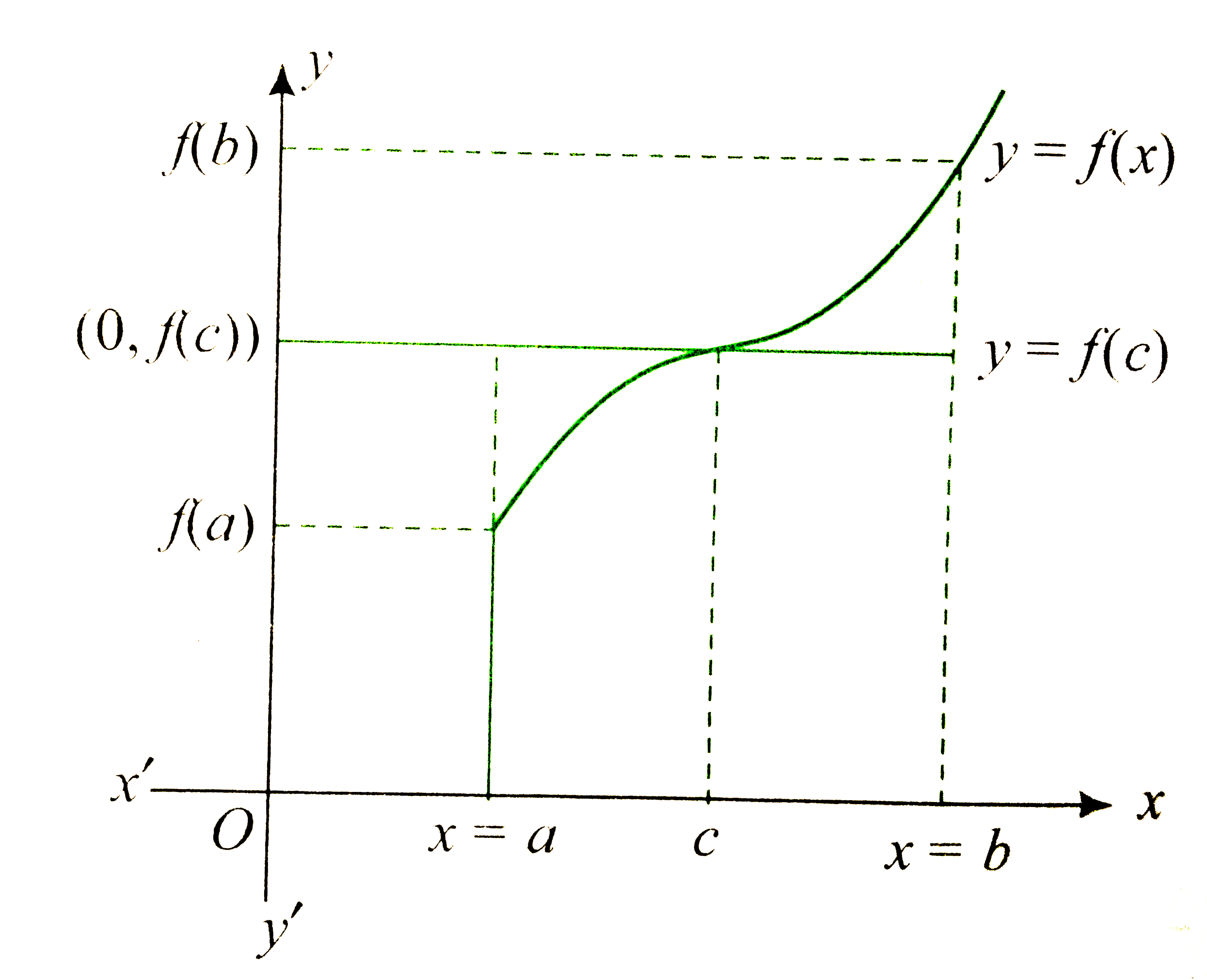
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is
View Solution∫badx=∫caf(x)dx+∫caf(x)dx,a<c<b.
View SolutionIf ∫10f(x)dx=1 and ∫21f(y)dy=2, then ∫20f(z)dz=
View SolutionIf ∫30f(x)dx=1 and ∫40f(y)dy=2, then ∫43f(z)dz=
View SolutionIf ∫b−c0f(x+c)dx=a∫cbf(x)dx, then a =
View SolutionIf X= {a,b,c,d} , Y = {f , b,d,g} , find:
(i) X-Y
(ii) Y-X.
View Solution(i) Draw a rough sketch of the curve y2=x and shade the region bounded by the line x = 1 and the curve.
(ii) Using integration find the area of the shaded region.
View SolutionIf ∫b−c0f(x+c)dx=k∫cbf(x)dx then k=
View SolutionMatch the following
List - 1List - III) ∫1−1x|x|dxa) π2II) ∫π20(1+log(4+3sinx4+3cosx))dxb) ∫π20f(x)dxIII) ∫a0f(x)dxc) ∫a0[f(x)+f(−x)]dxIV) ∫a−af(x)dxd) 0e) ∫a0f(a−x)dx
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b))isminiμmwhen
c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is
View Solution

