Complete Solutions to प्रश्नावली (स्तर 2 ) of chapter स्थिर वैद्युतिकी of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | स्थिर वैद्युतिकी |
| ARIHANT HINDI | प्रश्नावली (स्तर 2 ) |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
दो बराबर आवेशित छोटी गेंद एकड़-दूसरे से एक निश्चित दूरी पर स्थिर है, ये एक बल F अनुभव करती है। एक छोटी अनावेशित गेंद को इनमे से एक गेंद से स्पर्श कराकर मध्य बिन्दु पर रख देते है। इस गेंद पर लगने वाला बल है।
View Solutionएकसमान रूप से आवेशित वलय जिसका आवेश q तथा त्रिज्या R है, की महत्तम वैद्युत क्षेत्र की तीव्रता होगी
View Solutionआवेश `2q,-q` तथा `-q` एक समबाहु त्रिभुज के शीर्षो पर स्थित है। E तथा V के मान त्रिभुज के केन्द्रक पर होंगे
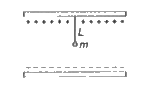
View Solutionयदि एक धनात्मक आवेशित पेण्डुलम एकसमान वैद्युत क्षेत्र में चित्रानुसार दोलन करता है, इसके आवर्तकाल की तुलना जब यह अनावेशित है तब के आवर्तकाल से करे तो इसका आवर्तकाल होगा । ।

View Solutionदो बराबर आवेश एक भुजा वाले समबाहु त्रिभुज (ABC) के शीर्षो A तथा B पर रखे है, बिन्दु C परावैद्युत क्षेत्र की तीव्रता है।
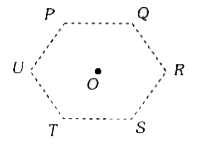
View Solutionएक समषट्भुज के कोनों पर समान परिमाण के तीन धन और तीन ऋण आवेश रखने पर इसके केन्द्र O पर उत्पन्न विद्युत क्षेत्र उस स्थिति का दुगना होगा, जिसमें सिर्फ R पर समान परिमाण का एक आवेश रखा जाये | P,Q,R, S,T, एवं U पर आवेशों का कौन सा समायोजन उचित होगा
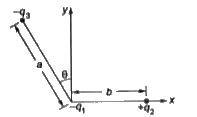
View Solutionतीन आवेश `-q_(1),+q_(2)` तथा `-q_(3)` चित्रानुसार रहे है। `-q_(1)` पर बल का x घटक अनुक्रमानुपाती है।
View Solutionएक छोटे वैद्युत द्विध्रुव की अक्ष पर लम्बवत द्विभाजक पर r दूरी पर वैद्युत क्षेत्र `E_(1)` तथा `2r` दूरी पर `E_(2)` है, तब
View SolutionR त्रिज्या के वृत्त के केन्द्र पर `Q_(2)` आवेश रखा है, इसके चारो ओर `q_(1)` आवेश को घुमाने में किया गया कार्य है।
View Solutionएक खोखले धात्विक गोले की त्रिज्या r है। यदि इसके पृष्ठ तथा पृष्ठ से 3r दूरी पर विभवांतर V है, तब 3r दूरी पर वैद्युत क्षेत्र की तीव्रता है
View Solutionxy-समतल में बिन्दु `(x,y)` पर वैद्युत विभव दिया गया है, `V=-Kxy` वैद्युत क्षेत्र की तीव्रता में मूल बिन्दु से दूरी r के साथ परिवर्तन इस प्रकार होता है।
View Solutionयदि किसी बन्द पृष्ठ से प्रवेशित तथा निर्गत वैद्युत फ्लक्स क्रमशः `phi_(1)` व `phi_(2)` हो, तो पृष्ठ के अन्दर विद्युत आवेश होगा
View Solutionदो बिन्दु आवेश `+q` तथा `-q(x,y)` समतल के दो बिंदुओं क्रमशः `(-d,0)` तथा `(d,0)` पर रखे है, तब
View Solutionनिम्न चित्रों में कौन-सा चित्र यह दर्शाता है कि एक वैद्युत द्विध्रुव की स्थितिज ऊर्जा महत्तम है?
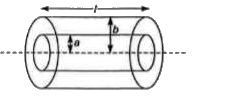
View Solutionएक आवेशित बेलनाकार संधारित्र के पूरे क्षेत्र में वैद्युत क्षेत्र E का परिमाण है।
View Solutionएक धनात्मक बिन्दु आवेश q एक बिन्दु B से बिन्दु A तक O पर रखे `+Q` बिन्दु आवेश के वैद्युत क्षेत्र में आता है। यदि निर्वात की वैद्युतशीलता `epsilon_(0)` है तो इस प्रक्रम में किया गया कार्य है (जहाँ, `a=OA` तथा `b=OB`)
View Solutionचित्र में दिखाई गई तीन बड़ी प्लेटो का आवेश पृष्ठ घनत्व एकसमान है। बिन्दु P पर वैद्युत क्षेत्र है।

View Solutionएक इलेक्ट्रॉन को `100eV` से एक `2xx10^(-6)` कूलॉम/मी`.^(-2)` आवेश पृष्ठ घनत्व वाली बड़ी चादर की ओर `100eV` से प्रक्षेपित किया जाता है। वह दूरी जहाँ से इलेक्ट्रॉन को प्रेक्षपित करने पर वह प्लेट से तकरायेगा
View Solutionतीन समकेन्द्रीय वलयो पर तीन आवेश आन्तरिक वालय पर `+Q` आवेश बीच वाली वलय पर `-2Q` आवेश तथा बाह्य वलय पर `-5Q` आवेश है।
View Solutionएकसमान वैद्युत क्षेत्र x-अक्ष की दिशा में लगा है। यदि A मूल बिन्दु है तथा B, x-अक्ष पर `x=+1` सेमी दूरी पर स्थित है तथा C, y-अक्ष पर `y=+1` सेमी दूरी पर स्थित बिन्दु है। तब A, B तथा C पर विभव निम्न सम्बन्ध को संतुष्ट करता है। तो सही विकल्प होगा
View Solutionएक आवेशित बस्तु से बद्ध वैद्युत फ्लक्स `phi` है। अब वस्तु को एक धात्विक कन्टेनर में रखते है। कन्टेनर से बद्ध बन्द विद्युत फ्लक्स होगा
View Solutionमाना आवेश विन्यास तथा एक गोलाकार गासियन पृष्ठ चित्र में दिखाया गया है। जब गोलाकार पृष्ठ के ऊपर वैद्युत फ्लक्स मापते है, तो वैद्युत क्षेत्र होता है।

View Solutionचार बराबर आवेश प्रत्येक `-Q` एक वर्ग के चारो कोनो पर रखे है तथा आवेश q उसके केन्द्र पर रखा है। यदि निकाय साम्य में है, तो q का मान है।
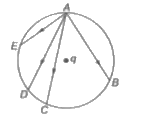
View Solutionएक बिन्दु आवेश q के वैद्युत क्षेत्र में एक निश्चित बिन्दु आवेश को A से B, C, D तथा E तक चित्रानुसार रखा जाता है। किया गया कार्य है।
View Solutionदो गोले जिनकी त्रिज्याएँ `R_(1)` तथा `R_(2)` है, एक पतले तार से जुड़े है तथा उनका विभव V बढ़ता है। यदि `sigma_(1)` तथा `sigma_(2)`, इन दोनों गोलों के क्रमशः आवेश पृष्ठ घनत्व है, तब अनुपात `(sigma_(2))/(sigma_(1))` है।
View Solutionएक अचालकीय वलय जिसकी त्रिज्या 0.5 मी है, इसका कुल आवेश `1.11xx10^(-10)` कूलॉम है इसकी परिधि आसमान रूप से वितरित है। यह पूरे पृष्ठ पर वैद्युत क्षेत्र उत्पन्न करता है, रेखीय समाकलन
`oint_(l=oo)^(l=0)-E.dl` (`l=0`, वलय का केन्द्र है) का मान है।
View Solutionएक ठोस चालकीय गोले का आवेश Q है इसके चारो ओर एक सकेंद्रीय खोखली गोलाकार चालकीय वलय है। माना ठोस गोले के पृष्ठ तथा वलय के पृष्ठों के बीच विभवांतर V है। यदि वलय को अब `-3Q` आवेश दिया जाता है, तो उन पृष्ठों के बीच विभवांतर है।
View Solutionb मोटाई की एक कॉपर स्लैब चित्रानुसार एक समान्तर प्लेट संधारित्र की प्लेटो के बीच रखी है। प्लेटो के बीच की दूरी d है। यदि `b=d//2`, तब स्लैब रखने से पहले संधारित्र की धारित्र तथा बाद में संधारित्र की धारिता का अनुपात होगा
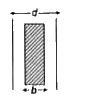
View Solutionचित्र में दिय गए परिपथ के लिए, निम्नलिखित में से कौन-सा कथन सत्य है?
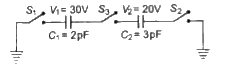
View Solutionदो एकसमान धात्विक प्लेटों पर क्रमशः `Q_(1)` तथा `Q_(2)(ltQ_(1))` आवेश है। यदि इनसे C धारिता वाला समान्तर प्लेट संधारित्र बनाया जाता है, तो इनके बीच विभवांतर है।
View Solutionदो एकसमान संधारित्रों की धारिता C है। एक को विभव `V_(1)` द्वारा आवेशित किया जाता है जबकि दूसरे को विभव `V_(2)` द्वारा आवेशित किया जाता है। संधारित्रों के ऋणात्मक सिरे एक-दूसरे से जुड़े है। जब इनके धनात्मक सिरों को जोड़ा जाता है तो निकाय की ऊर्जा में कमी है।
View Solutionसंधारित्र जिनमे प्रत्येक की धारिता `2muF` है, इस प्रकार जोड़े जाते है कि परिणामी धारिता `(10)/(11)muF` प्राप्त हो चित्र में दिखाए निम्न संयोजनों में से कौन-सा इस परिणाम को दिखाता है?
View Solutionतीन धात्विक प्लेटों A, B तथा C जिनके पृष्ठ क्षेत्रफल तथा बीच की दूरी d बराबर है, चित्र में दिखाए गए है। जब प्लेटें पूर्ण आवेशित हो जाती है, तब इस व्यवस्था में संचित ऊर्जा है।

View Solutionएक समान्तर प्लेट संधारित्र जिसका क्षेत्रफल A प्लेटों के बीच की दूरी d तथा धारिता C है। चित्रानुसार तीन परावैद्युत पदार्थो जिनके परावैद्युतांक क्रमशः `K_(1),K_(2)` तथा `K_(3)` से भरा है, यदि एकल परावैद्युत पदार्थ का प्रयोग करने पर भी संधारित्र की धारिता C ही रहती है तब परावैद्युतांक K है।
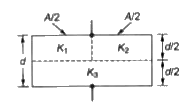
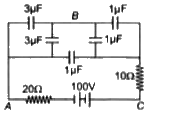
View Solutionदिय गए परिपथ में `C_(1)=C_(2)=C_(3)=30pF` तथा `C_(4)=120pF` है। यदि संधारित्रों का संयोजन `140V DC` से आवेशित किया जाता है, तब चार संधारित्रों में विभवांतर क्रमशः होंगे
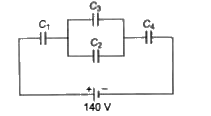
View Solutionचित्र में दिखाए गए संधारित्रों के संयोजन में प्रत्येक `9muF` का है, तब A तथा B के बीच तुल्य धारिता है।
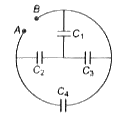
View Solutionदो गोलाकार संधारित्र A तथा B जिनकी त्रिज्याएँ 1 मिमी तथा 2 मिमी है इनके बीच की दूरी 5 सेमी है तथा ये एकसमान रूप से आवेशित है। यदि गोले एक धात्विक तार द्वारा जुड़े हुए है, तब साम्य अवस्था में A तथा B के पृष्ठों के वैद्युत क्षेत्रो का अनुपात है।
View Solutionतीन एकसमान संधारित्रों जिनमे प्रत्येक की धारिता C है चित्र में दिखाया गया है। बिंदुओं A तथा B के बीच तुल्य धारिता है।
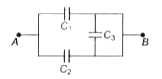
View Solutionनिर्वात में किसी बिन्दु `x,y,z` (सभी मीटर में) पर वैद्युत विभव V सूत्र `V=4x^(2)` वोल्ट द्वारा दिया गया है। बिन्दु (1 मी, 0, 2 मी) पर वोल्ट/मी में वैद्युत क्षेत्र है।
View Solutionचित्र में दिय गए परिपथ में अपरिवर्ती धारा है संधारित्र C में विभव पतन है
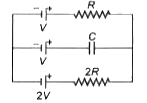
View Solutionदो स्थिर कणो A तथा B के आवेश क्रमशः `8xx10^(-6)` कूलॉम तथा `-2xx10^(-6)` कूलॉम है, इनके बीच की दूरी 20 सेमी है। तीसरा आवेशित कण कहाँ रखा जाए कि वह कोई बल अनुभव न करे?
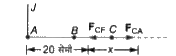
View Solutionएक वैद्युत द्विध्रुव जिसका आघूर्ण `4xx10^(-9)` कूलॉम-मी है, यह `5xx10^(4)` न्यूटन/कूलॉम परिमाण वाले एकसमान वैद्युत क्षेत्र कि दिशा से `30^(@)` का कोण बनाते हुए रखा गया है। द्विध्रुव पर लगने वाले बलाघूर्ण का परिमाण है।
View Solutionचित्र में वैद्युत क्षेत्र दिखाया गया है बाई दिशा में वैद्युत बल रेखाओं के बीच की दूरी दाई ओर की उनके बीच की दूरी की दोगुनी है। यदि बिन्दु A पर क्षेत्र का परिमाण 40 न्यूटन/कूलॉम है तो बिन्दु A पर रखे प्रोटॉन पर लगने वाला बल है।
View Solutionदो अचालकीय पदार्थ के गोलों की धारिता में `3muF` तथा `5muF` है, इन्हे क्रमशः 300 वोल्ट तथा 500 वोल्ट विभव द्वारा आवेशित किया जाता है। जब इन्हे एक तार द्वारा जोड़ा जाता है, तो ऊर्जा हानि है।
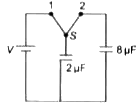
View Solutionएक `2muF` धारिता वाला संधारित्र चित्रानुसार आवेशित किया जाता है। जब कुंजी S, स्थिति 2 पर विस्थापित हो जाती है तब संचित ऊर्जा में प्रतिशत हानि है।
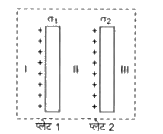
View Solutionदो समान्तर समतल प्लेटों 1 तथा 2 के एकसमान आवेश घनत्व `sigma_(1)` व `sigma_(2)` है जो चित्र में दिखाए गए है। बिन्दुकित किय गए क्षेत्र III में परिणामी वैद्युत क्षेत्र होगा ।
`(sigma_(1)gtsigma_(2))`
View Solutionएक `4muF` का संधारित्र तथा एक `2.5Omega` का प्रतिरोधक एक `12V` की बैटरी के साथ श्रेणी क्रम में जुड़े है। कितने समय बाद संधारित्र में विभवांतर, प्रतिरोधक में विभवांतर का तीन गुना हो जायेगा? दिया है `log_(e)(2)=0.693`
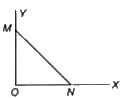
View Solutionचित्रानुसार `+q` बिन्दु आवेश मूल बिन्दु O पर रखा है। एक अन्य बिन्दु आवेश `-Q` को बिन्दु `A(0,a)` से बिन्दु `B(a,0)` तक सरल रेखीय पथ AB द्वारा ले जाने में किया गया कार्य है।
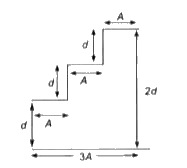
View Solutionचित्र में दिखाए गए निकाय की तुल्य धारिता है (A एक प्लेट का अनुप्रस्थ परिच्छेद क्षेत्रफल है)
View Solutionएक अर्द्धवृत्ताकार वृत्तखण्ड की त्रिज्या a है, यह एकसमान रूप से आवेशित `lambda` है इसका रेखीय आवेश घनत्व `lambda` है। इसके केन्द्र पर वैद्युत क्षेत्र होगा ।
View Solutionएक छोटे गोले का आवेश q है, यह समान्तर प्लेटों के बीच l लम्बाई की स्ट्रियर द्वारा रखा है। दोलन का आवर्तकाल 10 है। जब समान्तर प्लेटों को आवेशित किया जाता है, आवर्तकाल में T का परिवर्तन हो जाता है। अनुपात `(T)/(10)` है।
View Solutionदो धनात्मक आयन जिनमे प्रत्येक का आवेश q है, एक दूरी द्वारा एक दूसरे से अलग है। यदि F आयनों के बीच प्रतिकर्षण बल है, प्रत्येक आयन द्वारा उत्सर्जित इलेक्ट्रॉनों की संख्या है, जबकि इलेक्ट्रॉन का आवेश e है।
View Solutionअनन्त आवेश जिनमे प्रत्येक `1muC` है, x-अक्ष पर निर्देशांकों `x=1,2,4,8…oo` पर रखे है। यदि एक `1C` का आवेश मूल बिन्दु पर रख दिया जाए तब `1C` आवेश पर कार्यरत नेट बल है
View Solutionदो कण जिनके समान द्रव्यमान m तथा आवेश q है, एक-दूसरे से 16 सेमी की दूरी पर रखे है। वे कोई नेट बल अनुभव नहीं करते है। `(q)/(m)` का मान है।
View Solutionतीन आवेश जिनमे प्रत्येक का परिमाण q एक समबाहु `Delta` के कोनो पर रखे है। इसके केन्द्र पर रखे आवेश पर स्थिर वैद्युत बल है।
View Solutionदो बिन्दु आवेश वायु में एक-दूसरे से r दूरी पर रखे है तथा एक-दूसरे पर F बल लगाते है। जब इन आवेशों को K परावैद्युतांक के माध्यम में एक-दूसरे से r दूरी पर रखा जाता है तो ये एक-दूसरे पर कितना बल आरोपित करते है?
View Solutionपाँच गेंदे क्रमशः 1 से 5 तक अलग-अलग धागो से लटकी हुई है। जोड़े `(1,2),(2,4)` तथा `(4,1)` के मध्य स्थिर वैद्युतिकी आकर्षण, जबकि जोड़ो `(4,5)` के मध्य प्रतिकर्षण होता है, गेंद 1 होगी
View Solutionतीन प्लेटें जिनका उभयनिष्ठ क्षेत्रफल A है, चित्रानुसार जुडी है प्रभावी धारिता होगी
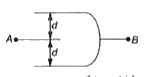
View Solutionएक ठोस धात्विक गोले का आवेश `+3Q` है। इसके चारो ओर एक संकेन्द्रीय धात्विक वलय है, इसका आवेश `-Q` है। ठोस गोले की त्रिज्या a तथा वलय की त्रिज्या `b(bgta)` है। दूरी `R(bltRltb)` पर वैद्युत क्षेत्र है?
View Solutionयदि समकेन्द्रीय खोखले गोलों की त्रिज्या r तथा `R(gtr)` है। Q आवेश इन पर वितरित किया गया है अर्थात इनका आवेश पृष्ठ घनत्व समान है तब इनके उभयनिष्ठ केन्द्र पर विभव है।
View Solutionदो बराबर तथा विपरीत चिन्ह के दो आवेश एक द्विध्रुव के रूप में, इनके बीच की दूरी 2a तथा द्विध्रुव आघूर्ण p है। यदि P द्विध्रुव के केन्द्र से दूरी r पर कोई बिन्दु है तथा द्विध्रुव के केन्द्र से बिन्दु P को मिलाने वाली रेखा इसकी अक्ष के साथ `theta` कोण बनाती है, तब p पर विभव `(rgt2a)` (जहाँ `p=2qa`) दिया गया है।
View Solutionएक बिन्दु आवेश `q,a` भुजा वाले वर्ग के केन्द्र से सीधे ऊपर `a//2` पर रखा है। वर्ग से गुजरने वाला वैद्युत फ्लक्स है।
View Solutionदो एकसमान लम्बे समान्तर तारो के रेखीय आवेश धनत्व क्रमशः `lambda_(1)` तथा `lambda_(2)` है, इन्हे एक-दूसरे से R दूरी पर रखा गया है, किसी एक तार पर प्रति एकांक लम्बाई का बल होगा `(K=(1)/(4piepsilon_(0)))`
View Solutionदो एकसमान पतली वलय जिनमे प्रत्येक की त्रिज्या R मीटर है, दोनों एक दूसरे से R दूरी पर समाक्षीय रूप से रखी है। यदि `Q_(1)` कूलॉम तथा `Q_(2)` कूलॉम आवेश क्रमशः एकसमान रूप से दो वलयो पर फैले हुए है, आवेश q को एक वलय के केन्द्र से दूसरी वलय के केन्द्र तक जाने में किया गया कार्य है।
View Solutionदो बराबर ऋण आवेश `-q` बिंदुओं `(0,a)` तथा `(0,-a)` पर p-अक्ष पर स्थित है। एक धनावेश Q, x-अक्ष के बिन्दु `(2a,0)` से छोड़ा जाता है। आवेश Q होगा
View Solutionनीचे दिय गए चित्र में अपरिवर्ति धारा में बिन्दुओं A तथा B तथा बिन्दुओं B तथा C के बीच विभवान्तर क्रमशः है।
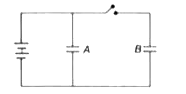
View Solutionनिम्न चित्र में दो सर्वसम संधारित्र एक बैटरी ओर एक बन्द बटन संयोजित किय गए है। अब बटन को विच्छेदित (OFF) करके संधारित्रों कि प्लेटों के मध्य 3 परावैद्युतांक वाला परावैद्युत भरा गया है। दोनों संधारित्रों की कुल स्थैतिक विद्युत ऊर्जा का अनुपात, परावैद्युत भरने के पूर्व और पश्चात होगा
View Solutionएक समान्तर प्लेट संधारित्र C धारिता की बैटरी से जुड़ा है और V विभवांतर से आवेशित है। अन्य 2C धारिता का संधारित्र अन्य बैटरी से जुड़ा है, जो `2V` विभवांतर से आवेशित है। आवेशित करने वाली बैटरी को अब हटा दिया जाता है, और संधारित्रों को अब समान्तर क्रम में इस प्रकार जोड़ दिया जाता है, कि एक संधारित्र क धनात्मक सिरा, दूसरे संधारित्र के ऋणात्मक सिरे से जुड़े हो। इस विन्यास की अन्तिम ऊर्जा है।
View Solutionचित्र में दिखाए अनुसार बहुत से `2muF, 4muF` धारिता के संधारित्रों के संयोग सम्बन्धित कर एक परिमित श्रेणी बनाई जाती है। यह श्रेणी धारिता C के एक संधारित्र द्वारा समाप्त होती है। C का मान क्या होना चाहिए जिससे A और B बिन्दुओं के बीच श्रेणी की समतुल्य धारिता इनके बीच में संयोगो की संख्या पर निर्भर न करे
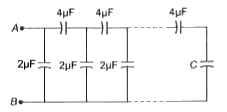
View Solutionएक वैद्युत द्विध्रुव `10^(5)` न्यूटन/कूलॉम तीव्रता वाले वैद्युत क्षेत्र से `60^(@)` का कोण बनाते हुए रखा गया है। यह एक बलाघूर्ण का अनुभव करता है। यदि द्विध्रुव की लम्बाई 2 सेमी है तो द्विध्रुव का आवेश होगा
View Solutionतीन अनन्त विस्तार की आवेशित प्लेटें समान्तर रूप से xy-तल में रखी है, इनके आवेश घनत्व चित्र में दिखाए गए है तब बिन्दु P पर वैद्युत क्षेत्र का मान है

View Solutionदो विपरीत एवं बराबर आवेशों `q=1xx10^(-6)` कूलॉम को 2.0 सेमी दूरी पर रखने से एक द्विध्रुव बनता है। यदि इस द्विध्रुव को `1xx10^(5)` न्यूटन/मी के बाह्य वैद्युत क्षेत्र में रखा जाए तो उस पर लगने वाला अधिकतम बलाघूर्ण और इसे `180^(@)` से घुमाने में किय गए कार्य का मान होगा?
View Solutionदो रोधी आवेशित चालकीय गोले जिनकी त्रिज्याएँ क्रमशः 20 सेमी एवं 15 सेमी है तथा उनके आवेश q बराबर है। ये एक ताम्बे के तार द्वारा जोड़े जाते है फिर ये अलग-अलग किये जाते है, तो
View Solutionचित्रानुसार बिन्दु आवेश q धनात्मक x-अक्ष की दिशा के समान्तर एकसमान विद्युत क्षेत्र में P से S की दिशा में PQRS के अनुदिश गति करता है।
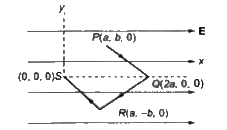
P, Q, R व S के निर्देशांक क्रमशः `(a,b,0),(2a,0,0),(a,-b,0)` व `(0,0,0)` है। क्षेत्र द्वारा उपरोक्त प्रक्रिया में किया गया कार्य है।
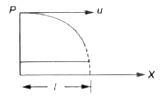
View Solutionएक इलेक्ट्रॉन d दूरी से u वेग से एकसमान आवेश के समान्तर प्रक्षेपित किया जाता है, जैसाकि चित्र में दखाया गया है। यह x-सीधा में l दूरी चलकर प्लेट से टकराता है। चालकीय प्लेट का आवेश पृष्ठ घनत्व बराबर है
View Solutionएक बड़ा अचालक गोला जिसकी त्रिज्या r है, इस पर वैद्युत आवेश Q यूनिट (मात्रक) है, इसे एक छोटे अचालकीय अनावेशित r' त्रिज्या के गोले के पास रखा जाता है अब छोटे गोले पर आवेश होगा
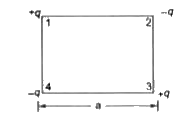
View Solutionएक a भुजा वाले वर्ग के चारो कोनो पर चित्रानुसार आवेश रखने में किया गया कार्य है
View Solutionयदि एक बिन्दु आवेश q को एक खोखले चालकीय गोले के अन्दर रखा जाता है, तब निम्नलिखित में से वैद्युत बल रेखाओं का कौन-सा निरूपण सही है?
View Solutionएक समान्तर प्लेट संधारित्र की प्लेटों के बीच `K_(1)` व `K_(2)` परावैद्युतांक की दो स्लैब रखी गई है जिसमे प्रत्येक की मोटाई `(d)/(2)` है। संधारित्र की प्लेटों के बीच की दूरी d है। संधारित्र की धारिता है
View Solutionदिय गए चित्र में x तथा y के बीच तुल्य धारिता है, `C_(2)=10muF` तथा अन्य संधारित्रों की धारिता `4muF` है
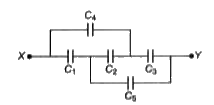
View Solutionचार संधारित्र, जिनमे प्रत्येक की धारिता `25muF` है, चित्रानुसार जोड़े गए है। DC वोल्टमीटर 200 वोल्ट मापता है, संधारित्र की प्रत्येक प्लेट का आवेश है
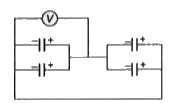
View Solutionदो संधारित्र एक `10muF` तथा दूसरा `20muF` का श्रेणी क्रम में 200 वोल्ट की सप्लाई लाइन से जुड़े हुए है। आवेशित संधारित्र इस लाइन से हटाए जाते है तथा इनकी धनात्मक प्लेटें तथा ऋणात्मक प्लेटें आपस में जोड़ी जाती है। यदि कोई बाह्य वोल्टेज नहीं लगाया जाता है। तो प्रत्येक संधारित्र का विभवांतर है
View Solutionएक समान्तर प्लेट संधारित्र जिसकी n बराबर दूरी पर रखी एकान्तर प्लेटों को बीच धारिता x है, तब कुल धारिता है
View Solutionछः एकसमान संधारित्र समान्तर क्रम में जुड़े है तथा अलग-अलग 10 वोल्ट विभवांतर से आवेशित किय जाते है। संधारित्र श्रेणी क्रम में इस प्रकार जोड़े जाते है कि एक की धनात्मक प्लेट दूसरे की ऋणात्मक प्लेट से सम्बन्धित है। तब मुक्त प्लेटों के बीच विभवांतर है
View Solutionयदि किसी पृष्ठ पर `underset(S)ointE.dS=0` है, तब
View Solutionएक धनावेश Q, एक पतली धात्विक गोलाकार वलय के केन्द्र पर रखा जाता है। सही कथन चुनो
View Solutionएक वृत्ताकार वलय जिसकी त्रिज्या R है, पर q आवेश समान रूप से वितरित है, यह yz-समतल में इस प्रकार रखी है, कि इसका केन्द्र मूल बिन्दु पर है। निम्नलिखित में से सही कथन ज्ञात करो
View Solutionकिसी बिन्दु पर वैद्युत क्षेत्र
View Solutionएक समान्तर प्लेट संधारित्र जिसका प्लेट क्षेत्रफल A तथा प्लेटों के बीच की दूरी d है, विभवांतर V तक आवेशित किया गया तथा फिर बैटरी को हटा दिया गया। इसके बाद संधारित्र की प्लेटों के बीच परावैद्युतांक K की पट्टी रखी गई जिसने प्लेटों के बीच का स्थान भर दिया। यदि प्रत्येक प्लेट पर आवेश का परिमाण q हो, प्लेटों के बीच वैद्युत क्षेत्र E हो (पट्टी रखने के बाद) तथा पट्टी रखने में किया गया कार्य W हो, तब
View Solutionयदि विश्व में केवल एक ही प्रकार का आवेश हो तो
View Solutionएक समान्तर प्लेट संधारित्र एक बैटरी से जुड़ा है। एक नगण्य मोटाई की धात्विक चादर प्लेटों के बीच इनके केन्द्र पर रखी जाती है। निम्नलिखित में से कौन-सा कथन सत्य है?
View Solutionएक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट पर q आवेश है। अब संधारित्र बैटरी से जुड़ा है। निम्नलिखित में से कौन-सा कथन सत्य है?
View Solutionकिसी ऐसे क्षेत्र पर विचार कीजिए जिसमे विभिन्न प्रकार के आवेश है। परन्तु कुल आवेश शून्य है। इस क्षेत्र से बाहर के बिन्दुओं पर
View Solutionएक समांतर प्लेट संधारित्र को आवेशित किया जाता है तथा तब बैटरी को हटा दिया जाता है। यदि संधारित्र की प्लेटों को आगे की ओर अलग-अलग अचालकीय हत्थे से घुमाया जाता है, तब निम्नलिखित में से कौन-सा सत्य है?
View Solutionचित्र में आवेशों की व्यवस्था तथा R त्रिज्या के गॉसीय पृष्ठ, जिसके केन्द्र पर कोई आवेश Q है, पर विचार कीजिए, तब
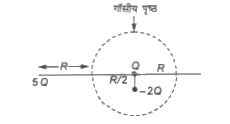
View Solutionएक अनन्त विस्तार की अचालकीय प्लेट S पर एकसमान आवेश घनत्व है। दो अनावेशित धात्विक छड़ A तथा B चित्रानुसार प्लेट के पास रखी है। निम्नलिखित में से कौन-सा कथन सत्य है?
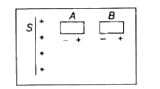
View Solutionएक बैटरी तथा कुंजी k से जुड़े एक धात्विक तार के चारो ओर एक बन्द पृष्ठ S खींचा गया है। कुँजी को दबाने पर, प्रवेश करने वाले प्रति सेकंड मुक्त इलेक्ट्रॉनों की संख्या बाहर निकलने वाले प्रति सेकंड मुक्त इलेक्ट्रॉनों की संख्या के बराबर है। बन्द पृष्ठ से बद्ध वैद्युत फ्लक्स
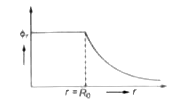
View Solutionसममित गोलीय आवेश वितरण के लिए वैद्युत विभव का केन्द्र से दूरी के साथ परिवर्तन चित्र में प्रदर्शित है। दिया है `phi_(r)=(q)/(4piepsilon_(0)r),(rgeR_(0))` के लिए `phi_(r)=(q)/(4piepsilon_(0)r),(rleR_(0))` के लिए कौन-से विकल्प सही है?
View Solutionकोई धनावेश Q किसी R त्रिज्या के वृत्ताकार लूप के अनुदिश एकसमान रूप से वितरित है। लूप के केन्द्र पर कोई छोटा परीक्षण आवेश q स्थित है, तब

View Solutionसमविभव पृष्ठ में एक आवेश को A से B तक ले जाने में किया गया कार्य है
View Solution
प्रश्नावली (स्तर 2 ) questions and complete solutions for chapter स्थिर वैद्युतिकी of ARIHANT PHYSICS (HINDI) of Class 12