Complete Solutions to EXERCISE -05 [B] (JEE ADVANCED : PREVIOUS YEAR QUESTIONS) of chapter 3D-COORDINATE GEOMETRY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | 3D-COORDINATE GEOMETRY |
| ALLEN HINDI | EXERCISE -05 [B] (JEE ADVANCED : PREVIOUS YEAR QUESTIONS) |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
(a) उस समतल का समीकरण ज्ञात कीजिए जो बिन्दुओं (2,1,0),(5,0,1) और (4,1,1) से गुजरता हो। (b) यदि बिन्दु P(2, 1, 6) है, तो बिन्दु Q ज्ञात कीजिए ताकि PQ, समतल (a) के लम्बवत् हो तथा PQ का मध्य बिन्दु उस पर स्थित हो।
View Solutionयदि रेखाएँ `(x-1)/2=(y+1)/3=(z-1)/4` तथा `(x-3)/1=(y-k)/2=z/1` परस्पर प्रतिछेद करती है, तो k का मान ज्ञात कीजिए।
View SolutionT एक समान्तर षटफलक है जिसमें एक फलक के शीर्ष A, B, C वD है। तथा इससे ठीक ऊपर के फलक के शीर्ष क्रमशः 'A', B, C, D' है। T को S तक इस प्रकार दबाया जाता है कि फलक ABCD समान रहे, तथा A', B, C, D', S क्रमशः A", B", C" व D" में स्थानान्तरित हो जाते है । का आयतन, T के आयतन का 90% कम हो जाता है। सिद्ध कीजिए कि "A" का बिन्दुपथ एक समतल होगा।
View Solutionएक समतल दो रेखाओं जिनके दिक् अनुपात (1, 0, -1) और (-1, 1, 0) है, के समान्तर है तथा यह (1,1, 1) से गुजरता है, यदि यह निर्देशी अक्षों को A, B, C पर काटता है, तो एक चतुष्फलक OABC का आयतन ज्ञात कीजिए, जहाँ O मूल बिन्दु है।
View Solutionएक चर समतल जो मूल बिन्दु से एक इकाई दूरी पर है तथा अक्षों को A, B, C पर काटता है। यदि त्रिभुज का केन्द्रक D(x, y, z) सम्बन्ध `1/x^(2) + 1/y^(2) + 1/z^(2) =k` को सन्तुष्ट करता है, तो k का मान होगा -
View Solutionरेखा `2x - y + z - 3 = 0, 3x + y + z = 5` को निहित करने वाले, बिन्दु (2, 1, -1) से 1/16 दूरी पर स्थित समतल का समीकरण ज्ञात कीजिए।
View Solutionएक समतल (1, -2, 1) से गुजरता है तथा समतल `2x -2y+ z= 0` तथा `x-y+2z = 4` के लम्बवत् है। इस समतल की बिन्दु (1, 2, 3) से लम्बवत् दूरी है|
View Solutionसुमेलित कीजिए :

View Solutionसुमेलित कीजिए :
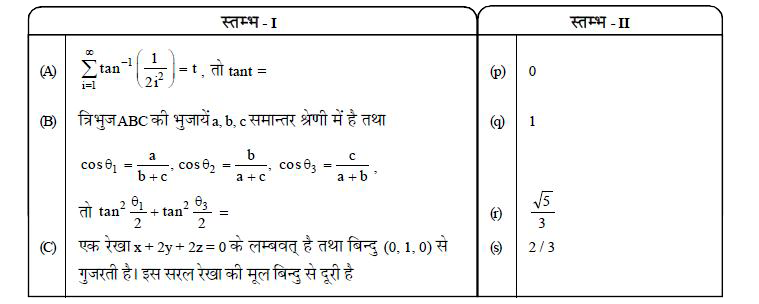
View Solutionमाना निम्न रेखीय समीकरण है:
`ax + by + cz =0, bx + cy + az=0, cx + ay + bz=0`

View Solutionमाना समतल `3x - 6y - 2z = 15` तथा `2x + y - 2z = 5` है।
कथन - 1 : दिये गए समतल की प्रतिच्छेद रेखा की प्राचल समीकरण `x=3 + 14t, y=1+ 2t, z=15 t` है। क्योंकि
कथन - 2 : सदिश `14hati + 2hatj + 15hatk` दिये गए समतल की प्रतिच्छेदी रेखा के समान्तर है।
View Solutionतीन समतल लीजिए
`P_(1) : x-y +z=1`
`P_(2): x+y -z=-1`
`P_(3): x-3y + 3z=2`
माना `L_(1), L_(2), L_(3)` क्रमशः समतल `P_(2)` व `P_3, P_3` व `P_(1)` तथा `P_(1)` व `P_(2)` की प्रतिच्छेदी रेखायें हैं।
कथन-1: `L_(1), L_(2)` और `L_(3)` में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।
View Solutionरेखाओं `L_(1):(x+1)/3=(y+2)/1=(z+1)/2, L_(2): (x-2)/1=(y+2)/2=(z-3)/3` पर विचार कीजिए।
दोनों रेखाओं `L_(1)` व `L_(2)` के लम्बवत इकाई सदिश है
View Solutionनिम्न रेखाएँ लीजिये ।
`L_(1): (x+1)/3 =(y+2)/1 = (z+1)/2, L_(2) , (x-2)/1 = (y+2)/2 = (z-3)/3`
रेखाओं `L_(1)` और `L_(2)` के बीच की न्यूनतम दूरी निम्न है:
View Solutionनिम्न रेखाएँ लीजिये ।
`L_(1): (x+1)/3 =(y+2)/1 = (z+1)/2, L_(2) , (x-2)/1 = (y+2)/2 = (z-3)/3`
बिन्दु (-1, -2, -1) से होकर जाने वाले तथा दोनों रेखाओं `L_(1)` व `L_(2)` के लम्बवत् अभिलम्ब वाले समतल की बिंदु (1, 1. 1) की दूरी निम्न है-
View Solutionधनात्मक दिक् कोज्याओं वाली एक रेखा बिन्दु P (2, -1, 2) से जाती है तथा निर्देशाक्षों से समान कोण बनाती है। यह रेखा समतल 2x+y+z = 9 से बिन्दु Q पर मिलती है। रेखा खण्ड PQ की लम्बाई निम्न है
View Solutionमाना P(3, 2. 6) आकाश में स्थित एक बिन्दु है तथा Q. रेखा `vecr =(hati - hatj + 2hatk) + mu(-3hati + hatj + 5hatk)` पर स्थित एक बिन्दु है। तब `mu` का मान जिसके लिए सदिश `bar(PQ)` समतल `x-4y+3z = 1` के समान्तर है, निम्न है:
View Solutionस्तम्भ I में दिए गए कथनों/व्यंजकों कोस्तम्भ II में दिए गए मानों के साथ सुमेलित कीजिए :

View Solutionसरल रेखा `x/2 = y/3 =z/4` को अतविष्ट करने वाले तथा, रेखाओं `x/3 = y/4 = z/2` तथा `x/4 =y/2 =z/3` को अत॑विष्ट करने वाले (containing) समतल के लम्बवत्, समतल का समीकरण निम्न है:
View Solutionयदि बिन्दु P(1,-2,1) से समतल `x + 2y - 2z =alpha` , जहाँ `a gt 0` की दूरी 5 है तो बिन्दु P से समतल पर डाले गए अभिलम्ब का पाद (foot) निम्न है:
View Solutionयदि समतल `Ax-2y+z=d` तथा रेखाओं `(x-1)/2=(y-2)/3=(z-3)/4` व `(x-2)/3=(y-3)/4=(z-4)/5` द्वारा बनाये गए तल के मध्य दूरी `sqrt(6)` है तो |d| का मान है
View Solutionकॉलम-1 में दिए वक्तव्यों का कॉलम-II में दिए गए संख्याओं से सुमेल करें।
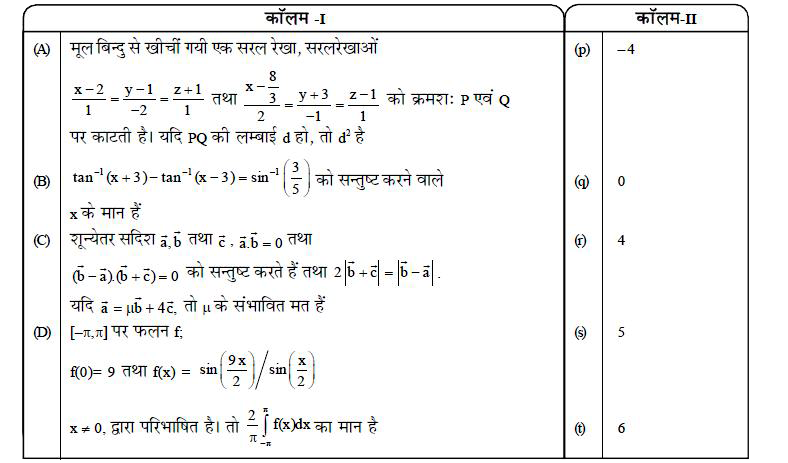
View Solutionबिन्दु P बिन्दुओं Q(2,3,5) और R(1,-1,4) से गुजरने वाली सरल रेखा एवं समतल `5x -4y- z = 1` का प्रतिच्छेदी बिंदु है। यदि बिंदु `T(2,1,4)` से QR पर डाले गये लम्ब का लम्ब-पाद S है तो रेखा-खण्ड PS की लम्बाई निम्न है .
View Solutionएक समतल, जो समतलों `x + 2y + 3z = 2` और `x - y + z = 3` की प्रतिच्छेदी-रेखा से गुजरता है और बिन्दु है (3, 1,-1) से `2/sqrt(3)` की दूरी पर है, का समीकरण निम्न है
View Solutionयदि सरल रेखाओं `(x-1)/2 = (y+1)/k = z/2` और `(x+1)/5 = (y+1)/2 = z/k` समतलीय (coplanar) है तो वह (वे) समतल जिसमे ये दोनों रेखाएं है, निम्न है (है)
View Solutionतल `x + y + z = 3` पर रेखा `(x+2)/2 = (y+1)/-1 = z/3` पर स्थित बिन्दुओं से लम्ब डाले जाते हैं। लम्ब-पाद निम्न रेखा पर स्थित हैं।
View Solutionएक रेखा l जो मूलबिन्दु से गुजरती है, रेखाओं
`l_(1) : (3+t)hati + (-1 + 2t)hatj + (4+2t)hatk, -infty lt t lt infty`
`l_(2) : (3+2s)hati + (3+2s)hatj + (2+s)hatk, -infty lt s lt infty`
पर लम्बवत है। तब l2, पर स्थित बिन्दु (बिन्दुओं) के निर्देशांक, जो रेखाओं l तथा `l_(1)` के प्रतिच्छेद बिन्दु से `sqrt(17)` की दूरी पर है (हैं), निम्न है (हैं) :
View Solutionदो रेखाएँ `L_(1): x =5, y/(3-alpha) =z/(-2)` तथा `L_(2): x= alpha, y/(-1) =z/(2-alpha)` समतलीय हैं। तब `alpha` का मान हो सकता है-
View Solutionरेखाएँ `L_(1) : (x-1)/2 =y/(-1) = (z+3)/1: L_(2) :(x-4)/1 = (y+3)/1 = (z+3)/2` तथा समतल `P_(1): 7x+y+2z=3, P_(2): 3x + 5y-6z=4` लीजिये। माना कि `ax + by + cz = d`, रेखाओं `L_(1)` व `L_(2)` के प्रतिच्छेद बिन्दु से गुजरने वाला तथा समतल `P_(1)` व `P_(2)` के लम्बवत् समतल का समीकरण है।
सूची-I को सूची-II से सुमेलित कीजिए तथा सूचियों के नीचे दिए नए कोड का प्रयोग करके सही उत्तर चुनिये:

View Solution
EXERCISE -05 [B] (JEE ADVANCED : PREVIOUS YEAR QUESTIONS) questions and complete solutions for chapter 3D-COORDINATE GEOMETRY of ALLEN HINDI of Class 12
All Exercises from ALLEN HINDI Class 12 MATHS 3D-COORDINATE GEOMETRY
- DO YOURSELF-1
- DO YOURSELF-10
- DO YOURSELF-2
- DO YOURSELF-3
- DO YOURSELF-4
- DO YOURSELF-5
- DO YOURSELF-6
- DO YOURSELF-7
- DO YOURSELF-8
- DO YOURSELF-9
- EXERCISE -01 (CHECK YOUR GRASP) (सही विकल्प चुनिए (केवल एक सही उत्तर है))
- EXERCISE -01 (CHECK YOUR GRASP) (सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं)
- EXERCISE -02 (BRAIN TEASERS) सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं)
- EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) कथन एवं कारण (Assertion & Reason)
- EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 1:
- EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 2:
- EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) गद्यांश आधारित प्रश्न (Comprehension Based Questions) गद्यांश # 3:
- EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) सत्य / असत्य (True False)
- EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) स्तम्भ सुमेलन (Match the column)
- EXERCISE -04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE)
- EXERCISE -04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)
- EXERCISE -05 [A] (JEE-[MAIN]: PREVIOUS YEAR QUESTIONS)
- EXERCISE -05 [B] (JEE ADVANCED : PREVIOUS YEAR QUESTIONS)
- उदाहरण