Complete Solutions to PROBLEM of chapter LAWS OF MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | LAWS OF MOTION |
| AAKASH SERIES | PROBLEM |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A body of mass 8kg is moved by a force F =3x N, where x is the distance covered . Initial position is x= 2m and final position is x = 10m . If initialy the body is at rest , find the final speed .
View SolutionIf a bullet of mass 5g moving withg a velocity of 100m/s penetrates a wooden block upto 6cm . Find the average force imposed .
View SolutionGive the magnitude and direction of the net force acting on
a drop of rain falling down with a constant speed
View SolutionGive the magnitude and direction of the net force acting on
a Cork of mass 10 g floating on water
View SolutionGive the magnitude and direction of the net force acting on
a kite skillfully held stationary in the sky
View SolutionGive the magnitude and direction of the net force acting on
a car moving with a constant velocity of 30km/h on a rough road
View SolutionGive the magnitude and direction of the net force acting on
a high - speed electron in space far from all material objects, and free of electric and magnetic field .
View SolutionA force of 100 dyne acts on a mass of 5 grams for 10 sec . Find the velocity produced ?
View SolutionGravel is dropped on a conveyer belt at the rate of 0.5 kg/ sec . Find the extra force required in Newton to keep the belt moving at 2m/sec.
View SolutionA body of mass 5kg starts from the origin with an initial velocity of `barU= (30i+40j)m//s`. A constant force of `F= (-hati - 5 hatj)N` acts on the body . Find the time in which they- component of the velocity becomes zero .
View SolutionA satellite in force free space sweeps stationary interplanetary dust at a rate `(dm)/(dt)= alphav` where m is mass , V is the velocity of the satellite and `alpha` is a constant . What is the decelration of the satellite .
View SolutionA solid sphere of mass 2 kg is resting inside a cube as shown in the figure . The cube is moving with a velocity v=5ti + 2tj . Here t is in second . All surface are smooth . The sphere is at rest with respect to the cube . What is the total force exerted by the sphere on the cube .
View SolutionTwo blocks of mass 4kg and 6kg are connected by a string as shown in the figure. They are initially at rest on the floor. Calculate their acceleration when a force of (a) 50N (b) 100N is applied on the pulley.
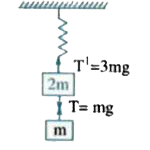
View SolutionThe system shown in the figure is in equilibrium at rest. The spring and string are massless Now the string is cut. Find the acceleration of the blocks just after the string is cut.
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
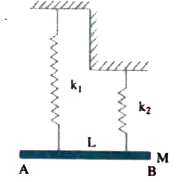
View SolutionFigure shows a block A on a smooth surface attached with a spring of force constant k to the ceiling. In this state spring is in its natural length l . The block A is connected with a massless and frictionless string to another identical mass B hanging over a light and smooth pulley. Find the distance moved by A before if leaves contact with the ground.

View SolutionFind the stretch in the springs shown in figure. The respective data are given in the figure. The friction and masses in pulleys are negligible. Find the extension in spring?

View SolutionFigure shows a box of mass m is placed on a wedge of mass 'M' on a smooth surface. How much force 'F' is required to be applied on 'M' so that during motion 'm' remains at rest on its surface.
View SolutionAn object of mass 3 kg is at rest . Now a force `F= 6t^(2) hati + 2thatj` is applied on the object . Find the velocity of the object at t =3 sec.
View SolutionIn the figure given below, the position - time graph of a particle of mass 0.1 kg is shown. Find impulse at t=2sec.
View SolutionA hunter has a machine gun that can fire 50g bullets with a velocity of `900 ms^(-1)`. A 40 kg tiger springs at him with a velocity of `10 ms^(-1)`. How many bullets must the hunter fire into the tiger in order to stop him in his track?
View SolutionA machine gun has a mass of 20kg. It fires 35 g bullets at the rate of 4 bullets per second, with a speed of `400 ms^(-1)`. What force must be applied to the gun to keep it in position?
View SolutionWith what acceleration 'a' should a box descend so that a block of mass M placed in it exerts force Mg/4 on the floor of the box?

View SolutionA 75kg man stands in a lift. What force does the floor exert on him when the elevator starts moving upward with an acceleration of `2 ms^(-2)` Given: g = `10 ms^(-2)`.
View SolutionFigure shows two blocks, each of mass 2kg, connected by a string passing over two pulleys. One block rests on a smooth horizontal surface and the other blockhangs vertically. Assume pullyes to be frictionless and massless. What is the tension in the string?

View SolutionThe pulley arrangements of figures (a) and (b) are identical. The mass of the rope is negligible. In figure (a), the mass m is lifted up by attaching a mass 2m to the other end of the rope. In figure(b), m is lifted up by pulling the other end of the rope with a constant downward force F = 2 mg. Calculate the accelerations in the two cases.
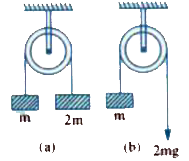
View SolutionFigure shows three blocks of mass m each hanging on a string passing over a pulley. Calculate the tension in the string connecting A to B and B toC?
View SolutionA rocket burns 50g of fuel per second ejecting it as a gas with a velocity of `5 xx 10 cm s^(-1)`. What force is exerted by the gas on the rocket?
View SolutionUsing constraint method find the relation between acceleration of 1 and 2.
View SolutionFind the constraint relation between `a_1, a_2 and a_3`.
View SolutionUsing constraint equations find the relation between `a_1 and a_2`

View SolutionA chain AB of length l is located on a smooth horizontal table so that its fraction of length h hange freely with end B on the table. At a certain moment, the end A of the chain is set free. With what velocity with this end of the chain slip off the table?

View SolutionA massless string passes over a frictionless pulley and carries mass `m_1` hanging at one end and mass `m_2` connected by another massless string to mass `m_3` at other end as shown in figure. Calculate the tension in string joining masses `m_2 and m_3`.
View SolutionA block A of mass 8 kg is placed on a frictionless horizontal table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 2 kg at the other end. Find the acceleration of the system. Also find the tension in the thread. If the thread is cut into two and tied to the ends of a spring of forceconstant 1600N/m, find the amount of stretching of the spring. Neglect the mass of thread and of spring `(g = 9.8 m//s^(2))`
View SolutionA monkey of mass m clings to a rope over a fixed pulley. The opposite ends of the rope is tide to a weight of mass M lying on a horizontal plate neglecting friction, find the acceleration of both bodies relative to the plate and tension of the rope in the following cases:
i) the monkey does not move with respect to rope.
ii) the monkey moves upwards with respect to rope with acceleration `beta` .
iii) the monkey moves downwards with respect to the rope with acceleration `beta`.
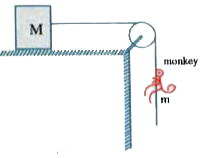
View SolutionReferring to figure calculate the downward acceleration of mass `m_1`. Assume the surfaces are frictionless and pullyes are massless.
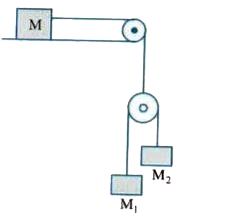
View SolutionThe pulley A and C are fixed while the pulley B is movable. A mass `M_2` is attached to pulley B , while the string has masses `M_1 and M_3` at the two ends. Find the acceleration of each mass .
View SolutionAt the moment t =0 , a force F = kt ( k is a constant) is applied to a small body of mass m resting on a smooth horizontal plane. The permanent direction of force F , makes an angle ` beta` with the horizontal . Calculate
i) The velocity of the body at the moment of its breaking off the plane .
ii) The distance traversed by the body upto this moment

View SolutionA smooth pulley A of mass `M_0` is lying on a smooth table. A light string passes round the pulley and has masses `M_1 and M_2 ` attached to its ends , the two portion of the string being perpendicular to the edge of the table so that the masses hang vertically . Calculate the acceleration of the pulley .
View SolutionA prism of mass M is placed on a horizontal surface. A block of mass m slides on the prism, which in tum slides on the horizontal surface. Assuming all surfaces to be frictionless, find the acceleration of block with respect to prism.

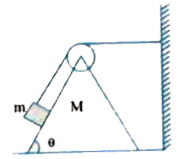
View SolutionA block of mass m is arranged on the wedge as shown in figure . The wedge angle is ` theta `. If the masses of pulley and thread and negligible and friction is absent , find the acceleration of the wedge
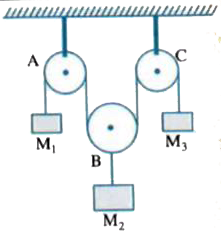
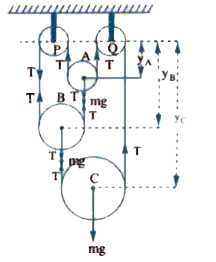
View SolutionIn the pulley system shown in figure. P and Q are fixed pulleys while A, B and C are movable pulleys each of mass 1kg. The strings are vertical and inextensible. Find the tension in the string and acceleration of frictionless pulleys A, B and C
View SolutionA system of four masses `m_1, m_2,m_3, m_4`, my two springs and a fixed pulley is shown in figure. The system is kept at rest by attaching the lower thread to a rigid peg. Determine the acceleration of all the masses after the lower thread has been cut. The springs are massless, pulley is frictionless and massless.
View SolutionA piece of uniform string hangs vertically so that its free end just touches horizontal surface of a table. The upper end of the string is now released. Show that at any instant during the falling of string, the total force on the surface is three times the weight of that part of string lying on the surface.
View SolutionA spherical rain drop, falling in a constant gravitational field, grows by absorption of moisture from the surroundings at a rate proportional to its surface area. If it starts with zero radius, find its acceleration.
View SolutionA flat car of mass m, starts moving to the right due to a constant horizontal force. Sand spills on the flat car from a stationary hopper. The velocity of loading is constant and equal to `mu` Kg/s. Find the time dependance of the velocity and the acceleration of the flat car in the process of loading. The friction is negligibly small.
View SolutionA rain drop of mass m, starts falling from rest and it collects water vapour and grows. If it gains `lambda` kg/s, find its velocity at any instant.
View SolutionA rocket is moving with constant acceleration 6. Assume external forces on it to be zero. Exhaust gases escape with velocity u relative to the rocket. Find how its mass changes with time if its initial mass is `m_0`.
View SolutionA body of mass 1 kg is moving with velocity `30 ms^(-1)` due north. It is acted on by a force of 10 N due east for 4 seconds. Find the velocity of the body after the force ceases to act.
View SolutionA very ftexible chain of length L and mass M is vertically suspended with its lower end just touching the table. If it is is released so that each link strikes the table and comes to rest, what force the chain will exert on table at the moment 'y' part of length falls on table ?
View SolutionMarbles each of mass 'm' are dropped from height 'h' on pan of a balance at the rate 'R' per sec. The balance calibrated in units of mass reads zero initially. If marbles are dropped continuously, what will the balance read after 't' sec ?
View SolutionThe variation of momentum with time of one of the body in a two body collision is shown. At what point the instantaneous force is maximum.
View SolutionA particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle at t = 1 s, 4 s and 7 s.
View SolutionGive the magnitude and direction of the net force acting on
(a) a drop of rain falling down with a constant speed
(b) a cork of mass 10 g floating on water
(c ) a kite skillfully held stationary in the sky
(d) a car moving with a constant velocity of 30 km/h on a rough road
(e ) a high - speed electron in space far from all material objects, and free of electric and magnetic fields.
View SolutionA pebble of mass 0.05 kg is thrown vertically upwards. Give the direction and magnitude of the net force on the pebble. [Ignore air resistance]
(a) during its upward motion
(b) during its downward motion
(c ) at the highest point where it is momentarily at rest.
Do your answer change if the pebble was thrown at an angle of `45^(@)` with the horizontal direction ?
View SolutionGive the magnitude and direction of the net force acting on a stone of mass 0.1 kg, [Neglect air resistance throughout].
(a) Just after it is dropped from the window of a stationary train
(b) just after it is dropped from the window of a train running at a constant velocity of 36 km/h.
(c ) just after it is dropped from the window of a train accelerating with 1 ms - 2
(d) lying on the floor of a train which is accelerating with 1 ms - 2, the stone being at rest relative to the train.
View SolutionA bob of mass 0.1 kg hung from the ceiling of a room by a string 2m long is set into oscillation. The speed of the trajectory of the bob if the string is cut when the bob is (a) at one of its extreme positions, (b) at its mean position.
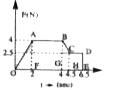
View SolutionA body of mass 2kg has an initial speed 5 m/s. A force acts as it for some time in the direction of motion. The force - time graph is shown in figure. Find the final speed of the body.
View SolutionA particle of mass 120 g moving at speed of 750 cm/s is acted upon by a variable force opposite to its direction of motion. If the velocity of the particle becomes 250 cm/s along the direction of force, find the value of time 't' for which acted.
View SolutionA bullet is fired from gun. The force on bullet is, `F = 600-2xx10^(5)t` newton. The force reduces to zero just when bullet leaves barrel. Find the impulse imparted to bullet.
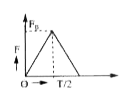
View SolutionA particle of mass m, moving with velocity 'u' makes head on collision with identical stationary particle, which is elastic. The force of interction increases to maximum and then becomes zero in time 'T' as shown in graph. What is the maximum value `F_(0)` of interaction force ?
View SolutionFigure shows the position - time graph of a particle of mass 4 kg, then
(a) force on the particle for `t lt 0, t gt 4s, 0 lt t lt 4 s` ?
(b) impulse at t = 0 and t = 4 s. (consider one - dimensional motion only)

View SolutionA ball of `sqrt(3)xx10^(-2)kg` hits a hard surface at `45^(@)` to normal with speed `4sqrt(2)m//s` and rebounds with `8//sqrt(3) m//s`, at `60^(@)` angle. If ball remains in contact for 0.1 sec, what force does it exert ?
View SolutionA gardener is watering plants at the rate 0.1 litre/sec using a pipe of cross - section `1 cm^(2)`. What additional force he has to exert if he desires to increase the rate of watering two times ?
View SolutionThe linear momentum of a particle varies with times as `p=a_(0)+at+bt^(2)`. Which of the following represents force and time relation ?
View SolutionA liquid of density `rho` flows along a horizontal pipe of uniform cross - section A with a velocity v through a right angled bend as shown in fig. What force has to be exerted at the bend to hold the pipe in equilibrium ?
View SolutionAssuming the gravity to be in negative z - direction, a force `vec(F)=vec(V)xx vec(A)` is exerted on a particle in addition to the force of gravity where `vec(V)` is the velocity of the particle and `vec(A)` is a constant vector in positive x - direction. What minimum speed a particle of mass m be projected so that it continues to move underflected with constant velocity ?
View SolutionExplain why a horse cannot pull a cart and run in empty space
View SolutionTwo ice skaters A and B approach each other at right angles. A has mass 30 kg and velocity 1 m/s and B has a mass of 20 kg and velocity 2 m//s. They meet and stick together. The final velocity of couple is :
View SolutionA man of mass m climbs a rope of length L suspended below a balloon of mass M. The balloon is stationary with respect to ground (a) if the man begins to climb up the rope at a speed `v_(rel)` (relative to rope) in what direction and with what speed (relative to ground) will the balloon move ? (b) How much has the balloon descended when the man reached the balloon by climbing the rope ?
View SolutionA dog weighing 5 kg is standing on a flat boat so that he is metre from the shore. He walks 4 metre on the boat toward shore and then halts. The boat weight 20 kg and one can assume that there is no friction between it and the water. How far is the dog from the shore at the end of this time ?
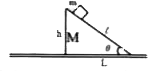
View SolutionAll surfaces are smooth. Find the horizontal displacements of the block and wedge when the block slides down from top to bottom.
View SolutionA man of mass M standing at a height h from the floor in a gravity free space throws a ball of mass m straight down with a speed u. When the ball reaches the floor, find the distance of the man above the floor.
View SolutionA bomb moving with velocity `40 hat(i)+50hat(j)+25hat(k)` m/s explodes into pieces of mass ratio 1 : 4. If the small piece goes out with velocity `200hat(i)+70 hat(j)-15hat(k)m//s`, find the velocity of larger piece after explosion.
View SolutionA body at rest explodes and breaks up into 3 pieces. Two pieces having equal mass, fly off perpendicular to each other with the same speed of 30 m/sec. The 3rd pieces has 3 times the mass of each of the other pieces. Find the magnitude and direction of its velocity immediately after the explosion.
View SolutionA shell fired a cannon with speed v m/s at angle `theta` with horizontal explodes into three pieces of equal masses at the highest point of trajectory. One piece falls down vertically while the other retraces its path. What is speed of the third piece ?
View SolutionA bomb of 1 kg is thrown vertically up with speed 100 m/s. After 5 seconds, it explodes into two parts. One of mass 400 gm goes down with speed 25 m/s. What will happen to the other part just after explosion
View SolutionA particle of 2m is projected at an angle of `45^(@)` with horizontal with a velocity of `20sqrt(2)m//s`. After 1 sec. explosion takes place and the particle is broken into two equal pieces. As a result of expansion one point comes to rests. The maximum height from the ground attained by the other part is `(g=10 m//s^(2))`
View SolutionA boy of mass 60 kg standing on a platform of mass 40 kg placed over a smooth horizontal surface. He throw, a stone of mass 1 kg with velocity u = 10 m/s at on angle of `45^(@)` w.r.t the ground. The displacement of platform (with boy) on the horizontal surface when the stone lands on the ground is `(g=10 m//s^(2))`
View SolutionAn isolated particle of mass m is moving in horizontal plane along the x - axis at a certain height above the ground. It suddenly explodes into two framents of masses `(m)/(4)` and `(3m)/(4)`. At an instant the smaller frament is at `y=+15 cm`. The larger fragment, at this instant is at
View SolutionA bomb initially at rest at a height of 40 m above the ground suddenly explodes into two identical fragments. One of them starts moving vertically downwards with an initial speed of 10 m/s. If acceleration due to gravity is `10 m//s^(2)`, the separation between the fragments, 2 seconds after the explosion is
View SolutionFuel is consumed at the rate of `50 kg s^(-1)` in a rocket. Find the thrust on the rocket if the velocity of the exhaust gases is `2 km s^(-1)`. Also calculate the velocity of the rocket at the instant, when its mass is reduced to 1/10th of its initial mass if its initial velocity is zero. (neglect gravity)
View SolutionThe first & second state of two stage rocket separately weight 100 kg and 10 kg and contain 800 kg and 90 kg fuel respectively. If the exhaust velocity of gases is 2 km/sec then find velocity of rocket (nearly `(log_(10)5=0.6990)` (neglet gravity).
View SolutionA mass of 3kg is suspended by a rope of length 2m from the ceiling. A force of 40N in the horizontal direction is applied at midpoint P of the rope as shown. What is the angle the rope makes with the vertical the equilibrium and the tension in part of string attached to the ceiling ? (Neglect the mass of the rope, `g=10m//s^(2)`)

View SolutionA mass of 1kg attached to one end of a string is first lifted up with acceleration `4.9 m//s^(2)` and then lowered with same acceleration. What is the ratio of tension in string in two cases
View SolutionA lift of mass 1000 kg moves up with an acceleration `1 ms^(-1)` in upward direction. Find the tension developed in supporting string.
View SolutionThe apparent weight of a man in a lift is `w_(1)` when lift moves upwards with some acceleration and is `w_(2)` when it is accelerating down with same acceleration. Find the true weight of the man and acceleration of lift.
View SolutionA lift is going up. The total mass of the lift and the passenger is 1500 kg. The variation in the speed of the lift is as shown in the figure. Find the tension in the rope pulling the lift at t = 11 th second.
View SolutionIn the above problem, find the height to which the lift takes the passenger.
View SolutionA 75 kg man stands in a lift. What force does the floor exert on him when the elevator starts moving upward with an acceleration of `2 ms^(-2)` Given : `g = 0 ms^(-2)`.
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration `a_(0)` with respect to the road. Find the angle made by the string with vertical at equilibrium. Also find the tension in the sting in this position.
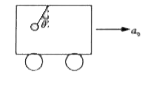
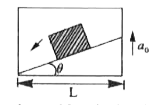
View SolutionA block slides down from top of a smooth inclined plane of elevation `theta` fixed in an elevator going up with an acceleration `a_(0)`. The base of incline has length L. Find the time taken by the block to reach the bottom.
View SolutionA block of mass m is pl aced on a smooth wedge of inclination `theta`. The whole system is accelerated horizontally so that the block does not slip on the wedge. Find the
(i) Acceleration of the wedge
(ii) Force to be applied on the wedge
(iii) Force exerted by the wedge on the block.
View SolutionAll surface are smooth. Find the acceleration of mass m relative to wedge when wedge is moving with acceleration 'a'

View SolutionFor what value of `'theta'` block slides up the plane with an acceleration 'g' relative to the inclined plane.
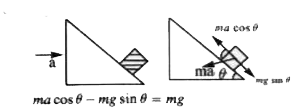
View SolutionFor what value of 'a' the block falls freely ?
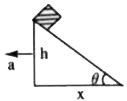
View SolutionInside a horizontally moving box, an experimenter finds that when an object is placed on a smooth horizontal plane and is released, it moves with an acceleration of `10 m//s^(2)`. In this box if 1 kg body is suspended with a light string, find the tenion in the string in equilibrium position (w.r.t experi-menter) `(g=10m//s^(2))`.
View SolutionA lorry carries a tank of water. If the lorry moves with a uniform acceleration 'a' in the horizontal direction, determine the angle made by the surface of water in the tank with the horizontal.
View SolutionA simple pendulum is suspended from the ceiling of trolley which is sliding down on a inclined plane of inclination `theta`. Find the angle made by the string with normal to the trolley (a) when trolley slides down with uniform velocity (b) when the plane is smooth.
View SolutionTwo blocks of masses 5 kg and 2 kg are kept in contact with each other on a frictionless horizontal surface. If a force of 14 N is applied on the larger block what is the acceleration of the system ? What is the contact force between the two blocks ?
View Solution
PROBLEM questions and complete solutions for chapter LAWS OF MOTION of JEE (MAIN AND ADVANCED) PHYSICS of Class 12