Complete Solutions to PROBLEMS (LEVEL - II) of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| AAKASH SERIES | PROBLEMS (LEVEL - II) |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
In Young's double slit experiment the y co-ordinates of central maxima and 10th maxima are 2 cm and 5 cm respectively. When the YDSE apparatus is immersed in a liquid of refractive index 1.5. Find the corresponding y co-ordinates.
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength `lamda` . Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionThe maximum intensity in Young's double slit experiment is `I_0` . Distance between the slits is d = `5lamda` , where `lamda` is the wavelength of monochromatic light used in the experiment. What will be the intensity of light in front of one of the slits on a screen at a distance D=10d ?
View SolutionIn a Young's double slit experiment the separation between slits is `2 xx 10^(-3)m` whereas the distance of screen from the plane of slits is 2.5m. Light of wavelengths in the range 2000-8000 Å is allowed to fall on the slits. Find the wavelengths in the visible region that will be present on the screen at `10^(-3)` m from the central maxima.
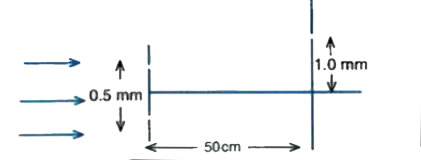
View SolutionWhite coherent light (400 nm-700nm) is sent through the slits of a Young's double slit experiment as shown in figure. The separation between the slits is 0.5mm and the screen is 50 cm away from the slits. There is a hole in the screen is 50 cm away from the slits. There is a hole in the screen at a point 1.0mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
View SolutionIn the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of onc of the interfering beams (wavelength `lamda` ), the intensity at the position where the central maximum occurred previously remains unchanged. Find the minimum thickness of the glass-plate.
View SolutionA two slit Young's interference experiment is done with monochromatic light of wavelength 6000 Å. The slits are 2 mm apart. The fringes are observed on a screen placed 10 cm away from the slits. Now a transparent plate of thickness 0.5 mm is placed in front of one of the slits and it is found that the interference pattern shifts by 5 mm. What is the refractive index of the transparent plate?
View SolutionThe Young's double slit experiment is done in a medium of refractive index 4/3. A light of 600 nm wavelength is falling on the slits having 0.45 mm separation. The lower slit S, is covered by a thin glass sheet of thickness `10.4mum` and refractive index 1.5. The interference pattern is observed on a screen placed 1.5m from the slits as shown. Find the location of central maximum (bright fringe with zero path difference) on the screen
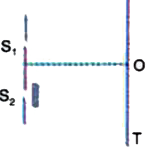
View SolutionTwo coherent point sources `S_1` and `S_2` vibrating in phase emit light of wavelength `lamda`. The separation between the sources is `2lamda` . Consider a line passing through `S_2` and perpendicular to the line `S_1 S_2`. What is the smallest distance from `S_2` where a minimum of intensity occurs?
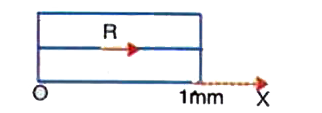
View SolutionThe figure shows a transparent slab of length 1mm placed in air whose refractive index in x direction varies as `mu = 1 +x^2 (0 lt= x lt =1)` (a) Find the optical path length of ray R. (b) If that slab is used in YDSE, it is placed infront of one of the slit. Find the shift in central maxima. (D=0.5 m, d = 2mm)
View SolutionIn figure S is a monochromatic point source emitting light of wave length `lamda` = 500nm. A thin convex lens of focal length 0.10m is cut into two identical halves `L_1` and `L_2` along the principal axis. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to `L_1` and `L_2` is 0.15m while that from `L_1` and` L_2` to O is 1.30 m. The screen at O is normal to SO.
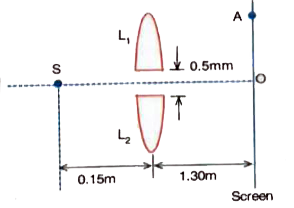
(a) If the third intensity maximum occurs at the point A on the screen, find the distance OA. (b) If the gap between `L_1` and `L_2` is reduced from its original value of 0.5 mm. Will the distance OA increase, decreases or remain the same?
View SolutionA source of light of wavelength 5000 A is placed in situation as shown in figure. Considering interference of direct and reflected rays, determine the position of the region where the fringes will be visible and calculate the number of fringes.

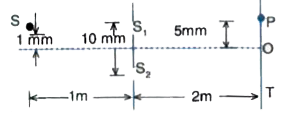
View SolutionIn the Young's double slit experiment a point source S of `lamda = 5000Å` is placed slightly off the central axis as shown in the figure. (a) Find the nature and order of the interference at the point P? (b) Find the nature and order of the interference at O. (c) Where should we place a film of refractive index `mu=1.5` and what should be its thickness so that maxima of zero order is placed at O.
View SolutionConsider the arrangement shown in figure. The distance D is large compared to the separation d between the slits.
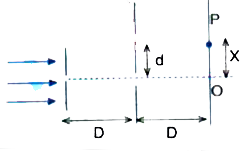
(a) Find the minimum value of d so that there is a dark fringe at 0. (b) Suppose d has this value. Find the distance x at which the next bright fringe is formed. (c) Find the fringe-width.
View SolutionLight of wavelength `lamda` = 500nm falls on two narrow slits placed a distance d = `50 xx 10^(-4)` cm apart, at an angle `phi = 30^@` relative to the slits shown in figure.
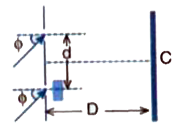
On the lower slit a transparent slab of thickness 0.1 mm and refractive index `3/2` placed. The interference pattern is observed on a distance D=2 m from the slits. Then calculate: (a) Position of the central maxima? (b) The order of minima closest to centre C of screen? (c) How many fringes will pass C, if we remove the transparent slab from the lower slit?
View SolutionEstimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
View SolutionThe aperture of a telescope is of 1m diameter and wavelength of light incident on the aperture is 5500Å. What is the angular limit of re solution of the telescope?
View SolutionCalculate the resolving power of a telescope whose objective lens has a diameter of 732 cm and `lamda = 6000Å`
View SolutionA horizontal beam of vertically polarized light o intensity `43 w//m^2` is sent through two polarizing sheets. The polarizing direction of the first is `60^@` to the vertical, and that of the second is horizontal. What is the intensity of the light transmitted by the pair of sheets?
View SolutionTwo polarizing sheets are placed together with their transmission axes crossed so that no light is transmitted. A third sheet is inserted between them with its transmission axis at an angle of` 45^@` with respect to each of the other axes. Find the fraction of incident unpolarized light intensity transmitted by the three sheet combination.
View Solution
PROBLEMS (LEVEL - II) questions and complete solutions for chapter WAVE OPTICS of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS WAVE OPTICS
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Integer Type Questions
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Linked Comprehension Type Questions)
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Matrix Matching Type Questions
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) More Than One Correct Answer Type Questions
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Straight objective Type Questions
- ADDITIONAL PRACTICE EXERCISE (LEVEL - I ) (MAIN) (Straight Objective Type Questions)
- Additional Practice Exercise (Level - I) (Main) Straight objective type questions
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Integer Type Quesiton)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Linked Comprehension Type Questions)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Matrix Matching Type Questions)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (More Than one correct Type Questions)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Straight Objective Type Questions)
- Additional Practice Exercise (Practice Sheet (Advanced))
- ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED ) Straight Objective Type Questions)
- EXAMPLE
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Linked Comprehension type questions
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Matrix Match Type Questions
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) More than one correct answer type questions
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) (straight objective Type Questions)
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Level - II (straight objective Type Questions) Integer Type Questions
- LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) (Straight objective Type questions)
- LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) Level - II (Straight objective type questions)
- LECTURE SHEET Exercise - III POLARLISATION (Level-II (Straight objective Type questions))
- LECTURE SHEET Exercise - III POLARLISATION(Level - I (Main) (Straight objective Type questions))
- LECTURE SHEET EXERCISE-I (LEVEL -I) (MAIN) straight objective Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Interger Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Linked Comprehension Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Matrix Matching Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) More than one correct answer Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED )staright Objective Type Questions
- LECTURE SHEET EXERCISE-II (LEVEL -I) (MAIN) (Straight Objective Type Questions)
- LECTURE SHEET EXERCISE-II (LEVEL -II) (MAIN) (Straight Objective Type Questions)
- LECTURE SHEET EXERCISE-III (LEVEL -I) (MAIN) (Straight Objective Type Questions)
- LECTURE SHEET EXERCISE-III (LEVEL -II) (MAIN) (Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL I - MAIN)(Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED) (Integer Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED) (Linked Comprehension Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED) (Matrix matching Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED)(More than one correct answer Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED)(Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -II(LEVEL I - MAIN) (Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -II(LEVEL II - MAIN) (Straight Objective Type Questions)
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - 1 (Main) Straight Objective Type questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Linked Comprehension Type Questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Matrix Matching Type Questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) More than one correct answer type questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Straight Objective Type questions
- Practice Sheet Exercise - II (DIFFRACTION) (Level - I (Main) (Straight objective Type questions)
- Practice Sheet Exercise - II (DIFFRACTION)(Level - II ) (Straight objective Type questions)
- Practice Sheet Exercise - III (POLARISATION) (Level - I (Main) (Straight objective Type questions)
- Practice Sheet Exercise - III (POLARISATION) (Level - II) (Straight objective Type questions)
- PRACTICE SHEET EXERCISE-III (LEVEL -I) (MAIN) (Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE-III (LEVEL -II) (MAIN) (Straight Objective Type Questions)
- PROBLEMS (LEVEL - I)
- PROBLEMS (LEVEL - II)