Complete Solutions to EXAMPLE of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| AAKASH SERIES | EXAMPLE |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
A plane wave that falls on a barrier containing small circular opening of dimension d. What can be said about the behaviour of the wave if `(i) lamda lt lt d, (ii) lamda = d ,(iii) lamda gt gt d `
View SolutionAn obstacle such as a telephone pole can cast a clear shadow in the light from a distant source. No such effect is noticed for the sound from a distant car horn. Why?
View SolutionTwo coherent sources emit light waves which superimpose at a point where these can be expressed as `E_1 = E_0 sin (omega t + pi//4), E_2 = 2E_0) sin (omega t - pi//4)` where `E_1` and` E_2` are the electric strengths of the two waves at the given point. If I is the intensity of wave expressed by field strength `E_1` , find the resultant intensity.
View SolutionA beam of light considering of two wavelengths 6500Å and 5200Å is used to obtain interference fringes in a Young's double slit experiment. :) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 6500Å (ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide ? Distance a between the slits is 2 mm, distance between the slits and the screen D= 120 cm.
View SolutionMaximum intensity in YDSE is `I_0` . Find the intensity at a point on the screen where (a) the phase difference between the two interfering beams is `pi//3` . (b) the path difference between them is `lamda//4`
View SolutionTwo coherent sources are 0.15 mm apart and fringes are observed at 1 m away with monochromatic light of wavelength 6000Å. Find (a) the fringe width in air, (b) the fringe width in a liquid of refractive index 5/2.
View SolutionTwo coherent sources are 0.18 mm apart and the fringes are observed on a screen 80cm away. It is found that with a certain monochromatic source of light, the fourth bright fringe is situated at a distance of 10.8 mm from the central fringe. Calculate the wavelength of light.
View SolutionBichromatic light is used in YDSE having wavelengths, `lamda_1` = 400nm and `lamda_2` = 700nm. Find minimum order of `lamda_1` which overlaps with `lamda_2`
View SolutionYoung's double slit experiment is carried out using microwaves of wavelength `lamda` = 3 cm. Distance between the slits is d = 5 cm and the distance between the plane of slits and the screen is D= 100cm. (a) Find the number of maximas and (b) Their positions on the screen.
View SolutionIn YDSE, the two slits are separated by 0.1 mm and they are 0.5m from the screen. The wavelength of light used is 5000 Å. Find the distance between 7th maxima and 11th minima on the screen.
View SolutionAn interference is observed due to two coherent sources `S_1` placed at origin and `S_2` placed at `(0,3lamda,0)` . Here `lamda` is the wavelength of the sources. A detector Dis moved along the positive X-axis. Find x-coordinates (excluding x = 0 and x = `oo` ) where maximum intensity is observed.
View SolutionTwo coherent light sources A and B with separation `2 lamda` are placed on the x-axis symmetrically about the origin. They emit light of wavelength `lamda` . Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and with centre at the origin.
View SolutionA thin sheet of a transparent material` (mu = 1.60)` is placed in the path of one of the interfering beams in a YDSE using sodium light, `lamda` = 5890 Å. The central fringe shifts to a position originally occupied by the 12th bright fringe. Calculate the thickness of the sheet.
View SolutionA double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of 1mm and distance between the plane of slit and screen 1.33m. The slits are illuminated by a parallel beam of light whose wavelength in air is 6300 Å.
(a) Calculate the fringe width (b) One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring the adjacent minima on the axis.
View SolutionLight of wavelength `lamda = 500nm` falls on two narrow slits placed a distance `d = 50 xx 10^(-4) cm ` apart, at an angle `phi =30^@` relative to the slits as shown in figure. On the lower slit, a transparent slab of thickness 0.1 mm and refractive index 3/2 is placed. The interference pattern is observed on a screen at a distance D = 2m from the slits. Then calculate
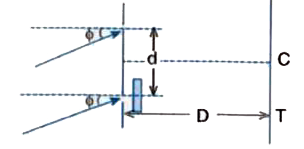
(a) position of the central maxima? (b) the order of minima closest to centre C of screen ? (c) How many fringes will pass over C, if we remove the transparent slab from the lower slit?
View SolutionA thin film is illuminated by wavelength 600 nm in free space at nearly normal incidence. Calculate the minimum thickness of a thin film (`mu` = 3/2 ) that results in constructive interference in the reflected light.
View SolutionA screen is placed 50 cm from a single slit, which is illuminated with 6000 Å light. If distance between the first and third minima in the diffraction pattern is 3.00 mm, what is the width of the slit ?
View SolutionIn a single slit diffraction experiment first minimum for, `lamda_1 = 660nm` coincides with first maxima for wavelength `lamda_2`. Calculate `lamda_2` .
View SolutionFor what distance is ray optics a good approximation when the aperture is 3 mm wide and the wavelength is 500 nm ?
View SolutionAssume that light of wavelength 6000Å is coming from a star. What is the limit of resolution of a telescope whose objective has a diameter of 100 inch?
View SolutionA microscope has objective of aperture 8 mm and focal length 2.5 cm. Estimate its resolving power. Given `lamda=5500Å `
View SolutionLight of wavelength 589 nm is used to view an object under a microscope. The aperature of the objective has a diameter of 0.900 cm. Find (a) The limiting angle of resolution. (b) What is the maximum limit of revolution for this microscope Using visible light of any wavelength you desire (c) What effect would this have on the resolving power. If water `(mu = 1.33)` fills the space between the object and objective.
View SolutionThe objective of a microscope has a focal length of 1 cm and diameter 0.5 cm. Using light of 6000 Å, is it possible to resolve the two point objects if they are separated by a distance of `10^(-6) m` ?
View SolutionWhen light of a certain wavelength is incident on a plane surface of a material at a glancing angle `30^@` , the reflected light is found to be completely plane polarized Determine a) refractive index of given material and b) angle of refraction.
View SolutionUnpolarized light falls on two polarizing sheets placed one on top of the other. What must be the angle between the characteristic directions of the sheets if the intensity of the transmitted light is one third intensity of the incident beam?
View SolutionA circular beam of light of diameter (width) falls on a plane surface of glass. The angle of incidence is 'i', angle of refraction is 'r' and refractive index of glass is `mu` . Then the diameter of the refracted beam d' is
View SolutionTwo polaroids are oriented with their planes perpendicular to incident light and transmission axis making an angle of `30^@` with each other. What fraction of incident unpolarized light is transmitted?
View Solution
EXAMPLE questions and complete solutions for chapter WAVE OPTICS of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS WAVE OPTICS
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Integer Type Questions
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Linked Comprehension Type Questions)
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Matrix Matching Type Questions
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) More Than One Correct Answer Type Questions
- Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Straight objective Type Questions
- ADDITIONAL PRACTICE EXERCISE (LEVEL - I ) (MAIN) (Straight Objective Type Questions)
- Additional Practice Exercise (Level - I) (Main) Straight objective type questions
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Integer Type Quesiton)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Linked Comprehension Type Questions)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Matrix Matching Type Questions)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (More Than one correct Type Questions)
- ADDITIONAL PRACTICE EXERCISE (LEVEL - II ) LECTURE SHEET (ADVANCED ) (Straight Objective Type Questions)
- Additional Practice Exercise (Practice Sheet (Advanced))
- ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED ) Straight Objective Type Questions)
- EXAMPLE
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Linked Comprehension type questions
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Matrix Match Type Questions
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) More than one correct answer type questions
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) (straight objective Type Questions)
- LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Level - II (straight objective Type Questions) Integer Type Questions
- LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) (Straight objective Type questions)
- LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) Level - II (Straight objective type questions)
- LECTURE SHEET Exercise - III POLARLISATION (Level-II (Straight objective Type questions))
- LECTURE SHEET Exercise - III POLARLISATION(Level - I (Main) (Straight objective Type questions))
- LECTURE SHEET EXERCISE-I (LEVEL -I) (MAIN) straight objective Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Interger Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Linked Comprehension Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Matrix Matching Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) More than one correct answer Type Questions
- LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED )staright Objective Type Questions
- LECTURE SHEET EXERCISE-II (LEVEL -I) (MAIN) (Straight Objective Type Questions)
- LECTURE SHEET EXERCISE-II (LEVEL -II) (MAIN) (Straight Objective Type Questions)
- LECTURE SHEET EXERCISE-III (LEVEL -I) (MAIN) (Straight Objective Type Questions)
- LECTURE SHEET EXERCISE-III (LEVEL -II) (MAIN) (Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL I - MAIN)(Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED) (Integer Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED) (Linked Comprehension Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED) (Matrix matching Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED)(More than one correct answer Type Questions)
- PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED)(Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -II(LEVEL I - MAIN) (Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE -II(LEVEL II - MAIN) (Straight Objective Type Questions)
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - 1 (Main) Straight Objective Type questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Linked Comprehension Type Questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Matrix Matching Type Questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) More than one correct answer type questions
- Practice Sheet (Exercise - I) (INTERFERENCE & YDSE) (Level - II (Advanced) Straight Objective Type questions
- Practice Sheet Exercise - II (DIFFRACTION) (Level - I (Main) (Straight objective Type questions)
- Practice Sheet Exercise - II (DIFFRACTION)(Level - II ) (Straight objective Type questions)
- Practice Sheet Exercise - III (POLARISATION) (Level - I (Main) (Straight objective Type questions)
- Practice Sheet Exercise - III (POLARISATION) (Level - II) (Straight objective Type questions)
- PRACTICE SHEET EXERCISE-III (LEVEL -I) (MAIN) (Straight Objective Type Questions)
- PRACTICE SHEET EXERCISE-III (LEVEL -II) (MAIN) (Straight Objective Type Questions)
- PROBLEMS (LEVEL - I)
- PROBLEMS (LEVEL - II)