Complete Solutions to PROBLEM of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| AAKASH SERIES | PROBLEM |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A magnetic field of `( 4.0 xx 10^(-3)hatk)` T exerts a force `( 4.0hati + 3.0hatj ) xx 10^(- 10)` N on a particle having a charge `10^(-9)` C and moving in the x-y plane. Find the velocity of the particle.
View SolutionA charged particle carrying charge `q = 1μC` moves in uniform magnetic field with velocity `v_(1) = 10^(6)`m/s at angle 45° with x-axis in x-y plane and experiences a force `F_(1)= 5sqrt2mN` along the negative z-axis. When the same particle moves with velocity, `v_(2) = 10^(6)` mis along the z-axis it experiences a force `F_(2)` in y-direction. Find
a) magnitude direction of the magnetic field
b) the magnitude of the force `F_(2)`.
View SolutionIf a particle of charge 1μC is projected into a magnetic field `vecB = (2hati + yhatj- zhatk)` T with a velocity `vecV = (4hati+2hatj - 6hatk)ms^(-1)`, then it passes undeviated. If it is now projected with a velocity `vecV = hati + hatj` , then find the force experienced by it?
View SolutionA particle of mass `m = 1.6 xx 10^(-27)` kg and charge `q = 1.6 xx 10^(-19)C` enters a region of magnetic field of strength 1 tesla along the, direction shown in figure. The speed of the particle is `10^(7)m//s`.
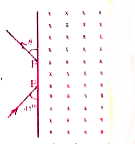
A) The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the field at the point F. Find the distance EF and the angle `theta`.
B) If the direction of the fie/ti is along the outward normal to the plane of the pape,, find the time spent by the particle in. the region of the magnetic field after entering it at E.
View SolutionAn ionized gas contains both +ve and -ve ions which are initially at rest. The gas is subjected to `vecE` toward positive x-axis, magnetic field along +ve z axis. Then.find the direction of deflection of
a) +ve charged ions b) -ve charged ions
View SolutionIn the figure, a charged sphere of mass m and charge q starts sliding from rest on a circular track of radius R from the position shown in the figure.
There exists a uniform and constant horizontal magnetic field of induction B. Find the maximum force exerted by the track on the sphere.

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is
`(mv)/(qB)`

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is
`(mv)/(2qB)`

View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is
`(2mv)/(qB)`

View SolutionA particle of charge q, mass m is moving in an electric field `vecE= EhatiNC^(-1)` and magnetic field `vecB =BhatkT` . It follows a trajectory from P to Q as shown Velocity at P is `Vhati` & that at Q is `- 2Vhatj`, find
a) electric field strength
b) power developed at P by electric field
c) rate of work done at by both fields at Q
View SolutionA particle of specific charge `alpha` starts moving from (0,0,0) under the action of electric field `E = chati` and magnetic field `vecB = B_(0)hatk`. Its velocity at (x, 0, 0) is `4hati + 3hatj`. Find the value of x
View SolutionTwo identical particles having the same mass m and charges +q and -q separated by a distance d entering a uniform magnetic field `vecB` as shown in the figure. For what value of d the particles will not collide.
View SolutionA cyclotron's oscillator frequency is 10 MHz. What should be the opertaing magnetic field for accelerating protons ? If the radius of its 'dees' is 60 cm, what is the kinetic energy (in MeV) of the proton beam produced by the accelerator.
`(e=1.60xx10^(-19)C, m_(p)=1.67xx10^(-27)kg, 1 MeV = 1.6xx10^(-13) J)`.
View SolutionA current carrying conductor of mass m, length I carrying a current i hangs by two identical springs each of stiffness k. For an outward magnetic field B find the deformation of the springs. Put m=50 gm,. `g=10m//s^(2),l=1/2m,i=1A` and B=1 T and k=50 N/m
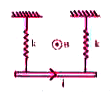
View SolutionFind the force experienced by the wire carrying a current 2A if the ends P and Q of the wire have coordinates (1,2,-3) m and (-2,-5,1)m respectively when it is placed in a magnetic field `B=(hati+hatj+hatk)T`
View SolutionA rod CD of length b carrying a current l, is placed in a magnetic field due to a thin log wire AB carrying currrent I as shown in fig. Then find the net force experienced by the wire
View SolutionA rough inclined plane inclined at angle `37°` with horizontal, has a metallic wire of length 20cm with its length `bot` to length, of inclined plane `( μ = 0.1)` When a current of i is passing through the wire and a magnetic field is applied normal to the plane upwards, the wire starts moving up with uniform velocity for B = 0.5T. Then find the magnitude of current i, (mass of the wire=50g)
View SolutionA wire PQ of mass 10g at rest on two parallel metal rails. The separation between the rails is 4.9cm. A magnetic field of 0.80 tesla is applied perpendicular to tlte plane of the rails, directed in wards. The resistance of the circuitis slowly decreased.
When the resistance decreases to below 20 ohm, the wire PQ begins to slide ou the rails. Calculate the coefficient of friction between the wire and the rails.
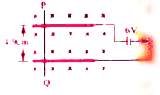
View SolutionTwo metal strips, each of length I, are clamped parallel to each other on a horizantal floor with a separation b between them. A wire of mass m lies on them perpendicular as shown in figure. A vertically upward magnetic field of strength B exists in the space. The metal strips are smooth but the coefficient of friction between wire and the floor is μ. A current i is established when the switch S is closed at the instant t = 0. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?
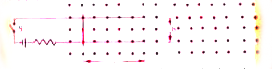
View SolutionAn element `Delta l = Delta x hati ` is placed at the origin and carries a large current I = 10 A . What is the magnetic field on the y-axis at a distance of 0.5 m. `Deltax = 1 cm. `
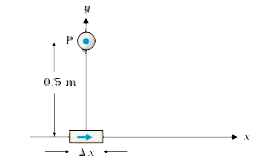
View SolutionThree rings, each having equal radius R, are placed mutually perpendicular to each other and each having its centre at the origin of coordinate system.
If current I is flowing through each ring then find the magnitude of the magnetic field at the common centre.

View SolutionTwo wires are wrapped over a wooden cylinder to form two coaxial loops carrying currents `i_(1)` and `i_(2)`. If `i_(2) = 8i_(1)` then find tlte value of x for B = 0 at the origin O
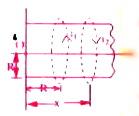
View SolutionA 2A current is flowing through a circular coil of radius 10 cm containing 100 turns. Find the magnetic flux density at the centre of the coil.
View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude and direction of magnetic field at O.
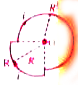
View SolutionTwo wires wrapped over a conical form the loops 1 and 2. If they produce no net magnetic field at the apex P, find the value of `(i_(1))/(i_(2))`

View SolutionA plastic disc of radius 'R' has a charge 'q ' uniformly distributed over its surface. If the disc is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA thin insulated wire form a spiral of N=100 turns carrying a current of i=8mA . The inner and outer radii are equal to a=5cm and b=10cm. Find the magnetic field at the centre of the coil.

View SolutionTwo circular coils made of same material having radii 20cm & 30cm have turns 1 00 & 50 respectively. If they are connected
a) in series b) in parallel
c) separately across a source of emf find the ratio of
magnetic inductions at the centres of circles in each case
View SolutionA charge of IC is placed at one end of a non conducting rod of length 0.6m . The rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency `10^(4)pi"rad"/s` . Find the magnetic field at a point on the axis of rotation at a distance of 0.8 m from the centre of the path
View SolutionTwo circular coils are made from a uniform wire the ratio of radii of circular coils are 2.3 & no. of turns is 3:4. If they are connected in parallel across a battery.
A.: Find ratio of magnetic induction at their centres.
B: Find the ratio magnetic moments of 2 coils
View SolutionThe magnetic induction due to the electron revolving in the first Bohr orbit of hydrogen atom at the centre of the orbit is B. If the electron is revolving in the second Bohr orbit the magnetic induction at the centre will be
View SolutionFigure shows a square current carrying loop ABCD of side 2cm and current `i=1/2A`. The magnetic moment M of the loop is

View SolutionFind the magnetic dipole moment of the spiral of total number of turns N, carrying current I having inner and outer radii v and b respectively

View SolutionIf two charged particles each of charge q mass m are connected to the ends of a rigid massless rod and is rotated about an axis passing through the centre and `bot` to length. Then find the ratio of magnetic moment to angular momentum
View SolutionA thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity `omega`. Find the ratio of its magnetic moment and angular momentum.
View SolutionConsider a non conducting plate of radius a and mass m which has a charge q distributed uniformly over it, The plate is rotated about its own axis with an angular speed `omega`. Show that the magnetic moment M and the angular momentum L of the plate are related as `M/L=q/(2m)`.
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionIf a straight conductor of length 40cm bent in the form of a square and the current 2A is allowed to pass through square, then find the magnetic induction at the centre of the square loop
View SolutionA large straight current carrying conductor is bent in the form of Lshape. Find B at P
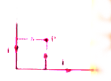
View SolutionIf a thin uniform wire of length 1m is bent into an equilateral triangle and carries a current of `sqrt3A` in anticlockwise direction, find the net magnetic induction at the centroid
View SolutionTwo thin long straight conductors have currents 4A and 1A carrying in the same direction which are arranged parallel with a separation of 2m. Then find a) position of neutral point
b) net magnetic induction at the midpoint between the 2 conductors
c) lf the direction of the current in one of the conductors is reversed then find the position of neutral point
View SolutionThree parallel long straight conductors are carrying equal currents i each as shown. Th e conductors are passing tlrrough the vertices of equilateral triangle of side 'a'.

Find the magnetic firld at C the centroid of triangle
View SolutionFind `vecB` at the origin due to the long wire carrying a current I

View SolutionA long straight current carrying conductor has a current from -z to +z, then find the magnetic induction at a point P(x, y, 0) in vectorial notation `(hati,hatj,hatk)` are unit vector along x,y, z axis)

View SolutionTwo wires AO and OC carry equal currents i as shown in the figure AOC = `theta`. Find the magnitude of the magnetic field at the point P on the bisector of an angle of `theta` at a distance 'r' from O. Assume that the other end of both wires extend to infinity

View SolutionSame current l is flowing through 3 infinite long thin wires along +ve x,y,z axes. Find the net magnetic induction at a point (0,0,-a) such that yz plane is in the plane of the paper (i,jk are the unit vectors along x,y and z axes respectively)
View SolutionInfinite number of straight wires each carrying current I are equally placed as sltown in the figure. Adjacent wires have current in opposite direction. Find net magnetic field at point P ?

View SolutionAn infinitely long wire carrying a current i is bent at its mid point O to form an angle 45°.l' is a point at a distance R from the point of bending . Find the magnetic field at P

View SolutionA pair of stationary and infinitely long bent wires are placed in the X·Y plane as shown in figure. The wires carry current of 10 ampere each as shown.
The segment L and M are along the X.axis. The segment P and Q are parallel to the Y-axis such that OS=OR=0.02m. Find the magnitude and direction of the magnetic induction at the origin O.

View SolutionFind the magnetic field at P due to the arrangement shown
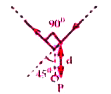
View SolutionAn equilateral triangle of side length l is formed from a piece of wire of uniform resistance. The current I as shown in figure. Find the magnitude of the magnetic field at its centre O.
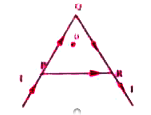
View SolutionA non planar loop of conducting wire carrying a current I is placed as shown in the figure each of the straight section of the loop is of length 2a. Find the direction of magnetic field due to this loop at the point P (a, 0, a)
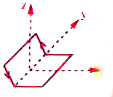
View SolutionA steady current is set up in a network composed of wires of equal resistance and length 'd' as shown in figure. What is the magnetic field at the centre P ?
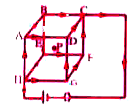
View SolutionA square metallic framee is made of 4 rods of same length 'a ' made of same material but rods, 1 and 2 are of thickness '2d ' & 3, 4 are of thickness d. If they are arranged as shown. Find the net magnetic induction at the point O .

View SolutionIf a very long thin wire is bent as shown carries a current i, then find `B_("net")` at the centre O of semicircular arc of radius r. which is in xy plane semi infinite wires connecting the arc in xz plane and also find the magnetic induction in vectorial from
View SolutionFind the magnetic field at centre P due to current i in the conductor as shown in fig.

View SolutionThe diagram shows three cases. In all the three cases the circular part has radius r and straight ones are infinitely long. For the same current, I find `bar(B)` at the centre P.

View SolutionFind magnetic field at O due to the current carrying conductor as shown in the figure.
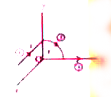
View SolutionA current I flows through an infinitly long wire having infinite brands as shown. The radius of the first curved section is a and the radii of the successive curved portions each increases by a factor `eta`. Find magnetic field at O.

View SolutionA wire carrying I has the confight-ration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, with all sections, both tangent to the same circle, with all sections lying in the same plane. What must `theta` be in order for B to be zero at the centre of the circle?

View SolutionA current I flows around a closed path in the horizontal plane of the circle as shown in the figure. The path consists of eight arcs witli alternating radii r and 2r.
Each segment of arc subtends equal angle at the common centre P. Find the magnetic field produced by current path at point P

View SolutionFind magnetic induction at C.

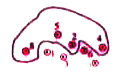
View SolutionEight wires cut the page perpendicular to the points shown. Each wire carries current irr Odd currents are out of the page and el'elt current into the page. Find the line integral `intovecB. Vecdl` along the loop.
View SolutionA solenoid 60 cm long and of radius 7.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis, both the wire and the ais of the solenoid are in the hoorizontal plane. The wire is connected through two lead parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire ? `g=9.8 m s^(-2)`.
View SolutionA solenoid of length 8cm has 500 turns /m in it. If radius of coil is 3cm and if it is carrying a current of 2A, find the magnetic induction at a point 4cm from the end on the axis of the solenoid
View SolutionA solenoid of 2m long & 3cm diameter has 5 layers of winding of 500 turns per metre length in each layer & carries a current of 5A. Find intensity of magnetic field at the centre of the solenoid.
View SolutionA toroid of non ferromagnetic has core of inner radius 25cm and outer radius 26cm. it has 3500 turns & carries a current of 1JA, then find the magnetic field at a point
i) In the internal cavity of toroid
ii) At the midpoint of the windings
iii) At a point which is at a distance of 30cm from the centre of toroid
View SolutionAn ideal solenoid having 40 turns/cm has an aluminium core and carries a current of 2.0 A. Calculate the magnetization l developed in the core and the magnetic field B at the centre. The susceptibility X of aluminimum `= 2.3 xx 10^(-5)`.
View SolutionA long, cylindrical iron core of crosssectional area 5.00 `cm^(2)` is inserted into a long solenoid having 2000 turns/m and carrying a current 2.00 A. The magnetic field inside the core is found to be 1.57 T. Neglecting the end effects, find the magnetization I of the core and the pole strength developed.
View SolutionA tightly-wound, long solenoid having 50 turns/cm, Carries a current of 4.00 A. Find the magnetic intensity Hand the magnetic field B at the centre of the solenoid. What will be the values of these quantities if an iron core is inserted in the solenoid and the magnetization l in the core is `4.00 xx 10^(6)` A/m?
View SolutionFind the percent increase in the magnetic field B when the space within a current-carrying toroid is filled with aluminium. The susceptibility of aluminium is `2.1 xx 10^(-5)`
View SolutionA toroid has a mean radius R equal to `20//pi` cm, and a total of 400 turns of wire carrying a current of 2.0A. An aluminium ring at temperature 280 K inside the toroid provides the cure. (a) If the magnetization I is `4.8 xx 10^(-2)` A/m, find the susceptibility of aluminium at 280 K. (b) If the temperature of the aluminium ring is raised to 320 K, what will be the magnetization ?
View SolutionA Long straight conductor carrying a current of 2 A is in parallel to another conductor of length 5 cm. and carrying a current 3A. They are separated by a distance of 10 cm. Calculate (a) B due to first conductor at second conductor (b) the force on the short conductor.
View SolutionTwo parallel horizontal conductors are suspended by light vertical threads 75.0 cm long. Each conductor has a mass of 40.0 gm per metre, and when there is 110 current they are 0.5cm apart. Equal magnitude current in the two wires result in a separatio11 of 1.5cm. Find the values and directions of currents.
View SolutionTwo conductors each of length 12 m lie parallel to each other in air. The centre to center distance between two conductors is `15 xx 10^(-2)` m and the current in each conductor is 300 amperes. Determine the force in newton tending to pull the conductors together.
View SolutionTwo parallel wires PQ, RS of resistance `10Omega` and `20Omega` are seperated by a distance of 10 cm and connected in parallel across a cell of emf200V and negligible intemal resistance. A wire AB of mass I g and length J cm is balanced exactly, between them. What must be the current in it.
View SolutionA conductor AB of length 10 cm at a distance of 10 cm from an infinitely long parallel conductor carrying a current 10A. What work must be done to move AB to a distance of 20cm if it carries 5A?
View SolutionA circular loop of area 1 `cm^(2)` carrying a current of 10A is placed in a magnetic field of 2 T i. The loop is in xy plane with current in clock wise direction. Find the torque on the loop
View SolutionGiven fig. shows a coil bent with all edges of length 1m and carrying a current of 1A. There exists in space a uniform magnetic field of 2T in the positive y-direction. Find the torque on the loop.
View SolutionA metallic wire is folded to form a square loop a side 'a'. It carries a current 'i' and is kept perpendicular to a uniform magnetic field. If the shape of the loop is changed from square to a circle withoul changing the length of the wire and current, the amount of work done in doing so is
View SolutionA loop carrying current 'i' is lying in the plane of the paper. It is in the field of a long straight wire with constant current `i_(0)` (inward) as shown in fig. Find the torque acting on the loop.

View SolutionA flat insulating disc of radius 'a' carries an excess charge on its surface is of surface charge density `sigma C//m^(2)`. Consider disc to rotate around the axis passing through its centre and perpendicular to its plane with angular speed `omega` rad/s. If magnetic field `vecB` is directed perpendicular to the rotation axis, then find the torque acting on the disc.
View SolutionThe area of the coil in a moving coil galvanometer is 16 `cm^(2)` and has 20 turns. The magnetic induction is 0.2T and the couple per unit twist of the suspended wire is `10^(-6)` Nm per degree. If the deflection is 45° calculate the current passing through it.
View SolutionA coil area 100 `cm^(2)` having 500 tums carries a current of 1 mA . It is suspended in a uniform magnetic field of induction `10^(-3) Wb//m^(2)`. Its plane makes an angle of 60° with the lines of induction. Find the torque acting on the coil.
View SolutionA galvanometer of resistance `20Omega` is shunted by a `2Omega` resistor. What part of the main current flows through the galvanometer ?
View SolutionA galvanometer has resistance 500 ohm. It is shunted so that its sensitivity decreases by 100 times. Find the shunt resistance.
View SolutionThe resistance of galvanometer is `999 Omega`. A shunt of `1Omega` is connected to it. If the main current is `10^(-2)A`, what is the current flowing through the galvanometer.
View SolutionA galvanometer has a resistance of `98Omega`. If 2% of the main current is to be passed through the meter what should be the value of the shunt?
View SolutionA maximum current of 0.5 mA can be passed through a galvanometer of resistance `20Omega`. Calculate the resistance to be connected in series to convert it into a voltmeter of range `(0- 5)V`.
View SolutionA galvanometer having 30 divisions has current sensitivity of 20 μA/ division. It has a resistance of 25 ohm. How will you convert it into an ammeter measuring upto 1 A? How will you now convert this ammeter into a voltmeter reading upto 1 V?
View SolutionA galvanometer has a resistance of `100Omega`. A current of `10^(-3)A` pass through the galvanometer. How can it be converted into (a) ammeter of range 10 A and (b) voltmeter of range 10v.
View SolutionWhat is the value of shunt which passes 10% of the main current through a galvanometer of 99 ohm?
View SolutionThe deflection in a moving coil galvanometer falls from 50 divisions to 10 divisions when a shunt of 12 ohm is applied. What is the resistance of the galvanometer?
View SolutionA galvanometer of resistance `95Omega` , shunted by a resistance of 5 ohm gives a deflection of 50 divisions when joined in series with a resistance of `20 kOmega` and a 2 volt accumulator. What is the current sensitivity of the galvanometer (in div / `muA` )?
View SolutionThe scale of a galvanometer is divided into 150 equal divisions. The galvanometer has the current sensitivity of 10 divisions per mA and the voltage sensitivity of 2 divisions per m V. How the galvanometer be designed to read (i) 6A, per division and (ii) 1 V, per division?
View SolutionA 100V voltmeter having an internal resistance of 20 `kOmega` is connected in series with a large resistance R across a 110 V line. What is the magnitude of resistance R if the voltmeter reads 5 V?
View SolutionA potential difference of 220 V is maintained across a 12000 ohm rheostat AB. The voltmeter V has a resistance of 6000 ohm and point C is at one fourth of the distance from A to B. What is the reading in the voltmeter?
View SolutionA galvanometer has an internal resistance of `50Omega` and current required for full scale deflection is 1 mA. Find the series resistances required [ as shown fig.]. to use it as a voltmeter with different ranges, as indicated in Fig.
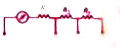
View SolutionTwo resistances of 100 ohm and 200 ohm are connected in series with a battery of emf 4 volt and negligible internal resistance. A voltmeter of resistance 200 ohm is used to measure voltage across the two resistances separately. Calculate the voltage indicated.
View SolutionA magnetic needle is arranged at the centre of a current carrying coil having 50 turns with radius of coil 20cm arranged along magnetic meridian. When a current of 0.5mA is allowed to pass through the coil the deflection is observed to be 30°. Find the horizontal component of earth's magnetic field
View Solution
PROBLEM questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of JEE (MAIN AND ADVANCED) PHYSICS of Class 12