Complete Solutions to PROBLEMS of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| AAKASH SERIES | PROBLEMS |
| Number Of Questions | 94 |
| Academic Year | 2023-24 |
A total of `6.0xx10^(16)` electrons pass through any cross - section of a conducting wire per second. Find the current.
View SolutionIn a hydrogen atom, electron moves in an orbit of radius `5 xx 10^(-11)` m with a speed of `2.2xx10^6` m/s . Calculate the equivalent current.
View SolutionThe current through a wire depends on time as `i=i_(0)+alphat`, where `i_(0)=10A` and `alpha=4A//s`. Find the charge crossed through a section of the wire in 10 seconds.
View SolutionA current is established in a discharge tube of cross section `8xx10^(-4)m^(2)` when a sufficiently high potential difference (say 32 kV) is applied across the two electrodes in the tube. The gas ionises, electrons move towards the positive terminal and positive ions towards the negative terminal. What are the magnitude and sense of the current in a hydrogen discharge tube in which `3xx10^(18)` electrons and `2xx10^(18)` protons move past the cross - sectional area of the tube in each second?
View SolutionConsider a wire of length 4m and cross - sectional area `1mm^(2)` carrying a current of 2A. If each cubic metre of the material contains `10^(29)` free electrons, find the average time taken by an electron to cross the length of the wire.
View SolutionPotential difference of 100 V is applied to the ends of a copper wire one metre long. Calculate the average drift velocity of the electrons ? Compare it with thermal velocity at `27^(@)C`. Consider there is one conduction electron per atom. The density of copper is `9.0xx10^(3)`, Atomic mass of copper is 63.5g. Avogadro's number `=6.0xx10^(23)` per gram - mole. Conductivity of copper is `5.81xx10^(7)Omega^(-1)`. Boltzmann constant `=1.38xx10^(-23)KJ^(-1)`.
View SolutionA wire has a resistance of `2.5Omega` at `100^(@)C`. Temperature coefficient of resistance of the material `alpha=3.6xx10^(-3)K^(-1)`. Find its resistance at `0^(@)C`.
View SolutionThe temperature coefficient of resistance of platinum is `alpha=3.92xx10^(-3)K^(-1)` at `0^(@)C`. Find the temperature at which the increase in the resistance of platinum wire is `10%` of its value of `0^(@)C`.
View SolutionResistance of a wire at temperature `t^(@)C` is `R=R_(0)(1+at+bt^(2))` Here, `R_(0)` is the temperature at `0^(@)C`. Find the temperature coefficient of resistance at temperature t is
View SolutionA silver wire has a resistance of `2.1 Omega` at `27.5^(@)C`, and a resistance of `2.7 Omega` at `100^(@)C`. Determine the temperature coefficient of resistivity of silver.
View SolutionA heating element using nichrome connected to a 230V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8A. What is the steady temperture of the heating element if the heating the room temperature is `27.0^(@)C`? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is `1.70 xx 10^(-4) .^(@)C^(-1)`.
View SolutionV - I graph of a conductor at temperature `T_(1) and T_(2)` are shown in the figure `(T_(2)-T_(1))` is proportional to
View SolutionA wire of silver has a resistance of 1 ohm. Specific resistance of constantan is 30 times the specific resistance of silver. Find the resistance of a constantan wire whose length is one third length of the silver wire and radius half the radius of the silver wire.
View SolutionA rectangular block has dimensions 5 cm `xx ` 5 cm `xx 10 cm ` . Calculate the resistance measured between (a) two square ends and (b) the opposite rectanglar ends specific resistance of the material is `3.5xx10^(-5)` `Omega` m
View SolutionTwo wires of same material have their lengths in the ratio 2:3 and radii 8:9 . Equal value of p.d is applied between their ends (separately). Calculate the ratio of current through those two
View SolutionFigure shows a conductor of length l having a circular cross - section. The radius of cross - section varies linearly from a to b. The resistivity of the materia is `rho`. Assuming that `b-a lt lt l`, find the resistance of the conductor.
View SolutionTwo wires A and B of same mass and material are taken. Diameter of wire A is half of wire B. If resistance of wire A is `24Omega` find the resistance of wire B.
View SolutionWhat will be the resistance of a semi circle shown in fig., between its two end faces. Given that radial thickness is 3cm, axial thickness is 4 cm, inner radius is 6 cm and specific resistance is `4xx10^(-6)" ohm "-cm`
View SolutionA hollow cylinder of specific resistance `rho`, inner radius R, outer radius 2R and length l is as shown in figure. What is the net resistance between the inner and outer surface?
View SolutionThere are two concentric spheres of radius (a) and (b) respectively. If the space between them is filled with medium of resistivity `rho`, then the resistance of the intergap between the two spheres will be
View SolutionA hollow copper cylinder is of inner radius 4cm and outer radius 5cm. Now hollow portion is completely filled with suitable copper wires. Find percentage change in its electric resistance.
View SolutionResistivity of the material of a conductor of uniform cross-section varies along its length as `rho=rho_(0)(1+alphax)`. Find the resistance of the conductor, if its length is l and area of corss-section A.
View SolutionHow many number of turns of nichrome wire of specific resistance `10^(-6)Omegam` and diameter 2mm that should be wound on a cylinder of diameter 5cm to obtain a resistance of ?
View SolutionSuppose the colours on the resistor as shown in Figure are brown, yellow, green and gold as read from left to right. Using the table, find the resistance of the resistor
View SolutionWhat is the color code for a resistor of resistance `350mOmega` with `5%` tolerance?
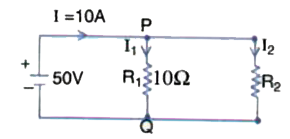
View SolutionFor a circuit shown in Fig. find the value of resistance `R_2` and current `I_2` flowing through `R_2`
View SolutionTwo wires of equal diameters of resistivities `p_1 and p_2` and length` x_1` and `x_2` respectively are joined in series. The equivalent resistivity of the combination is
View SolutionAn electric current is passed through a circuit containing two wires of the same material, connected in parallel. If lengths and radii of the wires are in the ratio of 4 : 3 and 2 : 3 , then ratio of the currents passing through the wires will be
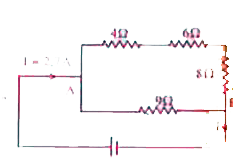
View SolutionFind equivalent resistance of the network in Fig. between points (i) A and B and (ii) and C.
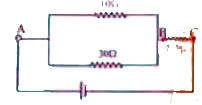
View SolutionFind potential difference between points A and B of the network shown in Fig. and distribution of given main current through different resistors.
View SolutionP and Q are two points on a uniform ring of resistance R. The equivalent resistance between P and Q is
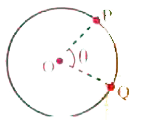
View SolutionDetermine the current drawn from a 12 V supply with internal resistance `0.5 Omega` by the infinite network shown in Fig. Each resistor has `1 Omega` resistance.

View SolutionIn the circuit shown in figure reading of voltmeter is `V_(1)` when only `S_(1)` is closed, reading of voltmeter is `V_(2)` when only `S_(2)` is closed and reading of voltmeter is `V_(3)` when both `S_(1) and S_(2)` are closed. Then
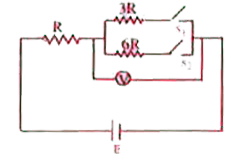
1) `V_(3) gt V_(2) gt V_(1)`
2) `V_(2) gt V_(1) gt V_(3)`
3) `V_(3) gt V_(1) gt V_(2)`
4) `V_(1) gt V_(2) gt V_(3)`
View SolutionIn the given network, calculate the potential difference between the points B and D
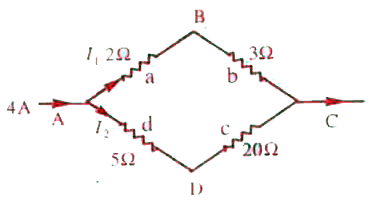
View SolutionFind out the value of current through `2Omega` resistance for the given circuit.
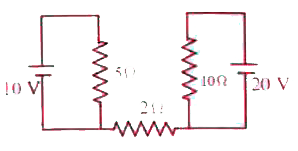
View SolutionA 1kW heater is meant to operate at 200 V. (a) What is its resistance ? (b) How much power will it consume if the line voltage drops to 100 V ? (c ) How many units of electrical energy will it consume in a month (of 30 days) if it operates 10 hr daily at the specified voltage?
View SolutionThree equal resistors connected in series across a source of emf together dissipate 10 watt of power. What would be the power dissipated if the same resistances are connected in parallel acrsoss the same source of emf?
View SolutionTo boil a certain mass of water, a coil will take a time of `t_(1)` and another coil will take a time of `t_(2)`. What will be the time taken when the coils are connected in (i) series (ii) in paralle?
View SolutionA lamp of 100 W works at 220 volts. What is its resistance and current capacity?
View SolutionA `100W-220V` bulb is connected to 110 V source. Calculate thepower consumed by the bulb.
View SolutionA 100 W and a 500 W bulbs are joined in series and connected to the mains. Which bulb will glow brigher ?
View SolutionA cell develops the same power across two resistance `R_(1) and R_(2)` separately. The internal resistance of the cell is
View SolutionA wire of length L and 3 identical cells of negligible internal resistances are connected in series. Due to the current, the temperature of the wire is raised by `DeltaT` in a time t. A number N of similar cells is now connected in series with a wire of the same material and cross - section but of length 2L. The temperature of the wire is raised by the same amount `DeltaT` in the same time. The volume of N is
View SolutionA heater is designed to operate with a power of 1000 watt in a 100 V line. It is connected in combination with a resistance of `10Omega` and a resistance R. to a 100 V mains as shown in the figure. What will be the value of R so that the heater operates with a power of 62.5 W?

View SolutionIn the circuit shown in figure the heat produced in the 5 ohm resistor due to the current flowing through it is 10 calorie per second. The heat generated in the 4 ohm resistor is
View SolutionA 100 W bulb `B_(1)` and two 60 W bulbs `B_(2)` and `B_(3)` are connected to a 250 V source, as shown in the figure. Now `W_(1), W_(2) and W_(3)` are the output powers of the bulbs `B_(1)B_(2) and B_(3)` respectively. Then
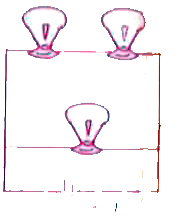
View SolutionAn electric bulb rated for 500 watt at 100 volt is used in a circuit having a 200 volt supply. The resistance R that must be put in series with the bulb, so that the bulb delivers 500 watt is ……….. Ohm.
View SolutionAn electric tea kettle has two heating coils. When one of the coils is switched on, boiling begins in 6 min. When the other coil is switched on, the boiling begins in 8 min. In what time, will the boiling begin if both coils are switched on simultaneously (i) in series and (ii) in parallel.
View SolutionIf two bulbs of 25 W and 100 W rated at 220 V are connected in series across 440 V supply. Will both the bulbs fuse? If not which one?
View SolutionA battery if internal resistance `4Omega` is connected to the network of ressitances as shown. What must be the value of R so that maximum power is delivered to the network? Find the maximum power?
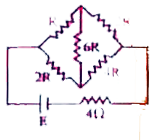
View SolutionA fuse wire with radius of 0.2mm blows off with a current of 5 Amp. The fuse wire of same material, but of radius 0.3 mm will blow off with a current of
1) `5xx(3)/(2)" Amp"`
2) `(5sqrt3)/(2)" Amp"`
3) `5sqrt((27)/(8))" Amp"`
4) 5 Amp
View SolutionA battery of emf 10 V internal resistance `3 Omega` is connected to a resistor R.
(i) If the current in the circuit is 0.5 A. calculate the value of R.
(ii) What is the terminal voltage of the battery when the cirucit is closed.
View SolutionWhen a current drawn from a battery is 0.5A, its terminal potential difference is 20V. And when current drawn from it is 2.0A, the terminal voltage reduces to 16V. Find out, e.m.f and internal resistance of the battery.
View SolutionAn ideal battery passes a current of 5A through a resistor. When it is connected to another resistance of `10Omega` in parallel, the current is 6A. Find the resistance of the first resistor.
View SolutionWhen a resistor of `11Omega` is conntected in series with an electric cell, the current flwoing in it is `0.5` A. Instead, when a resistor of `5Omega` is conntected to the same electric cell in series, the current increase by `0.4` A , The internal resistance of the cell is
View SolutionWhen a battery is connected to the resistance of `10Omega` the current in the circuit is 0.12 A. The same battery gives 0.07A current with `20Omega` Calculate e.m.f. and internal resistance of the battery.
View SolutionThe potential difference across the terminals of a battery is 10 V when there is a current of 3A in the battery from the negative to the positive terminal. When the current is 2A in the reverse direction, the potential difference becomes 15 V. The internal resistance of the battery is
View SolutionTwo cells A and B with same e.m.f of 2 V each and with internal resistances `r_(A)=3.5Omega` and `r_(B)=0.5Omega` are connected in series with an external resistance `R=3Omega`. Find the terminal voltage across the two cells.
View SolutionTwo cells A and B each of 2V are connected in series to an external resistance R = 1 ohm. The internal resistance of A is `r_(A)=1.9` ohm and B is `r_(B)=00.9` ohm. Find the potential difference between the terminals of A.
View SolutionIn the given circuit as shown below, calculate the magnitude and direction of the current
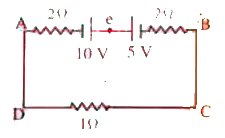
View SolutionTwo batteries each of emf E and internal resistance r are connected in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
View SolutionIn the steady state of the below given circuit, find the charge on the capacitor of capacity `0.2muF`.
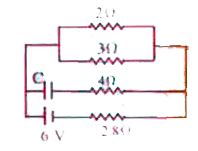
View SolutionTweleve celles each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. This battery is connected in series with an ammeter and two cells identical with each other. The current is 3A when the cells and battery aid each other and 2A when the cells and battery oppose each other. How many cells are wrongly connected?
View SolutionA voltmeter resistance `500Omega` is used to measure the emf of a cell of internal resistance `4Omega`. The percentage error in the reading of the voltmeter will be
View SolutionFind the emf (V) and internal resistance (r ) of a single battery which is equivalent to a parallel combination of two batteries of emfs `V_(1)` and `V_(2)` and internal resistances `r_(1)` and `r_(2)` respectively, with polarties as shown in figure
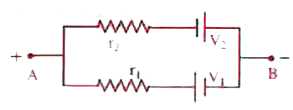
View SolutionConsider the network as shown in Fig. Current is supplied to the network by two batteries as shown. Find the values of currents `I_(1), I_(2), I_(3)`. The direction of the currents are as indicated by the arrows.
View SolutionFor the circuit shown in the figure, potential difference between points A and B is 16 V. Find the current passing through `2Omega`.
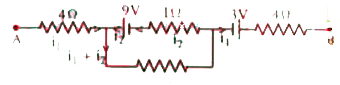
View Solution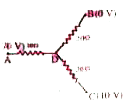
In the network shown A, B and C are at potentials of 70 V, zero V and 10 V respectively. The false one is
1) Point D is at a potential of 40 V
2) The currents in the sections AD, DB, DC are in the ratio `3:2:1`
3) The current in the section AD, DB, DC are in the ratio `1:2:3`
4) The network draws a total power of 200 W
View SolutionIn the given circuit values are as follows `epsilon_(1)=2V, epsilon_(2)=4V, R_(1)=1Omega` and `R_(2)=R_(3)=1Omega`. Calcualte the Currents through `R_(1), R_(2) and R_(3)`.
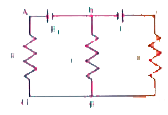
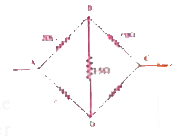
View SolutionThe given four terminal net work is a part of larger circuit. The points A, B, C are at the same potential. The P.E. between any one of A, B or C and D is 40 V. Find the P.D. between A & O.
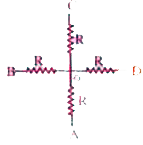
View SolutionSolve for current values in figure.
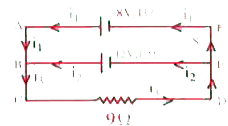
View SolutionFind the potential difference between and N in the given branch of a circuit figure.
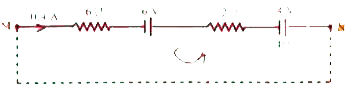
View SolutionTwo cells `E_(1)` (with emf 4V and internal resistance `2Omega`) and `E_(2)` (with emf 2V and intenral resistnace `2Omega`) are connected in parallel. The combination is connected in parallel with a `8Omega` resistance R as shown in figure. Calcualte the currents passing through 2V cell and through the resistance R.
View SolutionIn the given circuit, with steady current, the potential drop across the capacitor must be
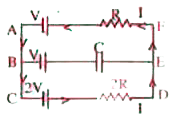
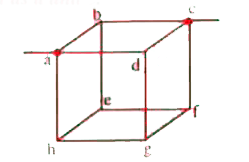
View SolutionFind the equivalent resistance of the circuit of the previous problem between the ends of an edge such as a and b in figure.
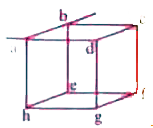
View SolutionTwelve equal wires, each of resistance r ohm are connected so as to form a skeleton cube. Find the equivalent resistance between the diagonally opposite points 1 and 7.
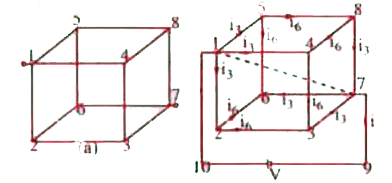
View SolutionTwelve wires, each having resistance r. are joined to form a cube as shown in figure. Find the equivalent resistance between the ends of a face diagonal such as a and c.
View SolutionDetermine the current in each branch of the network shown in fig.
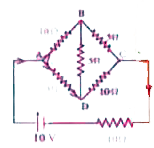
View SolutionFind the value of R in Fig. so that there is no current in the `15Omega` resistor.
View SolutionFind the Equivalent resistance across A and R in the given circuit if `r=10Omega, R=20Omega`.
View SolutionThe four arms of a Wheastone bridge (Figure) have the following resistance :
`AB=100Omega, BC=10Omega, CD=5Omega` and `DA=60Omega`
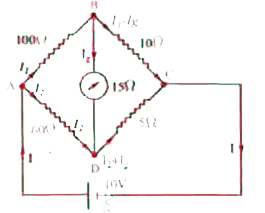
A galvanometer of `15Omega` resistance is connected across BD. Calculate the current through the galvano - meter when a potential difference of 10 V is maintained across AC,
View SolutionFind the effective resistance between P and Q points P and Q of the electrical circuit shown in the figure
View SolutionTwelve equal resistance are connected as shown in the diagram. Find the effective resistance between A and B
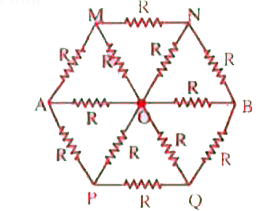
View SolutionIn the given circuit it is observed that the current I is independent of the value of theresistance `R_(5)`. Then what is the relation the resistance values must satisfy.
View SolutionA balance point in a meter bridge experiment is obtained at 30 cm from the left. If right gap contains `3.5Omega`, what is the resistance in the left gap?
View SolutionIn an metre bridge, the null point is found at a distance of 33.7 cm from A. If now a resistance of `2Omega` is connected in parallel with S, the null point occurs at 51.9 cm. Determine the value of R and S.
View SolutionIn the shown arrangement of the experiment of the meter bridge if AC corresponding to null defle-ction of galvanometer is x, what would be its value if the radius of the wire AB is doubled?
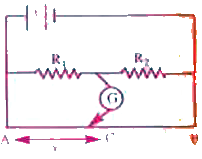
View SolutionA resistance of `2Omega` is connected across one gap of a metre-bridge (the length of the wire is 100 cm) and an unknown resistance, greater than `2Omega`, is connected across the other gap. When these resistances are interchanged, the balance point shifts by 20 cm. Neglecting any corrections, the unknown resistance is
View SolutionThe length of a potentiometer wire is 1m and its resistance is `4Omega`. A current of 5mA is flowing in it. An unknown source of e.m.f is the source.
View SolutionA resistance of `Romega` draws current from a potentiometer. The potentio - meter has a total resistance `R_(0)Omega` (Fig). A voltage V is supplied to the potentiometer.
Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
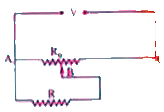
View SolutionIn a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of `10Omega` is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionA cell of e.m.f 2 volt and internal resistance `1.5Omega` is connected to the ends of 1m long wire. The resistance of wire is `0.5Omega//m`. Find the value of potential gradient on the wire.
View SolutionIn a potentiometer experiment when a battery of e.m.f. 2 V is included in the secondary circuit, the balance point is 500 cm. Find the balancing length of the same end when a cadimum cell of e.m.f. 1.018V is connected to the secondary circuit.
View SolutionFigure shows a 2.0 V potentiometer used for the determination of internal resistance of a 1.5 V cell. The balance point of the cell in open circuit is 76.8 cm. when a resistor of `9.5 Omega` is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell.
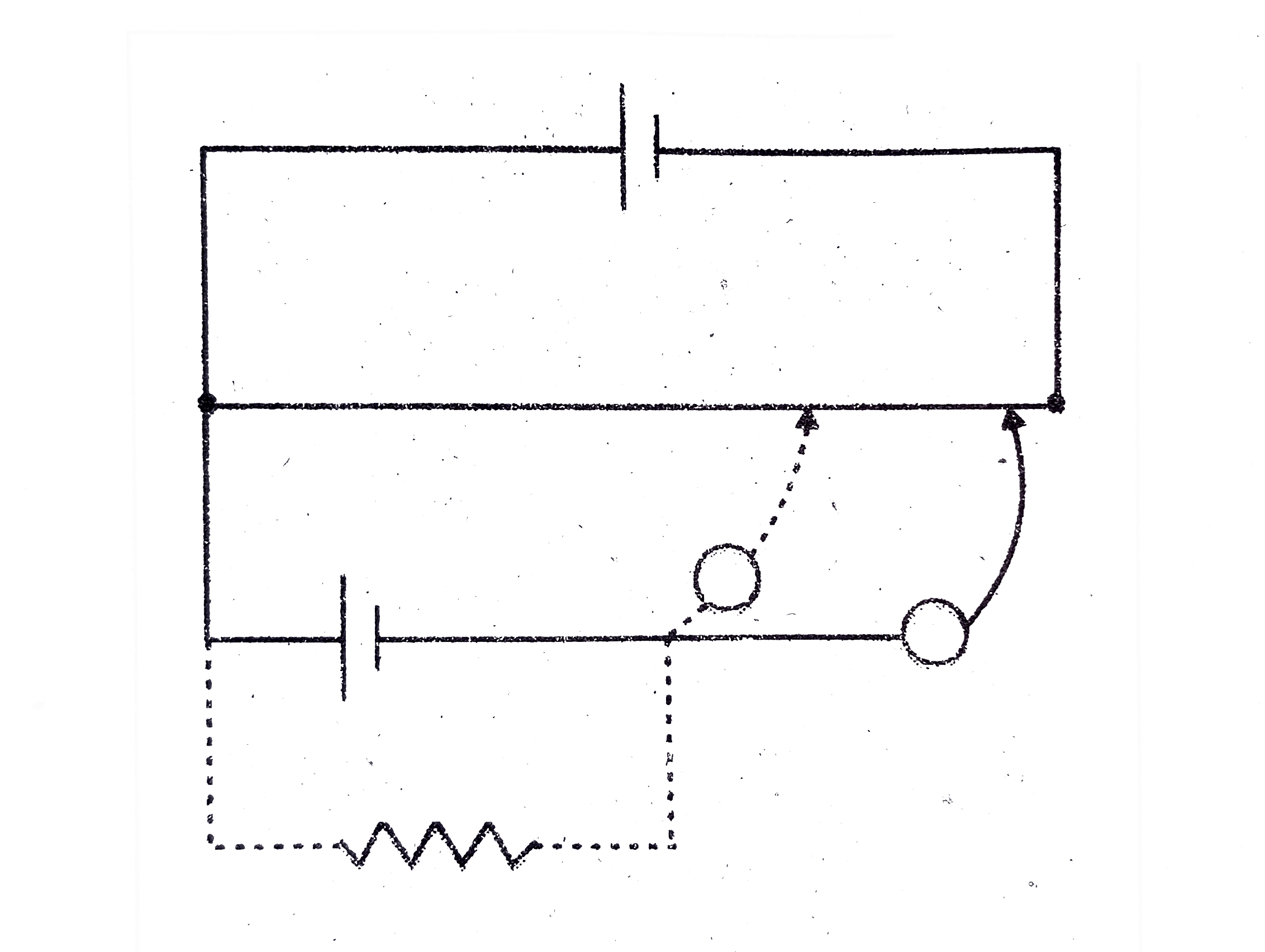
View Solution
PROBLEMS questions and complete solutions for chapter CURRENT ELECTRICITY of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS CURRENT ELECTRICITY
- ADDITIONAL PRACTICE EXERCISE (LEVEL -I(MAIN) (Straight Objective Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) (Integer Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) (Straight Objective Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (More than One correct answer Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions))
- EXERCISE - IA
- EXERCISE - IB
- EXERCISE - II
- EXERCISE - III
- LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
- LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Matrix Matching Type Questions))
- LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE- II LEVEL-I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (More than one correct answer type Questions))
- LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-I LEVEL-1(MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-III LEVEL- I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Linked Comprehension Type Questions)
- LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Matrix Matching Type Questions)
- LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Integer Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-V LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-V LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VI LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VI LEVEL- II (ADVANCED) (Matrix Matching Type Questions))
- LECTURE SHEET (EXERCISE-VI LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VII LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VII LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (Integer Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - II LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (Integer Type Questions))
- PRACTICE SHEET (EXERCISE - III LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
- PRACTICE SHEET (EXERCISE - IV LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (Integer Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VI LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VI LEVEL-II (ADVANCED) (More than One correct Type Questions))
- PRACTICE SHEET (EXERCISE - VI LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VII LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VII LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PROBLEMS