Complete Solutions to EXERCISE - III of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| AAKASH SERIES | EXERCISE - III |
| Number Of Questions | 73 |
| Academic Year | 2023-24 |
In a hydrogen tube it is observed that through a given cross-section `3.13xx10^(15)` electrons persec. moving from right to left and `3.12xx10^(15)` protons per sec are moving from left to right. The electric current in the discharge tube and its direction is
View SolutionAn electron of mass m, moves around the nucleus in a circular orbit of radius r under the action of centripetal force 'F'. The equivalent electric current is
View SolutionIn a straight conductor of uniform cross-section charge q is flowing for time t. Let s be the specific charge of an electron. The momentum of all the free electrons per unit length of the conductor, due to their drift velocity only is
View SolutionThe current density varies with radial distance r as `J=ar^(2)` in a cylindrical wire of radius R. The current passing through the wire between raidal distance `R//3` and `R//2` is
View SolutionA n-type silicon sample of width `4xx10^(-3)m`, thickness `25xx10^(-5)m` and length `6xx10^(-2)m` carries a current of 4.8 mA when the voltage is applied across the length of the sample. If the free electron density is `10^(22)m^(-3)`, then find how much time does it take for the electrons to travel the full length of the sample? Given that charge on an electron `e=1.6xx10^(-19)C`
View SolutionA hollow cylinder `(rho=2.2xx10^(-8)Omega-m)` of length 3 m has inner and outer diameters are 2 min and 4 mm respectively. The resistance of the cylinder is
View Solutionn conducting wires of same dimension but having resitives 1,2,3,…..n are connected In series . The equivalent resistivity of the combination is
View SolutionThe sides of rectangular block are `2cm, 3cm and 4 cm`. The ratio of the maximum to minimum resistance between its parallel faces is
View SolutionResistance of a wire is `8Omega`. It is drawn in such away that it experiences a longitudinal strain of `400 %`. The new resistance is
View SolutionA potential difference is applied between the ends of a conductor of uniform radius 1.5 mm. It results in an electric field of strength 250 V/m along the length of conductor. Find the resistivity of the material if current in the conductor is 2A.
View SolutionA potential difference of 30V is applied between the ends of a conductor of length 100 m and resistance `0.5Omega` . The conductor has a uniform cross-section. Find the total linear momentum of free electrons.
View SolutionAn electrical cable of copper has just one wire of radius 9 mm. Its resistance is 10 ohm. If this single copper wire of the cable is replaced by 6 identical well insulated copper wires each of radius 3 mm, what will be the new resistance of the cable?
View SolutionFind the value of colour coded resistance shown is fig

View SolutionThe colour coded carbon resistance has three bands. The bands from left are blue, yellow and red the resistance is
View SolutionA carbon resistor of `(47pm 4.7)kOmega` is to marked with rings of different colours for its identification. The colour code sequence will be
View SolutionTwo wires A and B of same material having their lengths in the ratio 6:1 are connected in series. The p.d. across the wires are 3V and 2V respectively. If `r_(B)//r_(A) and r_(B)` are radii of A and B respectively, `r_(B)//r_(A)` is
View SolutionThree resistance `2Omega, 3Omega and 5Omega` are connected in series and a p.d. of 20V is applied across the terminals of combination. The p.d. across `5Omega` resistance is
View SolutionTwo resistance of `400Omega` and `800Omega` are connected I series with 6 V battery of negligible internal resistance . A voltemeter of resistance `10000Omega` is used to measure the potential difference across `400Omega` The error in the measurement of potential difference in volt approximately is
View SolutionIn the steady state, the charge on the capacitor capacity `0.2muF` is
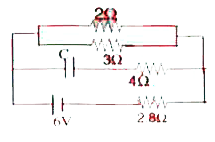
View SolutionIn the given circuit Ammeter reading is same when both switches `S_(1), S_(2)` are closed or opened . The value of resistance R is
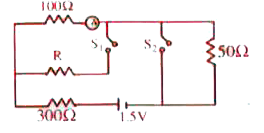
View SolutionThe resistance of the wire is 121 ohm. It is divided into .n. equal parts and they are connected in parallel, then effective resistance is 1 ohm. The value of .n. is
View SolutionThree unequal resistor in parallel are equivalent to a resistance `1Omega` If two of them are in the ratio 1:2 and if no resistance value is fractional the largest of the three resistance in ohm is
View SolutionTwo square metal plates A and B are of the same thickness and material. The side of B is twice that of A. These are connected as shown in series. If the resistances of A and B are denoted by `R_(A)` and `R_(B)` then `(R_(A)//R_(B))` is :
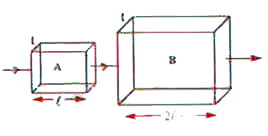
View SolutionA conductor of resistance `3Omega` is stretched uniformly till its length if doubled. The wire is now bent in the form of an equivalent triangle. The effective resistance between the ends of any side of the triangle in ohm is
View SolutionA,B and C are voltmeters of resistance R, 1.5 R and 3R respectively as shown in the fig. When some potential difference is applied between X and Y, the voltmeter reading are `V_(A), V_(B) and V_(C )` respectively.

View SolutionThe equivalent resistance between points A and B of an infinite network of resistance each of `1 Omega` connected as shown is
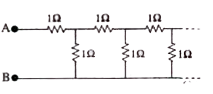
View SolutionEquivalent resistance across A and B in the given circuit is
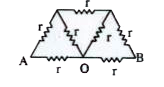
View SolutionEffective resistance between A and B in the given circuit it is
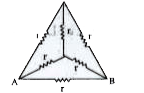
View SolutionA ring is made of a wire having a resistance `R_(0)=12Omega`. Find the points A and B, as shown in the figure, at which a current carrying conductor should be connected so that the resistance R of the subcircuit between these points is equal to `(8)/(3)Omega`
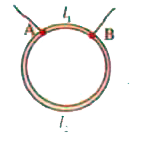
View SolutionAn aluminium `(alpha_(Al)=4xx10^(-3)//^(@)C)` wire resistance `'R_(1)'` and carbon wire `(alpha_(c)=0.5xx10^(-3)//^(@)C)` resistance `'R_(2)'` are connected in series to have a resultant resistance of 18 ohm at all temperatures The values of `R_(1) and R_(2)` in ohms
View SolutionA heating element using nichrome connected to a 230V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8A. What is the steady temperture of the heating element if the heating the room temperature is `27.0^(@)C`? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is `1.70 xx 10^(-4) .^(@)C^(-1)`.
View SolutionSame mass of copper is drawn into 2 wires of Imm thick and 3mm thick. Two wires are connected in series and current is passed. Heat produced in the wires is the ratio of
View SolutionMasses of three wires are in the ratio `1:3:5`. Their lengths are in the ratio `5:3:1`. When they are connected in series to an external source, the amounts of heats produced in them are in the ratio
View SolutionIn the following circuit, `5Omega` resistor develops 45 J/s due to current flowing through it. The power developed across `12Omega` resistor is
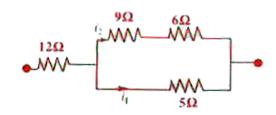
View SolutionTwo wires A and B of same material and mass have their lengths in the ratio `1:2`. On connecting them separately to the same source, the rate of heat dissipation in B is found to be 5W. The rate of heat dissipation in A is
View SolutionA cell of e.m.f E is connected to a resistance `R_(1)` for time t and the amount of heat generated in it is H. If the resistance `R_(1)` is replaced by another resistance `R_(2)` and is connected to the cell for the same time t, the amount of heat generated in `R_(2)` is 4H. Then the internal resistance of the cell is
View SolutionTwo cities are 150 km apart. Electric power is sent from one city to another city through copper wires. The fall of potential per km is 8 volt and the average resistance per km is `0.5Omega`. The power loss in the wire is
View SolutionIn a large building, there are 15 bulbs of 40W, 5 bulbs of 100W, 5 fans of 80W and 1 heater of 1kW. The voltage of the electric mains is 220 V. The minimum capacity of the main fuse of the building will be
View SolutionThe charge flowing through a resistance R varies with time t as `Q = at - bt^(2)`, where a and b are positive constants. The total heat produced in R is:
View SolutionWhen two identical cells are connected either in series or in parallel across a 4 ohm resistor, they send the same current through it. The internal resistance of the cell in ohm is
View SolutionTwo cells with same e.m.f. .E. and different internal resistances `r_(1)` and `r_(2)` are connected in series to an external resistance .R.. The value of R so that the p.d. across the first cell be zero is
View SolutionIf in the circuit shown below. The internal resistance of the battery is `1.5Omega` and `V_(P) and V_(Q)` are the potentials at P and Q respectively, the potential difference between the points P and Q is

View SolutionA 6 V cell with `0.5Omega` internal resistance , a 10 v cell with `1Omega` internal resistance and a `12Omega` external resistance are connected in parallel . The current (in amper) through the 10 V cell is
View SolutionFor a cell, the graph between the p.d.(V) across the terminals of the cell and the current I drawn from the cell is shown in the fig. the emf and the internal resistance of the cell is E and r respectively.
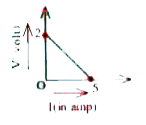
View SolutionHow many cells each marked `(6V-12A)` should be connected in mixed grouping so that it may be marked `(24V-24A)`
View SolutionThree equal resistance each of `3Omega` are in series and connected to cell of internal resistance one ohm. If three resistances are parallel and connected to the same cell. Then the ratio of the respective currents through the electric circuits in the two cases is
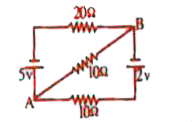
View SolutionThe P.d between the terminals A&B is
View SolutionEels are able to generate current with biological cells called electro plaques. The electroplaques in an eel are arranged in 100 rows, each row stretching horizontally along the body of the fish containing 5000 electroplaques. The arrangement is suggestively shown here. Each electroplaques has an emf of 0.15V and internal resistance of The water surrounding the eel completes a circuit between the head and its tail. If the water surrounding it has a resistance of the current an eеl can produce in water is about

View SolutionIn the circuit shown, current flowing through 25V cell is
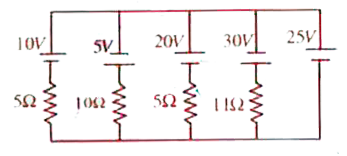
View SolutionA cell of emf `epsilon` and internal resistance r is connected across a variable load resistance R. The graph drawn between its terminal voltage and resistance R is
View SolutionThe current through `10Omega` resister in the figure is approximately
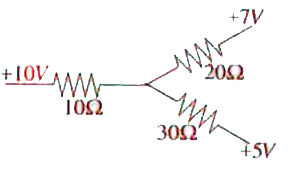
View SolutionA current of 3A flows in a circuit the potential difference between the junctions of `6Omega & 4Omega and 4Omega & 2Omega`.
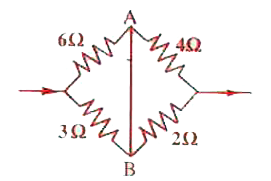
View SolutionA bettery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance `1Omega` Determine the equivalent resistance of the network and the current along each edge of the cube.
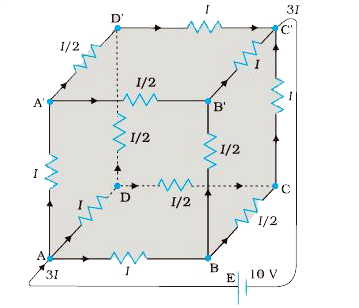
View SolutionIn the circuit shown in the figure, if potential at point A is taken to be zero, the potential at point B is
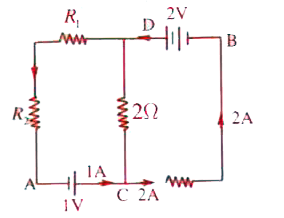
View SolutionThe current I drawn from the 5 volt source will be
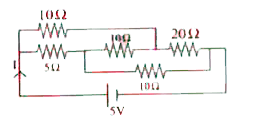
View SolutionA metallic conductor at `10^(@)C` connected in the left gap of meter bridge gives balancing length 40 cm. When the conductor is at `60^(@)C`, the balancing point shifts by ---cm, (temperature coefficient of resistance of the material of the wire is `(1//220)//""^(@)C)`
View SolutionWhen a conducting wire is connected in the right gap and known resistance in the left gap, the balancing length is 60cm. The balancing length becomes 42.4 cm when the wire is stretched so that its length increases by
View SolutionIn a metere bridge. The balance length from left end (standard resistance of `1Omega` is in the right gap) is found to be 20cm the length of resistance in left gap is 1/2 m and radius is 2mm its specific resistance is
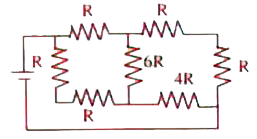
View SolutionA battery of internal resistance `4Omega` is connected to the network of resistances as shown in the fig. In order that the maximum power can be delivered to the network, the value of R in `Omega` should be
View SolutionIn a metre bridge , the gaps are enclosed by resistances of `2omega` and `3Omega` . The value of shunt to be added to `3Omega` resister to shift the balancing point by 22.5cm is
View SolutionThe resistances in the two arms of the mater bridge are `5Omega` and `ROmega`, respectively. When the resistance R is shunted with an equal resistance, the new balance point is at `1.6l_(1)` . The resistance 'R' is
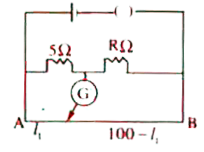
View SolutionA student finds the balancing length to be .l. with a cell of constant emf in the secondary circuit. Another student connects the same cell in the secondary circuit of potentio meterof double the length but with a cell of half the emf in the primary circuit. The balancing length will be [cell in primary is ideal and no series resistance is present in primary circuit]
View SolutionIn an experiment with potentiometer to measure the internal resistance of a cell, when the cell is shunted by `5Omega`, the null point is obtained at 2m. when cell is shunted by `20Omega` the null point is obtained at 3m. The internal resistance of cell is
View Solution1 ohm resistance is in series with an Ammeter which is balanced by 75cm of potentiometer wire. A standard cell of 1.02V is balanced by 50cm. The Ammeter shows a reading of 1.5A. The error in the Ammeter reading is
View SolutionA battery of negligible internal resistance is connected with 10m long wire. A standard cell gets balanced on 6m length of this wire. On increasing the length of potentiometer wire by 2m, the null point with the same standard cell in the secondary will be (no series resistance in primary)
View SolutionA potentiometer wire 10m long and having `20Omega` resistance is connected in series with a battery and a resistance `R = 2160Omega`. A daniel cell of emf 1.08 v is balanced across the P.D. of the resistance R. The emf of thermo couple is balanced across 300 cm of the wire. The emf of thermo couple is
View SolutionA potentiometer wire has resistance of 10 ohms. A resistance box with a resistance 19990 ohm is connected in series with the wire. The emf of the battery in the primary circuit is 2V. A thermo couple produces 2m V for a temperature difference `1^(@)C` between its jucntion. When the hot junction is at `200^(@)C` and cold junction at `0^(@)C`, can the thermo emf be balanced on the potentiometer wire?
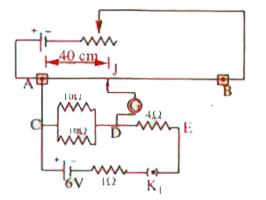
View SolutionIn the circuit shown in fig., the potential difference between the points C and D is balanced against 40cm length of potentiometer wire of total length 100cm. In order to balance the potential difference between the points D and E. The jockey be pressed on poten-tiometer wire at a distance of
View SolutionA thermocouple has its junctions at `0^(@)C` and `100^(@)C`. It produces 0.022mV/K. Find the balancing length on a potentiometer wire of 10m length and resistance `10Omega` connected in series with a resistance box consisting of a resistance of `1990Omega`. Given emf of cell in the primary circuit as 2 volt
View SolutionA potentiometer wire has length 4 m and resistance `8Omega`. The resistance that must be connected in series with the wire and an accumulator of e.m.f. 2V, so as to get a potential gradient 1 mV per cm on the wire is:
View SolutionA potentiometer wire is 100 cm long and a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obtained at 50 cm and 10 cm from the positive end of the wire in the two cases. The ratio of emf's is :
View SolutionA potentiometer is an accurate and versatile device to make electrical measurements of E.M.F. because the methods involves:
View SolutionA battery consists of a variable number n of identical cells having internal resistance connected in series. The terminals of the battery are short circuited and the current I measured.
Which one of the graph below shows the relationship between I and n?
View Solution
EXERCISE - III questions and complete solutions for chapter CURRENT ELECTRICITY of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS CURRENT ELECTRICITY
- ADDITIONAL PRACTICE EXERCISE (LEVEL -I(MAIN) (Straight Objective Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) (Integer Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) (Straight Objective Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (More than One correct answer Type Questions))
- ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions))
- EXERCISE - IA
- EXERCISE - IB
- EXERCISE - II
- EXERCISE - III
- LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
- LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Matrix Matching Type Questions))
- LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE- II LEVEL-I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (More than one correct answer type Questions))
- LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-I LEVEL-1(MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-III LEVEL- I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Linked Comprehension Type Questions)
- LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Matrix Matching Type Questions)
- LECTURE SHEET (EXERCISE-III LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Integer Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
- LECTURE SHEET (EXERCISE-IV LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-V LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-V LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VI LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VI LEVEL- II (ADVANCED) (Matrix Matching Type Questions))
- LECTURE SHEET (EXERCISE-VI LEVEL- II (ADVANCED) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VII LEVEL - I (MAIN) (Straight Objective Type Questions))
- LECTURE SHEET (EXERCISE-VII LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (Integer Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
- PRACTICE SHEET (EXERCISE - I LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - II LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (Integer Type Questions))
- PRACTICE SHEET (EXERCISE - III LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
- PRACTICE SHEET (EXERCISE - IV LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (Integer Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (More than One correct answer Type Questions))
- PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VI LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VI LEVEL-II (ADVANCED) (More than One correct Type Questions))
- PRACTICE SHEET (EXERCISE - VI LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VII LEVEL-I (MAIN) (Straight Objective Type Questions))
- PRACTICE SHEET (EXERCISE - VII LEVEL-II (ADVANCED) (Straight Objective Type Questions))
- PROBLEMS