Complete Solutions to PROBLEM of chapter WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVES |
| AAKASH SERIES | PROBLEM |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
Given below are some examples of wave motion. Statein each case if the wave motion is transverse, longitudinal or a combinatin of both.
(a) Motion of kink in a longitudinal spring produced by displacing one end of the spring sideways.
(b) Waves produced in a cylinder containing a liquid by moving its piston back and forth.
(c ) Waves produced by a motorboat sailing in water.
(d) Ultrasonic waves in air produced by a vibrating quartz crystal.
View SolutionA progressive wave of frequency 500 HZ is travelling with a velocity of 360`ms^(-1)`. The distance between the two points, having a phase difference of `60^(@)` is ………
View SolutionA longitudinal progressive wave is given by the equation `y = 5 xx 10^(2) sin pi (400 1 + 1)m`. Find (i) amplitude (ii) frequency (iii) wave length and (iv) velocity of the wave (W) velocity and acceleration of particle at `x=(1)/(6)m-at=0.1` a(vi) maximum particle velocity and accelerdion.
View SolutionThe amplitude of a wave disturbance propagating in the positive x-direction is given by at time in and by `v=(1)/(1+x^(2))` at time t=0 and by `y=(1)/([1+(x-1)^(2)])` at t=2 seconds, where x and y are in metres. The shape of the wave disturbance does not change during the propagation. What is the velocity of the wave?
View SolutionThe wave function of a pulse is given by y= `(3)/((2x+3t)^(2))` where x and y are in merre and t is in second
(i) Identify the direction of propagation.
(ii) Determine the wave velocity of the pulse.
View SolutionDoes the wave function `y=A_(0) cos^(-2)(2pi f_(0)t(2pi x)/(lambda_(0)))` represent a wve ?if yes. Then determine it's amplitude, frequency and wave-length .
View SolutionA transverse wave is travelling along as string from left to right, Fig. below represents the shape of the string at a given instant. Al this instant
(a) which points have an upward velocity?
(b) which points will have downward velocity ?
(c) which points have zero velocity ?
(d) which points have maximun magnitude of velocity
View SolutionA sinusoidal wave travelling in the positive direction on a stretched string has amplitude 2.0 cm, wavelength 1.0 m and wave velocity 5.0 m/s. Ar x = 0 and t = 0, it is given that `y=0 and (deltay)/(deltat)lt 0`. Find the dr wave function y(x, t).
View SolutionFigure shows a snaps hot of a sinusoidal travelling wave taken at t = 0.3s. The wavelength is 7.5 cm and the amplitude is 2 cm. If the crest P was at x = 0 at t=0), write the equation of travelling wave
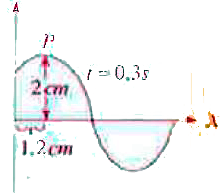
View SolutionThe displacement equation of a traveling wave pulse, moving along X axis is given by `y=(8)/((4+x^(2))^(2)) at t=0 and y=(8)/((x^(2)-10x+29))` What is the speed and direction of the prelse?
View SolutionCheck whether, the following equations can represent a progressive (travelling wave)
(a) `y=A cos(x^(3)-vt) (b) x=Ae^((vt-y))(c) y=A log((x)/(v)-t)`
View SolutionA wave travelling along a string is described by, y(x,t) = 0.005 sin ( 80.0x - 3.0 x). In which the numerical constants are in SI units ( 0.005m, 80.0 rad `m^(-1)` , and 3.0 rad `s^(-1)`) . Calculate (a) the amplitude , ( b) the wavelength , and (c ) the period and frequency of the wave. Also,calculate the displacement of the wave. Also, calaculate the displacement y of the wave at a distance x = 30.0 cm and time t =20s ?
View SolutionA metal wire of length 1 m has a mass of 33 g. Find the tension required to stretch the wire to propagate a transverse wave along its length, with a speed equal to 1/10 of the speed of sound in air at `0^(@)C`. (Velocity of sound in air at `0^(@) = 330 ms^(-1))`
View SolutionA copper wire is held at the two ends by rigid supports. At `30^(@)C` the wire is just tant, with negligible tension. Find the speed of transverse waves in this wire at `10^(@)C` if `Y=1.3xx10^(1!)N//m^(2), alpha=1.7xx10^(-5)l^(0)C and rho=9xx10^(3)kg//m^(3)`.
View SolutionA 4 kg block is suspended from the ceiling of an elevator through a string having a linear mass density of `19.2 xx 10^(-3) kg m^(-1)`. Find the speed with which a wave pulse can travel on the string if the elevator accelerates up at `2ms^(-2)(g=10 ms^(-2))`
View SolutionA uniform rope of length 12 m and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope ?
View SolutionA wave pulse starts propagating in +x-direction along a non-uniform wire of length L witdt mass per unit length given `mu=m_(0)+alpha x` and under tension of TN. Find the time taken by the pulse to travel from the lighter end (x = 0) to the heavier end.
View SolutionA thin string is held at one end and oscillaes vertically so that, y(x=0,0) = 8 sin dem Neglect the gravirational force. The string 's linear was density is 0.2 Kg/m and its tension is in the string passes through but filled with I kg : Due to frietion to the heat The heat transfer efficiency is 50%. Calentate how much time passes before the temperature of the bath rises by one degree kelvin.
View SolutionA reniform rope of mass 0.7 kg and length 2.45 in hangs from a ceiling (a) Find the speed of Transverse wave in the rope at a point 0.5m distrus from the lower end, b) Puste Calculate the time taken by a transverse wave to travel the full length of the rope `(g=9.8m//s^(2))`.
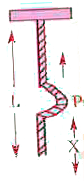
View SolutionBoth the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is `u_(1)` and in it is `v_(2)`. Then `v_(1)//v_(2)` is
View SolutionA steel wire 0.72 m long has a mass of `5.0 xx10^(_3) kg `.If the wire is under a tension of 60N , what is the speed of transverse waves on the wire?
View SolutionFind the speed of sound in a mixture of 1 mol of helium and 2 mole of oxygen at `27^(@)C`.
View SolutionA sound wave of amplitude of 3 cm starts towards right from origin and gets reflected at a rigid wall after a second. If the velocity of the wave is `340 ms^(-1)` and it has a wavelength of 2m, deduce the equations of the incident and reflected waves.
View SolutionThe displacement of a standing wave on a string is given by yox, 1) = 0.4 sin (0.5.x) cos (300) where Xandy are in centimeters.
(a) Find the frequency, amplitude and wave speed of the component waves.
(b) What is the particle velocity `x=2.4 cm ` at =0.8 s?
View SolutionThe vibrations of a string of length 60 cm fixed at both ends are represented by the equation. `y=4 sin [(pi x)/(15)] cos(96 pi t)` where x and y are in cm and t in sec.
(a) What is the maximum displacement al r = 5 cm?
(b) What are the nodes located along the string ?
(c) What is the velocity of the particle at `x=7.5 and t=0.25 s ?`
(d) Write down the equations of component waves whose superposition gives the above wave.
View SolutionA guitar string is 90 cm long and has a fundamental frequency of 124 Hz. Where should it be pressed to produce a fundamental frequency of 186 Hz?
View SolutionA wire having a linear mass density `5.0 xx 10^(-3) kg//m` is stretched between two rigid supports with a tension of 450 N. The wire resonates at a frequency of 420 Hz. The next higher frequency at which the same wire resonates is 490 Hz. Find the length of the wire.
View SolutionThe equation of a standing wave produced on a string fixed at both ends is `y=0.4 "sin"(pix)/(10) cos 600 pi t` where y' is measured in om 10 What could be the smallest length of string?
View SolutionThe equation for the vibration of a string fixed at both ends, vibrating in its its third harmonic is given by `y=0.4"sin" (pix)/(10) cos 600 pi t` where x and y are in cm
(1) What is the frequency of vibration ? (2) What are the positions of nodes?
(3) What is the length of string?
(4) What is the wavelength and speed of transverse waves that can interfer to give this vibration ?
View SolutionA wire has a length of 114 cm between two fixed ends. Where should two bridges be placed to divide the wire into three segments whose fundamental frequencies are in the ratio `1: 3:4 ?`
View SolutionA string 120 cm in length sustains a standing wave, with the points of string at which the displacement amplitude is equal to `sqrt(2` mm being separated by 5.0 cm, Find the maximum displacement amplitude. Also find the harmonic corresponding to this wave.
View SolutionA string fixed ar both ends hus consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm respeco rively,
(a) What is the minimum possible length of the string?
(b) If the tension is 10 N and the linear mass density is 4 g/m, what is the fundamental frequency?
View SolutionA wire of length 1m and mass 20g is stretched with a force of 800 N. Find the fundamental frequency. Also find the frequencies of the first two Overtones.
View SolutionA wire of uniform cross-section is stretched berween two points I w apart. The wire is fixed at one end und u weight of 9 kg is hung over a pulley at the other end produces fundamental frequency of 750 Hz.
(a) What is the velocity of transverse waves propagating in the wire ?
(b) If now the suspended weight is submerged in a liquid of density (5/9) that of the weight, what will be the velocity and frequency of the waves propagating along the wire ?
View SolutionThe length of the wire shown in figure between the pulleys is 1.5m and its mass is 12.0g. Find the frequency of vibration with which the wire vibrates in owo loops leaving the middle point of the wire between the pulleys at rest.
View SolutionAn aluminium wire of cross-sectional area 10"mis joined to a copper wire of the same crosssection. This compound wire is stretched from a fixed end, pulled by a load of 10 kg. The total length of the compound wire between two bridges is 1.5 m of which the aluminium wire is 0.6 m and the rest is the copper wire. Transverse vibrations are set in the wire by rising an external force of variable frequeney. Find the lowes! frequency of excitation for which standing waves are formed, such that the joint in the wire is anode. What is the total number of modes observed at this frequency excluding the two at the ends of the wire? The density of aluminium is `2.6xx10^(4) kg//m^(3)`.
View SolutionA wire of density `9 xx 10^(3) kg//m^(3)` is stretched between two clamps l m apart and is subjected to an extension of `4.9 xx 10^(-4) m`. What will be the lowest frequency of transverse vibrations in the wire ? `(Y=9xx10^(10)N//m^(2))`.
View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area `10^(-6)m^(2)` is rigidly fixed at both ends. The temperature of the wire is lowered by `20^(0)C`. If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration `[Y=2xx10^(11)N//m^(2) and alpha=1.21xx10^(-5)l^(0)C]`
View SolutionThird overtone of a closed organ pipe is in unison with fourth harmonic of an open organ pipe. Find the ratio of the lengths of the pipes.
View SolutionFor a certain orgas pipe, three succes ssive resonance frequencies are observed ol 425, 595 and 765 Hz respectively. Thking the speed of sound in air to be 340 m/s
(a) Explain whether the pipe is closed at one end or open at both ends
b) Determine the fundamental frequency and length of the pipe.
View SolutionA tube 1m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3 m long and has a mass of 0.01 kg. It is held fixed an both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration all its fundamental frequency by resonance Find the tension in the wire. Speed of sound in air: 330 m/s
View SolutionA tube of certain diameter and length 48 cm is open at both ends. Its fundamental frequency of resonance is found to be 320 Hz. The velocity of sound in air is 320 m/s. Estimate the diameter of the tube. One end of the tube is now closed. Calculate the fundamental resonance for the tube.
View SolutionAB is a cylinder of length I m fitted with a thin flexible diaphragm Cat middle and two other thin flexible diapharigms A and B at the ends. The portions AC and BC maintain hydrogen and oxygen gases respectively. The diaphragms A and B are set into vibrations of the same frequency. What is the minimum frequency of these vibrations for which diaphragm Cisa node? Under the conditions of the experiment velocity of sound in hydrogen is 1100 m/s and oxygen 300 m/s
View SolutionA source of frequency 340 Hz is kept above a vertical cylindrical tube closed at lower end. The length of the tube is 120 cm. Water is slowly poured in just enough to produce resonance. Then, the minimum height (velocity of sound = 340 m/s) of the water level in the tube for that resonance is
View SolutionA pipe of length 1.5m closed at one end is filled with a gas and it resonates in its fundamental with a tuning fork. Another pipe of the same length bur open at both ends is filled with air and it also resonates in its fundamental with the same tuning fork. Calculate the velocity of sound at `0^(@)C` in the gas. Given that the velocity of sound in air is 360 m/s at `30^(@)C` where the experiment is performed.
View SolutionA closed organ pipe of length 'L' and an open organ pipe contain gases of densities `rho(1) and rho_(2)` respectively . The compressibility of gases are equal in both the pipes . If the frequencies of their first overtones are same then, the length of the open organ pipe is
View SolutionAn open pipe in 2nd harmonic is in resonance with frequency/. Now one end of the tube is closed and frequency is increased to f, such that the resonance again occurs in nth harmonic, then find n and the relation between `f_(1),f_(2)`
View SolutionIf two sound waves, `y_1 = 0.3 sin 596 pi [t - x//330]` and `y_2 =0.5 sin 604 pi[t - x//330]` are superposed, what will be the (a) frequency of resultant wave (b) frequency at which the amplitude of resultant waves varies (c ) frequency at which beats aer produced. Find also the ratio of maximum and minimum intensities of beats.
View SolutionA tuning fork A produces 4 beats with tuningfork B of frequency 256 Hz. When A is filed beats are found to occur at shorter intervals. What was its original frequency?
View SolutionTwo identical sonometer wires have a fundamental frequency of 500 Hz when kept under the same tension. What fractional increase in the tension of one wire would cause an occurrence of 5 beats per sec, when both wires vibrate together?
View SolutionTwo open organ pipes 80 and 81 cm long found to give 26 beats in 10 sec, when each is sounding its fundamental note. Find the velocity of sound in air.
View SolutionA tuningfork 'A' produces 6 beats per second with another fork 'B'. On loading 'B' with a little wax, it produces 5 beats per second with 'A'. If the frequency of 'A'is 256 Hz find the frequency of 'B?.
View SolutionTwo sound waves of lengths 9 and 10 metres produce 34 beats in 9 seconds. Find the velocity of sound.
View SolutionThe frequency of a tuning fork A is 5% greater than that of a standard fork K. The frequency of another fork B is 3% less than that of K. When A and B are vibrated simultaneously 4 beats per second are heard. Find the frequencies of A and B.
View SolutionTwo forks A and B when sounded together produce 4 beat/s. The fork A is in unison with 30 cm length of a sonometer wire and B is in unison with 25 cm length of the same wire at the same tension Calculate the frequency of the forks.
View SolutionA stretched sonometer wire is in unison with a uning fork. When the length is increased by 2% the number of beats per second is 5. Find the frequency of the forks.
View SolutionA string under a tension of 129.6 N produces 10 beats per sec when it is vibrated along with a tuning fork. When the tension in the string is increased to 160 N, it sounds in unison with the same tuning fork, Calculate the fundamental frequency of the tuning fork.
View SolutionA metal wire of diameter 1 mm is held on two knife edges separated by a distance of 50 cm. The tension in the wire is 100 N. The wire vibrating with its fundamental frequency and a vibrating tuning fork together produce 5 beats per sec. The tension in the wire is then reduced to 81 N. When the two are excited, beats are heard again at the same rate. Calculate (a) the frequency of the fork and (b) the density of the material of the wire.
View SolutionThe fundamental frequeney of a sonumeter wire of length 'l' is `f_(0)` A bridge is now introduced at a distance of `Deltal` from the centre of the wire `(Deltal lt lt l)` . Find the number of beats heard if both sides of the bridge are set into vibration in their fundamental modes.
View SolutionThe lengths of two open organ pipes are l and `l+ Deltal, (Delta l lt lt l)` . If u is the speed of sound, find the frequency of beats between them.
View SolutionAn underwater swimmer sends a sound signal to the surface. If it produces 5 bears per second when compared with the fundamental tone of a pipe of 20 cm length closed at one end, what is the wavelength of sound in water? `("Take" v_("water")=1500 m//s and v_("air")= 360 m//s)`
View SolutionA column of air at `51^(@)C` and a tuning fork produce 4 beats per sec when sounded together. As the temperature of the air column is decreased, the number of beats per sec tends to decrease and when the temperature is `16^(@)C` the two produce 1 beat per see. Find the frequency of the tuning fork.
View SolutionA string 25 cm long and having a mass of 2.5g is under tension. A pipe closed at one end is 40 cm long. When the string is set vibrating in its firsy overtone and the air in the pipe in its fundamental frequency, 8 beats per sec are heard. It is observed that decreasing the tension in the string decreases the beat frequency. If the speed of sound in air is 320 m/s, find the tension in the string.
View SolutionA railway engine moving with a speed of 60 m/s passes in front of a stationary listener. The real frequency of the whistle is 400 Hz. Calculate the apparent frequency heard by the listener
(a) When the engine is approaching the listener
(b) When the engine is moving away from listener (V=340 m/s)
View SolutionA siren emitting a sound of frequency 1000 Hz moves away from you towards a cliff at a speed of 10 m/s. (a) What is the frequency of the sound you hear coming directly from the siren ? (b) What is the frequency of the sound you hear reflected off the cliff (c) What beat frequency would you hear ? Take the speed of sound in air as, 330 m/s.
View SolutionWhen a train is approaching the observer, the frequency of the whistle is 100 cps while when it has passed the observer, it is 50 cps. Calculate the frequency when the observer' moves with the trail.
View SolutionA whistle of frequency 540 Hz rotates in a circle of radius 2 m at a linear speed of 30 m/s. What is the lowest and highest frequency heard by an observer a long distance away at rest with respect to the centre of circle. Take speed of sound in air as 330 m/s. Can the apparent frequency be ever equal to actual?
View SolutionTwo tuning forks with natural freque. ncies 340 Hz each move relative to a stationary observer. One fork moves away from the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3 Hz. Find the speed of the tuning fork. (Velocity of sound in air = 340 in/s)
View SolutionA source of soud is moving along a circular orhit of dins 3 m with an angular velocity of 10 rad/s. sound detector located far away from the source is executing linear simple harmonic motion along the line BD with amplitude BC = CD = 6m. The frequency oscillation of the detector is `(5//pi)` rev/sec. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340 H, find the maximum and the minimum frequencies recorded by the detector velocity of sound :: 330 m/s)
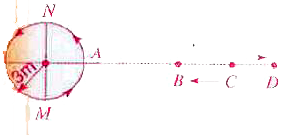
View SolutionA car approaching a crossing at a speed of 20 m/s sounds a horn of frequency 500Hz. when at 80m from the crossing, Speed of sound in air is 330 m/s. What freqnency is heard by an observer 60 m from the crossing on the straight road which crosses car road at right angles?
View SolutionA stretched wire under tension of 64 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of the sonometer wire has a length of 10 cm and mass lg. The vibrating tuning fork in now moved away from the vibrating wire at a constant speed and an observer standing near the sonometer hears one beat per sec. Calculate the speed with which the tuning fork is moved, if the speed of sound in air is 300 m/s.
View Solution
PROBLEM questions and complete solutions for chapter WAVES of JEE (MAIN AND ADVANCED) PHYSICS of Class 12
All Exercises from AAKASH SERIES Class 12 PHYSICS WAVES
- EXERCISE-IA (Matching )
- EXERCISE-IA (Statement type questions:)
- EXERCISE-IA (Theoretical questions :)
- EXERCISE-IB (Assertion (A) & Reason (R) Type Questions)
- EXERCISE-II (Beats : )
- EXERCISE-II (Doppler Effect : )
- EXERCISE-II (Pipes)
- EXERCISE-II (Strings (Speed of a travelling wave:))
- EXERCISE-II (Velocity of Sound:)
- EXERCISE-II (Wave Equations & Basics :)
- EXERCISE-III (Beats :)
- EXERCISE-III (Doppler effect :)
- EXERCISE-III (Pipes :)
- EXERCISE-III (Strings (Speed of travelling wave))
- EXERCISE-III (Velocity of Sound :)
- EXERCISE-III (Wave Equations & Basics)
- PROBLEM