Complete Solutions to Exercise-II of chapter ELECTRIC CHARGES AND FIELDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CHARGES AND FIELDS |
| AAKASH SERIES | Exercise-II |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
How many electrons must be removed from a piece of metal to give it a positive charge of `1.0 xx 10^(-7)C`
View SolutionA proton and an electron are placed 1.6cm apart in free space. Find the magnitude of electrostatic force between them. The nature of this force.
View SolutionTwo identical copper spheres are separated by 1m in vacuum. How many electrons would have to be removed from one sphere and added to the other so that they now attract each other with a force of 0.9N?
View SolutionThe force between two electrons when placed in air is equal to 0.5 times the weight of an electron. Find the distance between two electrons (mass of electron `= 9.1 xx 10^(-31)kg`)
View SolutionTwo charged particles having charge `2.0 xx 10^(-8)C`. Each are joined by an isolating string of length 1m and the system is kept on a smooth horizontal task. The tension in the string.
View SolutionTwo electrons separated by distance .r. experience a force F between them. The force between a proton and a singly ionized helium atom separated by distance 2r is
View SolutionTwo charges of equal magnitude and at a distance .r. exert a force F on each other. If the charges and halved and distance between them is doubled, then the new force acting on each charge is
View SolutionFour point charge of `+10^(-7)C, -10^(-7)C, -2 xx 10^(-7)C and +2 xx 10^(-7)C` are placed respectively at the corners A, B, C, D of a 0.05m square. Find the magnitude of the resultant force on the charge at D.
View SolutionTwo positive charges separated by a distance 2m each other with a force of 0.36N. If the combined charge is `26muC`, the charges are
View SolutionA Copper atom has 29 electrons revolving around the nucleus. A copper ball contains `4 xx 10^(23)` atoms. What fraction of the electrons be removed to give the ball a charge of `+9.6 mu C`?
View SolutionA pith ball of mass `9 xx 10^(-5)` kg carries a charge of `5muC`. What must be charge in another pith ball placed directly 2 cm above the given pith ball such that they held in equilibrium?
View SolutionN fundametal charges each of charge .q. are to be distributed as two point charges seperated by a fixed distance, then the maximum to minimum force bears a ratio (N is even and greater than 2)
View SolutionTwo point charages placed at a distance r. in the air experiene a certain force. Then the distance at which they will experience the same force in the medium of dielectric constant K is
View SolutionTwo charges 2 C and 6 C are separated by a finite distance. If a charge of-4 C is added to each of them,the initial force of `12 xx 10^(3)` N will change to
View SolutionTwo small balls having equal positive charge Q C on each are suspended by two insulating strings of equal length L metre, from a hook fixed to a stand. The whole setup is taken into space where there is no gravity (state of weightlessness). Then the angle `theta` between the two strings is
View SolutionThe force between two similar charges of magnitude 2C each separated by a distance 2km
View SolutionTwo charges `2muC and 1muC` are placed at a distance of 10cm. Where should a third charge be placed between them so that it does not experience any force.
View SolutionDeuteron and `alpha`-particle are put `1 A^(@)` apart in Air. Magnitude of intensity of electric field due to deuteron at `alpha`-particle is (N/C).
View SolutionTwo point charges Q and -3Q are placed at some distance apart. If the electric field at the location of Q is `vec (E )`, the field at the location of - 3Q is
View SolutionThe electric field at (30, 30) cm due to a charge of `-8nC` at the origin in `NC^(-1)` is
View SolutionTwo charges `4 xx 10^(-9)C and -16 xx 10^(-9)C` are separated by a distance 20cm in air. The position of the neutral point from the small charge is
View SolutionThe number of electrons to be put on a spherical conductor of radius 0.1m to produce an electric field of 0.036N/C just above its surface is
View SolutionThe magnitude of electric intensity at a distance .x. from a charge .q. is E. An identical charge is placed at a distance .2x. from it. Then the magnitude of the force it experience is
View SolutionThree small spheres each carrying a positive charge Q are placed on the circumference of a circle of radius to form an equilateral triangle. The electric field intenstiy at the centre of the circle will be.
View SolutionThe electric field in a region is radially out ward with magnitude E= Ar. Find the charge contained in a sphere of radius 20cm. Given `A= 100V m^(-2)`
View SolutionA sphere of mass 50gm is suspended by a string in an electric field of intensity `5NC^(-1)` acting vertically upward. If the tension in the string is 520 milli newton, the charge on the sphere is `(g = 10 ms^(-2))`
View SolutionA and B are two points separately by a distance 5cm. Two charges `10 mu C and 20mu C` are placed at A and B. The resultant electric intensity at a point P outside the charges at a distance 5cm from `10 mu C` is
View SolutionAt the corners A, B, C of a square ABCD, charges `10mC, -20 m C and 10mC` are placed. The electric intensity at the centre of the square to become zero, the charge to be placed at the corner D is
View SolutionA charged oil drop is suspended in uniform field of `3 xx 10^(4) V//m` so that it neither falls nor rises. The charge on the drop will be (take the mass of the charge `= 9.9 xx 10^(-15)kg "&" g= 10 m//s^(2)`)
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionA proton and an `alpha`-particle start from rest in a uniform electric field, then the ratio of times of flight to travel same distance in the field is
View SolutionIn a regular hexagon each corner is at a distance .r. from the centre. Identical charges of magnitude .Q. are placed at 5 corners. The field at the centre is `(K = (1)/(4pi in_(0)))`
View SolutionThe force experienced by a charge of `2mu C` in an electric field is `3 xx 10^(-3)N`. The intensity of the electric field.
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionIf `E_(a)` be the electric field strength of a short dipole at a point on its axial line and `E_(e )` that on the equatorial line at the same distance, then
View SolutionElectric charges q, q, -2q are placed at the corners of an equilateral triangle ABC of side 1. The magnitude of electric dipole moment of the system is
View SolutionAn electric dipole of moment p is placed with its centre at the origin along the x-axis. The electric field at a point P, whose position vector makes an angle `theta` with the x-axis, will make an angle…….. with the x-axis, when `tan alpha = (tan theta)//2`
View SolutionTwo charges `+3.2 xx 10^(-19)C and -3.2 xx 10^(-19)C` placed at `2.4A^(@)` apart form an electric dipole. It is placed in a uniform electric field of intensity `4 xx 10^(5)` volt/m. The electric dipole- moment is
View SolutionThe electric field due to an electric dipole at a distance from its centre position is E. If the dipole is rotated through an angle of `90^(@)` about its perpendicular aixs, electric field at the same point will be
View SolutionAn electric dipole is along a uniform electric field. If it is deflected by `60^(@)`, work done by agent is `2 xx 10^(-19)J`. Then the work done by an agent if it is deflected by `30^(@)` further is
View SolutionAn electric dipole made up of a positive and negative charge, each of `1mu C` separated by a distance of 2cm is placed in an electric field of `10^(5)N//C`, then the work done in rotating the dipole from the position of stable equilibrium through an angle of `180^(@)` is
View SolutionAn electric dipole s formed due to two particles fixed at the ends of a light rigid rod of length 1. The mass of each particle is m and charges are -q and +q The system is suspended by a torsionless thread in an electric field of intensity E such that the dipole axis is parallel to the filed if it is slightly displaced, the period of angular motion is
View SolutionAn electric dipole consists of two opposite charges of magnitude `1mu C` separated by a distance of 2cm. The dipole is placed in an electric field `10^(-5) Vm^(-1)`. The maximum torque does the field exert on the dipole is
View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive x-axis. The direction of electric field at point `(2, 2 sqrt2, 0)` is
View SolutionCalculate the net flux emerging from given enclosed surface `-Nm^(2) C^(-1)`

View SolutionThe electric field in a region of space is given by `E= 5i + 2j N//C`. The electric flux due to this field through an area `2m^(2)` lying in the Yz plane, in S.I. units, is
View SolutionA charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
View SolutionElectric field due to an infinite sheet of charge having surface charge density `sigma` is E. Electric field due to an infinite conducting sheet of same surface density of charge is
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density `sigma` is
View SolutionIf the electric flux entering and leaving an enclosed surface respectively is `phi_(1) and phi_(2)`, then electric charge inside the surface will be
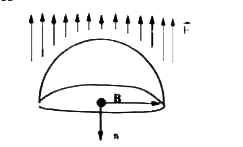
View SolutionIf a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is
View SolutionThe electric flux through a Gaussian surface that encloses three charges given by `q_(1) = -14nC, q_(2) = 78.85 nC, q_(3)= -56nC`
View SolutionAn infinitely long thin straight wire has uniform linear charge density of 1/3 coul `m^(-1)`. Then the magnitude of the electric intensity at a point 18cm away is
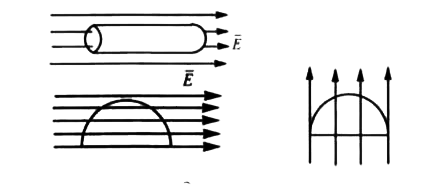
View SolutionIn a uniform electric field find the total flux associated with the given surfaces
View SolutionA charge q is placed at the centre of the open end of cylindrical vessel. Find the flux of the electric field through the surface of the vessel.
View SolutionThe electric field in a region of space is given by, `vec(E ) = E_(0) hat(i) + 2 E_(0) hat(j)` where `E_(0)= 100N//C`. The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly.
View Solution
Exercise-II questions and complete solutions for chapter ELECTRIC CHARGES AND FIELDS of JEE (MAIN AND ADVANCED) PHYSICS of Class 12