In a uniform electric field find the total flux associated with the given surfaces
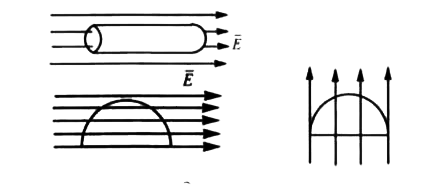
a−0,b−0,c−0
a−0,b−(πR2E),c−0
a−2πRE,b−(πR2E),c−0
a−πR2E,b−0,c−0
The correct Answer is:A
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Exercise
Explore 57 Videos
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Exercise-I
Explore 80 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 44 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 32 Videos
Similar Questions
Knowledge Check
Surface subtends a solid angle of π on a point charge +q. Electric flux due to point charge, associated with the given surface, is
Aq/ε0Bq/2ε0Cq/4ε0Dq/8ε0Find the total flux due to charge q associated with the given hemispherical surface
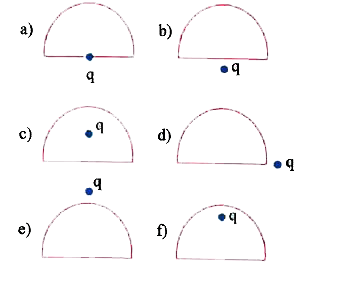 A(a)q2ε0,(b)0,(c)qε0,(d)0,(e)0(f)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0(f)qε0C(a)q2ε0,(b)qε0,(c)0,(d)qε0,(e)0(f)qε0D(a)0,(b)q2ε0,(c)0(d)qε0,(e)qε0(f)qε0
A(a)q2ε0,(b)0,(c)qε0,(d)0,(e)0(f)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0(f)qε0C(a)q2ε0,(b)qε0,(c)0,(d)qε0,(e)0(f)qε0D(a)0,(b)q2ε0,(c)0(d)qε0,(e)qε0(f)qε0Find the total flux due to charge qassociated with the given hemisphercal surface
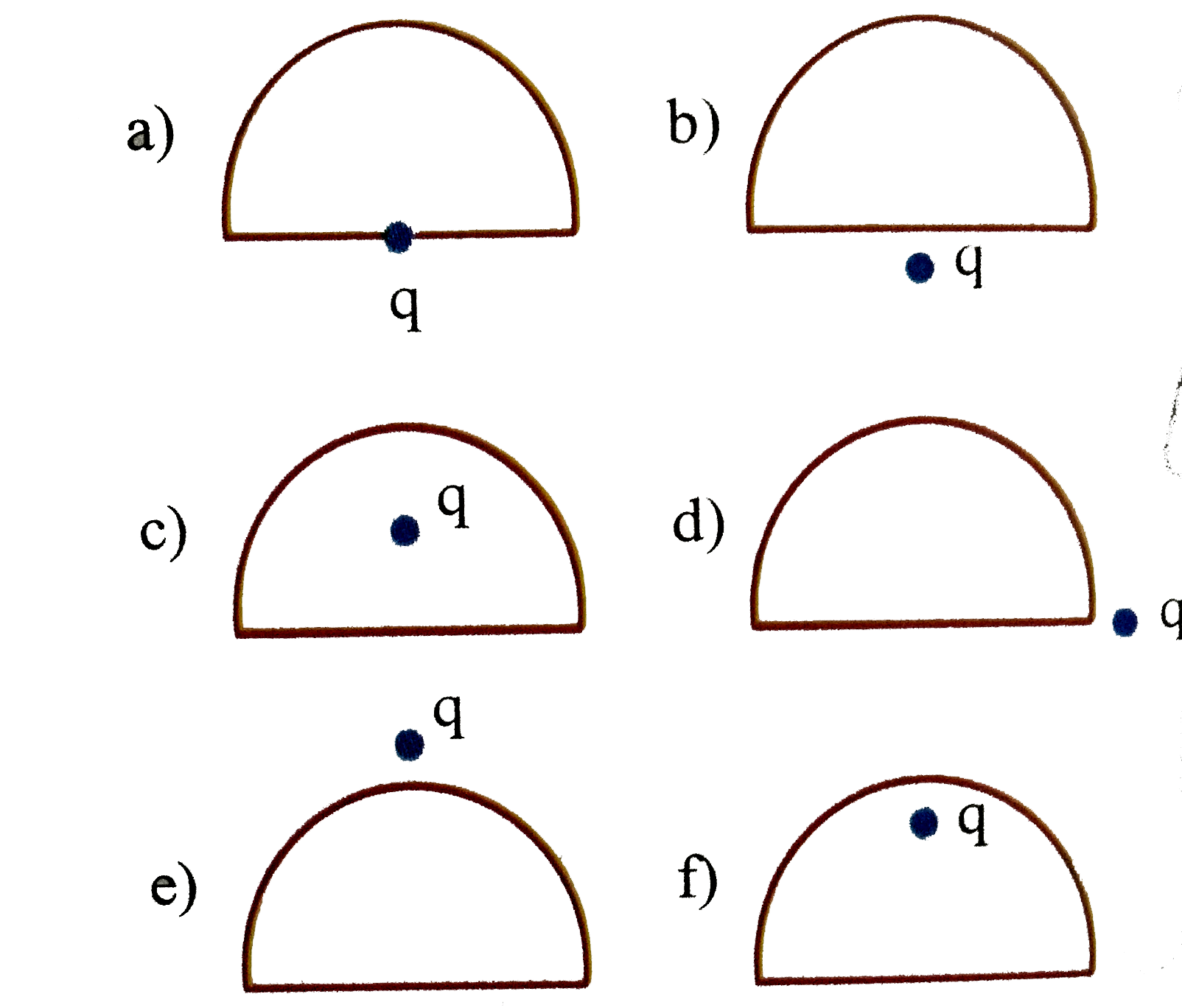 Aq2ε0,(b)0,(c)qε0,(d)0,(e)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0C(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0D(a)0,(b)q2ε0,(c)0,(d)qε0,(e)qε0(f)qε0
Aq2ε0,(b)0,(c)qε0,(d)0,(e)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0C(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0D(a)0,(b)q2ε0,(c)0,(d)qε0,(e)qε0(f)qε0
Find the total flux due to charge q associated with the given hemispherical surface
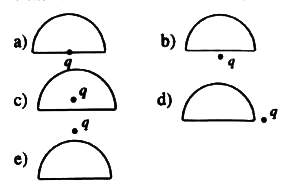
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View Solutionin the given figure a cone lies in a uniform electric field E the electric flux entering the cone is

View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View Solution


