Complete Solutions to PRACTICE EXERCISE of chapter COMPLEX NUMBERS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMPLEX NUMBERS |
| AAKASH SERIES | PRACTICE EXERCISE |
| Number Of Questions | 93 |
| Academic Year | 2023-24 |
The value of `sum_(n= 1)^(13) (i^(n) + i^(n + 1))` , where `i=sqrt(-1)` is
View Solution`1 + i^(2) + i^(4) + i^(6) + … +i^(2n)` =
View SolutionIf `((1 + i)/(1- i))^(x) = 1` then
View SolutionThe value of `((1 + i)^(2n + 1))/((1- i)^(2n -1)) = `
View SolutionThe value of `(1 + i)^(6) + (1 - i)^(6)` is
View SolutionIf `u + iv = (3i)/(x + iy + 2)` , then y in terms of u , v is
View SolutionIf `(x + 3i)/(2 + iy) = 1 - i` then the value of `(5x - 7y)^(2) =`
View SolutionIf `x + iy = (1)/((1 + cos theta + isin theta))` then `sin^(-1) x = `
View SolutionThe real value of `theta` for which the expression `(1 -isin theta)/(1 + 2 isin theta)` is a real number is
View SolutionFind the values of the following :
` ( sqrt3/2 + i/2)^(5) - ( sqrt3/2 - i/2)^(5)`
View SolutionIf `x = (-5 + isqrt3)/(2)` then `(x^(2) + 5x)^(2) + x ( x+ 5) = `
View SolutionIf `z = 3- 5i` then `z^(2) - 10z + 30=
View SolutionIf `theta` is real then the modulus of `(1)/(1 + cos theta + isin theta) ` is
View SolutionIf `(x + iy)^((1)/(3)) = 5+ 3i` , then 3x + 5y =
View SolutionIf `alpha` is a non-real root of `x^(7) = 1` then `alpha(1 + alpha) (1 + alpha^(2) + alpha^(4)) =`
View SolutionExpress `(3- 2i)/(5 + 4i) + (3 + 2i)/(5 - 4i)` in the form of a + ib
View SolutionThe conjugate of `(2 + 3i)/(1 + 2i)` is
View SolutionIf `(2 - i)/((1 - 2i)^(2))` and `(-(x + 11i))/(25)` are conjugate complex numbers , then x =
View SolutionThe modulus of `((3 + i) (2 - i))/(1 +i)` is
View SolutionIf `x -iy = sqrt([(a - ib)/(c-id)])` , then `(x^(2) + y^(2))^(2) =`
View SolutionIf `m_1,m_2,m_3 and m_4` respectively denote the moduli of the complex numbers `1+4i,3+I,1-I and 2 -3i` , then the correct one , among the following is
View SolutionThe mod-amplitude form of `-sqrt3 - i`
View SolutionThe mod-amplitude form of `sin theta + icos theta` is
View SolutionIf `(pi)/(2) lt alpha (3pi)/(2) , the modulus argument form of `(1 + cos 2 alpha) + isin 2 alpha` is
View SolutionIf `(pi)/(5)` and `(pi)/(3)` are respectively the arguments of `barz_(1)` and `z_(2)` , then the value of Arg `(z_(1)- z_(2))` is
View SolutionIf Arg (3z-2i) = pi//2 then the locus of z = x +iy is
View SolutionThe argument of `((1 - isqrt3))/((1+isqrt3))` is equal to
View SolutionGiven `|z| = 14` and amp `z = (7pi)/(6)` , then z is =
View SolutionIf `(sqrt3 + i) = (a + ib) (c + id)` then `tan^(-1) (b)/(a) + tan^(-1) (d)/(c) =`
View SolutionLet z,w be complex number such that `barz+ibarw=0` and arg zw `=pi` . Then arg z =
View SolutionIf Arg `((z+1)/(z-1))=pi/6` then the locus of z = x + iy is
View SolutionIf `|z| = 1` and arg `[z^(2) + barz] = x` arg z then x
View SolutionIf `z = x + iy` and if the point P in the Argand plane represents z , then the locus of P satisfying the equation `|z- 3i| + |z + 3i| = 10` is
View SolutionIf |z-3+i| = 4 then the locus of z = x +iy is
View SolutionIf `|(z-1)/(z-3)|` = 2 then the locus of z = x +iy is
View SolutionThe locus of the point z = x +iy satisfying the equation `|(z-1)/(z+1)|=1` is given n=by
View SolutionThe equation of the locus of 2 such that `|(z-i)/(z+i)|=2`, where z = x + iy is a complex number , is
View SolutionThe locus of the point z in the argrand plane for which `|z+1|^2+|z-1|^2=4` is a
View SolutionIf `|z+i|^2-|z-i|^2=3` then the locus of z is
View SolutionThe points representing the complex numbers z for which `|z+4|^2-|z-4|^2 = 8` lie on
View SolutionIf `(2z_(1))/(3z_(2))` is purely , an imaginary number , then `|(z_(1) - z_(2))/(z_(1) + z_(2))|` is equal to
View SolutionIf `|z_(1) | = |z_(2)| = 1` , then `|z_(1) + z_(2)| =`
View SolutionThe modulus of `sqrt2i-sqrt(-2i)` is
View SolutionIf |z-1| = 2 then the locus of z is
View SolutionIf `|z + 1| = sqrt2 | z- 1|` and z is a complex number , then the locus of z is
View SolutionIf the complex numbers `z_(1) , z_(2) , z_(3)` represents the vertices of an equilateral triangle such that `|z_1| = |z_2| = |z_3|` then
View SolutionIf `z = 2e^(i"" (pi)/(4))` then `|e^(iz)|` =
View SolutionIf `|z + barz| + |z - barz|` , then the locus of z is
View SolutionIf `|z + 4| + |z - 4| = 10` represents an ellipse then length of its minor axis is
View SolutionThe region represented by `|z+a|+|z-a| lt4a` is
View Solution`|z-4|lt|z-2|` represents the region given by
View SolutionFor any two complex numbers `z_(1)` & `z_(2)` and any two real numbers `a , b |az_(1) - bz_(2)|^(2) + |bz_(1) + az_(2)|^(2) =`
View Solution`sqrt(-5+12i)=`
View Solution`sqrti` =
View SolutionThe value of `sqrt(x^(2) + 2ix- 1)` is
View SolutionIf n is an integer and not a multiple of 3 then `omega^(n) + omega^(2n) = `
View Solution`(3 + 5 omega + 3omega^(2))^(6) =`
View Solution`(1+omega)(1+omega^(2))(1+omega^(5))..........2n` factors =
View Solution`(1- omega + omega^(2))^(7) + (1 + omega - omega^(2))^(7) = `
View Solution`(1-omega+omega^(2))(1-omega^(2)+omega^(4))(1-omega^(4)+omega^(8))(1-omega^(8)+omega^(16))`
View SolutionIf ` 1 , omega , omega^(2)` are the cube roots of unity , then find the values of the following .
`(a + 2 b)^(2) + ( a omega^(2) + 2 b omega)^(2) + ( a omega + 2 b omega^(2))^(2)`
View SolutionIf ` 1 , omega , omega^(2)` are the cube roots of unity , then the roots of `(x - 2)^(2) + 1 = 0` are
View SolutionIf `1 , omega , omega^(2)` are the cube roots of unity, then prove that
`(2 - omega)(2 -omega^(2)) (2 - omega^(10)) ( 2 - omega^(11)) = 49`.
View SolutionThe value of `((- 1 + isqrt3)/(2))^(100) + ((- 1 - isqrt3)/(2))^(100)` is equal to
View SolutionIf x = a + b , y = `a omega^(2) +b omega` and `z = a omega + b omega^(2)` , then `x^(2) + y^(2) + z^(2)` is equal to
View SolutionIf `alpha , beta` are the imaginary cube roots of unity then `alpha^(4) + beta^(4) - (alpha + beta)^(4) `=
View SolutionIf ` 1 , omega , omega^(2)` are the cube roots of unity , then `(a+ b)^(3) + (a omega + b omega^(2))^(3) + ( a omega^(2) + b omega)^(3) = `
View SolutionThe value of `((-1 + isqrt3)/(2))^(36) + ( (-1 - isqrt3)/(2))^(36) =`
View SolutionThe solution of the equation `|z| - z =1 + 2i` is
View SolutionIf `(1 + isqrt2)^(x) = 3^(x)` , then its only integral solution is
View SolutionIf `barz = iz^(2)` then the number of values of z is
View SolutionThe number of solutions of `z + sqrt2 (| z+ 1|) + i=0`
View SolutionIf the complex number z lies on `|z| = 1` then `(2)/(z)` lies on
View SolutionIf `zbarz=4` then the locus of z is
View SolutionMatch the items of List - I with those of List-II
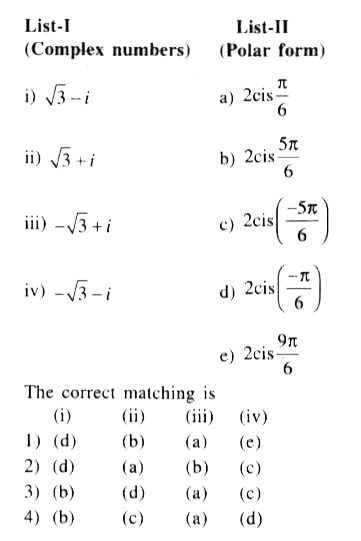
View SolutionIf z = x +iy and P represents z in the Argand plane and mod (2z-3) = 4 , then the locus of P is
View SolutionIf `z = (lambda + 3) + isqrt( 5 - lambda^(2))` , then the locus of z is a circle with centre at
View SolutionIf `z=(x+iy)` and if the point P in the Argarand plane represent z, then desrcibe geo-metrically the locus of P satispfying the equation.
`|z|^(2) 4 Re (z+2)`
View SolutionIf `z_1=1+2i,z_2=2+3i,z_3=3+4i, " then " z_1,z_2and z_3` represents the vertices of
View SolutionIf z is a complex number with `|z|ge 5` . Then the least value of `|z +(2)/(z)|` is
View Solution`(1 + x)^(n) = p_(0) + p_(1) x + p_(2) x^(2) + … + p_(n) x^(n) ` , then `p_(0) + p_(3) + p_(6) + …..` =
View SolutionThe cube roots of unity when represented on the Argand diagram form the vertices of an
View SolutionIf `a , b , c in R ` such that `a + b + c= 0` and `az_(1) + bz_(2) + cz_(3) = 0` then `z_(1) , z_(2) , z_(3)` are
View SolutionIn the Argand plane the area in square units of the triangle formed by the points `1 +i, 1- i, 2i` is
View SolutionIf the area of the triangle on the complex plane formed by the point z, iz and z +iz is 50 square units , then |z| is
View SolutionIf `|z-2/z|=2` then the greatest value of |z| is
View SolutionIf `|z| ge 3` , then the least value of `|z + (1)/(z)|` is
View SolutionThe value of `(i)^(i)` is
View Solution`Log_(e) ((1 + i)/(1- i))= `
View SolutionThe real and imaginary points of log `(1 + isqrt3)` are
View SolutionAssertion (A) : If 3 + iy is a root of `x^(2) + ax + b = 0` then a = -6
Reason (R) : If a, b , c are real and `Delta lt 0` the roots of `ax^(2) + bx + c = 0` are conjugate complex numbers
View SolutionIf `log_((1)/(sqrt(3))){(|z|^(2)-|z|+1)/(2+|z|)}gt -2` , then z lies inside
View SolutionIf `omega` is a complex cube root of unity , then for any `n gt 1 underset(r = 1)overset(n - 1) sumr(r + 1 - omega)(r + 1 - omega^(2) ]=`
View Solution
PRACTICE EXERCISE questions and complete solutions for chapter COMPLEX NUMBERS of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12