Complete Solutions to EXERCISE - I of chapter COMPLEX NUMBERS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COMPLEX NUMBERS |
| AAKASH SERIES | EXERCISE - I |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
`sqrt5 sqrt(-125)=`
View SolutionIf `i= sqrt-1` and n is a positive integer , then `i^(n) + i^(n + 1) + i^(n + 2) + i^(n + 3)` is equal to
View SolutionThe least positive integer n for which `(1+i)^n/((1-i))^(n-2) ` is a real number is
View Solution`(1 +i)^(6) + (1 - i)^(3) = `
View SolutionThe multiplicative inverse of `((3 + 4i))/(25)` is
View SolutionThe additive inverse of `(1 + 2i) (3 - 4i)` is
View Solution`sum_(n = 0)^(oo) ((2i)/(3))^n` =
View Solution`((2+3i)/(2-3i))-((2-3i)/(2+3i))` in the form of a + ib
View SolutionThe conjugate complex number of `(2-i)/((1-2i)^2)` is
View SolutionThe complex number `sinx+icos 2x and cosx-isin2x` are conjugate to each other for
View SolutionThe modulus of `(sqrt3 + i)/((1 + i) (1 + sqrt3i))` is
View SolutionIf `alphaand beta` are real them `|(alpha+i beta)/(beta+ialpha)|=`
View SolutionIf `(sqrt(3)i)^(100)=2^(99)(a+ib)`. Then shot that `a^(2)+b^(2)=4`
View SolutionIf `alpha_1,alpha_2,alpha_3` respectively denote the moduli of the complex number `-i,1/3(1+i) and -1 +i` , then their increasing order is
View SolutionIf `(pi)/(2)` and `(pi)/(4)` are the arguments of `z_(1)` and `barz_(2)` respectively , then Arg `(z_(1))/(z_(2))` =
View SolutionIf `z_(1)=-1,z_(2)=i` then find Arg `((z_(1))/(z_(2)))`
View SolutionThe mod-amplitude form of `-sqrt3 - i`
View Solution`z=1+isqrt(3)rArr|Arg z|+|Argbarz|=`
View Solution`sqrt(-8 - 6i)` is equal to
View SolutionThe value of `sqrt(15 + 8i) + sqrt(15 - 8i)` is equal to
View SolutionIf n is a multiple of 3 then `omega^(n) + omega^(2n) = `
View Solution` (1 + omega) (1 + omega^(2)) (1 + omega^(3)) (1 + omega^(4)) (1 + omega^(5)) (1 + omega^(6)) …. (1 + omega^(3n)) = `
View SolutionIf ` 1, omega , omega^(2)` are the cube roots of unity, then prove that `1/(2 + omega) - 1/(1 + 2 omega) = 1/( 1 + omega)` .
View SolutionThe value of `((- 1 + sqrt-3)/(2))^(26) + ((- 1 - sqrt-3)/(2))^(26)` is equal to
View SolutionIf `(1 + omega)^(7) = A + B omega` then (A , B) =
View SolutionIf |3z-2|=5 then the locus of z is
View SolutionIf `|z -2 - 3i| = 5` then the locus of `z = x +iy` is
View SolutionThe equation `|z-1|^(2) + |z+1|^(2) = 2` represents
View SolutionIf Re `(z^2)=2` then the locus of z is
View SolutionIf amp (z-i) `=pi//3` then the locus of z is
View SolutionThe locus of Z satisfying `|z| + |z - 1| = 3` is
View SolutionIf the amplitude of `z - 2 - 3i " is " pi//4` , then the locus of z = x +iy is
View SolutionThe complex number `(1 + 2i)/(1 - i)` lies in the
View SolutionIf three complex number are in A.P then they lie on
View SolutionIn the Argand plane, the points represented by the complex numbers `2-6i ,4-7i, 3 - 5i and 1 - 4i` form
View SolutionThe condition for the points `z_(1) , z_(2) , z_(3) , z_(4)` taken in order in the Argand plane to be the vertices of the parallelogram is
View SolutionThe equation of the line joining the points represented by 2- 3i and -3+ 4i in the Argand plane is
View SolutionThe number of complex number z such |z-1|=|z+1|=|z-i| equals
View SolutionStatement - I : If `z_(1)` and `z_(2)` are two nonzero complex numbers such that `|z_(1) + z_(2) | = |z_(1)| + |z_(2)|` then arg `z_(1)` - arg `z_(2)` is `pi//2`
Statement - II : `z_(1)` and `z_(2)` are two complex numbers such that `|z_(1) z_(2)| = 1` and arg `z_(1) ` - arg `z_(2)` is `pi//2` then `barz_(1) z_(2) = -i`
View SolutionStatement - I : If a and b are positive real numbers then `sqrt(-a) xx sqrt(-b)` is equal to `sqrt(ab)`
Statement - II : The argument of `(1 + isqrt3)/(1 -isqrt3)` is `120^(0)`
View SolutionStatement - I : If `z = barz` then z is purely imaginary
Statement- II : If `z = -barz` then z is purely real
View SolutionIn Argand plane , the quadrant in which `(1 + 2i)/(1 -i)` lies is
View SolutionThe descending order of the moduli of
`z_(1) = (3 - 4i) (4 + 3i) , z_(2) = (3 + 4i)/(1 +i) , z_(3) = ((3 + i) (2- i))/(1+ i) , z_(4) = 5 + 12 i` is
View SolutionMatch the following:
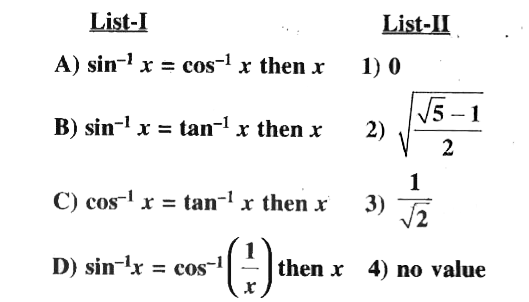
View Solution`(3 - omega) ( 3- omega^(2)) ( 3- omega^(4)) (3 - omega^(8))` =
View Solution`i+ i^(2) + i^(3) + i^(4) + …. + i^(100)`
View Solution`1 + omega + omega^(2) + ….. + omega^(300)`
View Solution`i+ 2i^(2) + 3i^(3) + 4i^(4) + …. + 100i^(100)` =
View Solution`omega + 2omega^(2) + 3 omega^(3) + ….. 90 omega^(90) = `
View Solution
EXERCISE - I questions and complete solutions for chapter COMPLEX NUMBERS of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12