Complete Solutions to PRACTICE EXERCISE of chapter QUADRATIC EQUATIONS & EXPRESSIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | QUADRATIC EQUATIONS & EXPRESSIONS |
| AAKASH SERIES | PRACTICE EXERCISE |
| Number Of Questions | 88 |
| Academic Year | 2023-24 |
If `(3x+2)/(2x+3)=(4x+3)/(3x+4)`, then x =
View SolutionThe roots of the equation `(b-c) x^2 +(c-a)x+(a-b)=0`are
View SolutionA root of the equation `(x-2)(x-3)=(155 xx 78)/((77)^(2))`
View SolutionA root of the equation `(a+c)/(x+a)+(b+c)/(x+b)=(2(a+b+c))/(x+a+b)` is
View SolutionIf `(x-a+2b)^(2)+(x-2a+b)^(2)=(a+b)^(2)`, then one value of x is
View SolutionIf `alpha, beta` are the rootsof `6x^(2)-4sqrt2 x-3=0`, then `alpha^(2)beta+alpha beta^(2)` is
View SolutionAssertion (A): If `alpha, beta` are the roots of `x^(2)-x+1=0`, then `alpha^(5)+beta^(5)=1`
Reason (R) : The roots of `x^(2)-x+1=0` are `omega,omega^(2)`.
View SolutionIf ` alpha , beta ` are the roots of ` ax ^2 + bx +c=0` then `alpha ^5 beta ^8 + alpha beta ^5=`
View SolutionIf w, `w^(2)` are the roots of `x^(2)+x+1=0` and `alpha, beta` are the roots of `x^(2)+px+q=0` then `(w alpha+w^(2)beta)(w^(2)alpha+w beta)` =
View SolutionIf the roots `ax^(2)+bx+c=0` are `(3)/(2),(4)/(3)` then `(a+b+c)^(2)` =
View SolutionIf a, b are the roots of `x^(2)+x+1=0`, then `a^(2)+b^(2)` is
View SolutionIf `alpha, beta` are the roots of `x^(2)+x+1=0`, then `alpha^(-2)+beta^(-2)` is
View SolutionIf `alpha, beta` are the roots of `ax^(2)+bx+c=0`, `alpha beta=3` and a, b, c are in A.P., then `alpha+beta` =
View SolutionIf `alpha, beta` are the roots of `x^(2)+ax+12=0` such that `alpha-beta=1`, then a =
View SolutionThe values of P for which the difference between the roots of the equation `x^(2)-px+10=0` is 3 are
View SolutionIF the different between the roots of ` x^(2) -px+q=0` is 2, then the relation between p , and q is
View SolutionIf x-2 is a factor of `x^(2)+6x+16b`, then b =
View SolutionIf the sum of the roots of `kx^(2) + 2x + 3k = 0` is equal to their product, then k =
View SolutionIf the sum of the roots of `x^(2) + bx + 1 = 0`, is equal to the sum of their squares, then b =
View SolutionIF `alpha , beta ` are the roots of `ax^2 + bx +c=0` then the equation whose roots are `2 + alpha ,2+beta ` is
View SolutionIf `alpha, beta` are the roots of `x^(2)+x+1=0`, then the equation whose roots are `alpha^(2), beta^(2)` is
View SolutionIF ` alpha, beta ` are the roots of `9x^2+6x+1=0` then the equation with the roots `1// alpha , 1//beta ` is
View SolutionThe equation whose roots are double the roots of the equation `x^(2) + 6x + 3 = 0` is
View SolutionThe equation formed by increasing each roots of `2x^(2) - 3x - 1 = 0` by 2 is
View SolutionIf one root of `x^2+kx +12 =0` may be the triple the other , then k=
View SolutionLet `alpha` and `beta` be the roots of the quadratic equation `ax^(2) + bx + c = 0`, observe the lists given below :
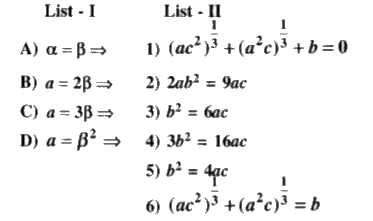 The correct match is
The correct match is
View SolutionIf one root of the equation `x^(2) + px + q = 0` is the square of the other, then `p^(3) + q^(3)` =
View SolutionIf `alpha+beta=3` and `a^(3)+beta^(3) = 7`, then `alpha` and `beta` are the roots of the equation
View SolutionThe equation whose roots are smaller by 1 then those of `2x ^2-5x +6=0` is
View SolutionAssertion (A): The roots of the equation `2x^(2) - 15x + 4 = 0` are each increased by 3, then the new equation is `2x^(2)-27x + 67 = 0`
Reason (R): The equation whose roots are increased by k then those of f(x) = 0 is `f(x//k) = 0`
View SolutionThe equation formed by decreasing each root of `ax^(2) + bx + c = 0` by 2 is `x^(2) + 4x +3= 0` then
View SolutionIf `alpha, beta` are the roots of `x^(2)+3x+1=0`, then the equation whose roots `2-alpha, 2-beta` is
View SolutionIf `alpha, beta` are the roots of `2x^(2) + 5x + 2 = 0`, then the equation with roots `(1)/(alpha+1), (1)/(beta+1)` is
View SolutionThe number of integral solutions of `2(x^(2)+(1)/(x^(2)))-7(x+(1)/(x)) +9=0` when `x != 0` is
View SolutionIF ` 3+i` is a root of the equation ` x^2 + ax + b=0` then a=
View SolutionThe roots of the equation `x^(2)-2ax+8a-15=0` are equal, then a =
View SolutionIf one root of the equation ` I x ^2 - 2(1+i) x+ (2-i) =0` is 2- I then the root is
View SolutionIf x = 1 + i is a root of the equation `x^(2) - ix - 1-i = 0` then the other real root is
View SolutionAssertion (A) : If the roots of `(b-c) x^(2) + (c-a) x+(a-b) = 0` are equal then a, b, c are in A.P.
Reason (R): If in `ax^(2) + bx + c = 0`, sum of the coefficients is equal to zero then c = a
View SolutionIf `x^(2) - (5m - 2)x + 4m^(2) + 10m + 25` is a perfect square then m = The roots of the equation `x^(2)+2ax+a^(2)+b^(2)=0` are
View SolutionThe roots of the equation `x^(2)+2ax+a^(2)+b^(2)=0` are
View SolutionThe roots of the equation `2(a ^2 +b^2)x^2+2(a+b)x+1=0` are
View SolutionFor p, `q in R`, the roots of `(p^(2) + 2)x^(2) + 2x(p +q) - 2 = 0` are
View SolutionIf the equation `x^(2)-x+ m^(2) = 0` has no real roots then m can satisfy
View SolutionIf the roots `(1)/(x+k+1)+(2)/(x+k+2)=1` are equal in magnitude but opposite in sign, then k =
View SolutionThe roots of the equation `5x^(2)+10x-7=0` are
View SolutionThe set of values of p for which the roots of the equation `3x^(2) + 2x + p(p-1) = 0` are of opposite signs is
View SolutionIf the roots of `ax^(2)+ bx + c = 0` are equal in magnitude but opposite in sign, then
View SolutionIf the roots of `ax^(2) + bx + c = 0` are both positive and `b lt 0`, then
View SolutionThe value of 'a' for which the quadratic equation `2x^(2) - x(a^(2) + 8a -1) + a^(2) - 4a = 0` has roots with opposite signs, lie in the interval
View SolutionLet `alpha`, `beta` be the roots of the equation `(x - a)(x - b) = c`, `c != 0`, then the roots of the equation `(x-alpha)(x-beta)+c= 0` are
View SolutionThe equation `|x|^(2) -|x|-6 = 0` has
View SolutionIf `|x^(2)|-3|x|+2=0` then x =
View SolutionSolutions of the equation x|x+1|+1=0 are
View SolutionIf m is a positive integer then the solutions of `x^((2)/(5))-5x^((1)/(m))+4=0` are
View SolutionIf the sum of the roots of `ax^(2) + bx + c = 0` is equal to the sum of the reciprocals of their squares then `bc^(2), ca^(2), ab^(2)` are in
View SolutionIf `a != 0`, then the equation `(x-a-1)/(x-a)=(a+1)-(1)/(x-a)` has
View SolutionThe number of real solutions of the equation `((9)/(x))^(x)= -3+x-x^(2)` is
View SolutionSolve `x^(2//3)+x^(1//3)-2=0`
View SolutionIf the equations `x^(2)-ax+bc=0` and `x^(2)+bx+ca=0` have a common root, then a + b + c =
View SolutionIf the equation `x^(2)+ax+b=0` and `x^(2)+bx+a=0` have a common root, then their other roots satisfy the equation
View SolutionSuppose the that quadratic equations `ax^(2)+bx+c=0 and bx^(2)+cx+a=0` have a common root. Then show that `a^(3)+b^(3)+c^(3)=3abc`.
View SolutionIF ` x^2 +bx +a=0, ax^2+x+b=0` have a common root and the first equation has equal roots then ` 2a^2+b=`
View SolutionIf the quadratic equation `ax^(2) + 2cx + b = 0` and `ax^(2) + 2x + c = 0` (`b != c`) have a common root then a + 4b + 4c is equal to
View Solutionthe expression ` 2x ^2 + 4x +7` has minimum value m at `x= alpha ` . The ordered pair `( alpha , m) ` is
View SolutionThe maximum value of the expression `(x^(2)+x+1)/(2x^(2)-x+1)`, for `x in R`, is
View SolutionA = The maximum value of `4x^(2) + 4x + 5`
B = The maximum value of `8x-x^(2)`
C = The maximum value of `-x^(2) + 4x-4`
D = The maximum value of `-7x^(2) + 100` then
View SolutionThe range of `(x^(2)-x+1)/(x^(2)+x+1)` is
View SolutionOut of the two roots of `x^(2)-2 lambda x + lambda^(2)-1= 0`, one is greater than 4 and the other root is less than 4, then the limits of `lambda` are
View SolutionAssertion (A): The roots of `ax^(2) + bx + c = 0`, where `a != 0`, b, `c in R` are non-real complex and `a + c lt b`. Then `4a + c lt 2b`
Reason (R): If the quadratic equation `ax^(2) + bx + c = 0` has imaginary roots then `AAx in R` `ax^(2) + bx + c` have same sign
View SolutionIf x `in` R, then the range of `(x)/(x^(2)-5x + 9)` is
View SolutionIf `4 lt x lt 8` then the value of `12x -x^(2) - 32` is
View SolutionThe greatest positive integral value of x for which 200 - x(10 + x) is positive is
View SolutionThe range of values of x which satisfy `2x^(2) + 9x + 4 lt 0` and `x^(2) - 5x + 6 lt 0` is
View SolutionIf `x^(2) + 6x-27 gt 0, -x^(2) + 3x + 4 lt 0`, then x lies in the interval
View SolutionIf `4x^(2) + kx + 3 ge 0` for all real values of x then k lies in the interval
View SolutionThe greatest negative integer satisfying `x^(2) - 4x - 77 lt 0` and `x^(2) gt 4` is
View SolutionIF the inequation ` sqrt(3x -8) lt -2 ` then
View SolutionThe range of values of x for which the inequality `(x-1)/(4x+5) lt (x-3)/(4x-3)` holds is
View SolutionIf `sqrt(2x - 4) le 2 - x`, then the range of x is
View SolutionThe integer k for which the inequality `x^(2) - 2 (4k - 1)x + 15k^(2) - 2k -7 gt 0` is valid for any x, is
View SolutionIf `x^(2)- y^(2) + 4x-6y + k` is resolvable into two linear factors, then k =
View SolutionIf ` x^2 + 4y ^2 - 8x +12 =0` is satified by real values of x nad y then y must lies between
View SolutionThe quadratic equation `ax^(2) + bx + c = 0` has two roots then match the following lists.
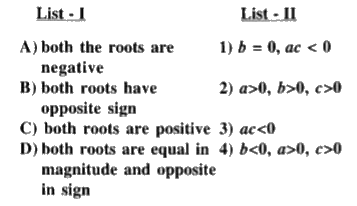
Find the correct match from List-I to List-II.
View SolutionIf a and b are the non-zero roots of the equation `x^(2) + ax + b = 0`, then the least value of the expression `x^(2) + ax + b` is
View SolutionIf one root is the `n^("th")` power of the other root of the equation `x^(2) -ax + b = 0` then `b^((n)/(n+1))+b^((1)/(n+1))`=
View SolutionThe values of x for which the inequality `(8x^(2)+16x-51)/((2x-3)(x+4)) gt 3` holds, are
View SolutionIf `|(x^(2) + kx + 1)/(x^(2)+x+1)| lt 3` for real x, then k is in the interval
View Solution
PRACTICE EXERCISE questions and complete solutions for chapter QUADRATIC EQUATIONS & EXPRESSIONS of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12