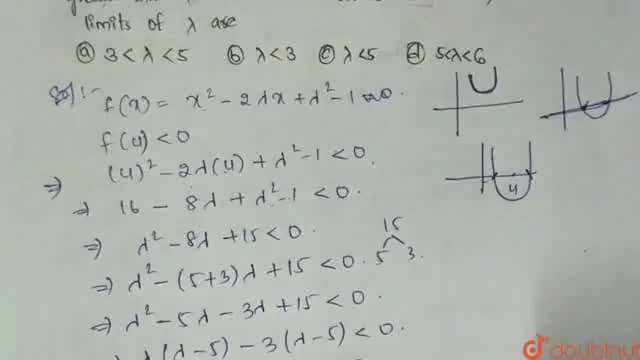Out of the two roots of x2−2λx+λ2−1=0, one is greater than 4 and the other root is less than 4, then the limits of λ areSolution in Telugu
3<λ<5
λ<3
λ<5
5<λ<6
The correct Answer is:A
Step by step video, text & image solution for Out of the two roots of x^(2)-2 lambda x + lambda^(2)-1= 0, one is greater than 4 and the other root is less than 4, then the limits of lambda are by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - QUADRATIC EQUATIONS & EXPRESSIONSEXERCISE - EXERCISE-II121videos
QUADRATIC EQUATIONS & EXPRESSIONS
- BOOK - AAKASH SERIESCHAPTER - PROBABILITYEXERCISE - Practise Exercise165videos
PROBABILITY
- BOOK - AAKASH SERIESCHAPTER - RANDOM VARIABLE EXERCISE - PRACTICE EXERCISE34videos
RANDOM VARIABLE
Similar Questions
IF α,β are real and α2,−β2 are the roots of a2x2+x+1−a2=0(A>1) then β2 =
01:13View SolutionThe probability that a non leap year will have 53 Wednesdays is
04:18View SolutionA random variable X ahs the following distribution
x1234P(X=x)c2c3c4c
The value of c is03:43View SolutionIf one roots of equation x^(2)-sqrt(3)x+lambda=0,lambda in R is sqrt(3)+2 then the other root is
04:27View SolutionThe value of lambda for which the equation 2x^(2)-2(2 lambda+1)x+lambda(lambda+1)=0 may have one root less than lambda and other root greater than lambda are given by
03:22View SolutionThe set of possible values of lambda for which x^(2)-(lambda^(2)-5 lambda+5)x+(2 lambda^(2)-3 lambda-4)=0 has roots whose sum and product are both less than 1 is
01:53View SolutionIf the two roots of the equation (lambda-1)(x^(2)+x+1)^(2)-(lambda+1)(x^(4)+x^(2)+1)=0 are real and distin then lambda lies in the interval
01:44View SolutionIf one root of f(x)=0 is less than 1 and the other is greater than 2, where f(x)=x^(2)-ax+4, then a cannot be
03:49View SolutionThe complete set of possible real values of à for which the equation x^(2)-(lambda^(2)+1)x-4 lambda^(2)=0 has roots whose simm and product both are greater than -1 is
04:03View Solutionयदि समीकरण 4x2−2x+(λ−4)=0 का एक मूल अन्य मूल का व्युत्क्रम हो, तो λ=
01:40View SolutionOut of the two roots of x2+(1−2λ)x+(λ2−λ−2)=0 one root is greater than 3 and the other root is less than 3 ,then the limits of λ are
03:01View SolutionIf λ= number of real root of x4+x2−2=0 then [cos2(1λ)] is equal to
03:21View SolutionOut of the two roots of x2−2λx+λ2−1=0 one is greater than 4 and the other root is less than 4, then the limits of λ are
02:17View SolutionThe values of a for which one root of the equation, x2+(2a+1)x+(a−2)=0 is greater than 1 and the other root less than zero, is
04:04View SolutionOut of the two roots of x2+(1−2λ)x+(λ2−λ−2)=0 one root is greater than 3 and the other root is less than 3, then the limits of λ are
05:08View Solution