Complete Solutions to PRACTICE EXERCISE of chapter CIRCLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CIRCLES |
| AAKASH SERIES | PRACTICE EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The circle with centre (1,1) and radius 1 is
View SolutionFor a circle two diameter are `x+y=3, x-y=1` then centre is
View SolutionCircle with centre (-1,2) and passing through origin is
View SolutionThe equation of the circle concentric with `x^(2)+y^(2)-6x+4y-3=0` and having radius 5 is
View SolutionThe equation of the circle concentric with `x^(2)+y^(2)-2x+8y-23=0` and passing through (2, 3) is
View SolutionFor the circle `x^(2)+y^(2)-4x+2y+c=0` radius is 4 then c=
View SolutionIf `A_(1),A_(2),A_(3)` be the areas of circles `x^(2)+y^(2)+4x+6y-19=0, x^(2)+y^(2)=9, x^(2)+y^(2)-4x-6y-12=0` respectively then `A_(1):A_(2):A_(3)`=
View SolutionThe equation of the circle with centre (2,3) and distance between (0,0) and (3,4) as radius is
View SolutionThe equation of the circle with radius 4 and centres as the midpoint of (1,4), (-3,2) is
View SolutionThe circle with centre (1,-3) and radius being the distance between the parallel lines `3x-4y-2=0, 3x-4y+8=0` is
View SolutionIf the area of the circle `x^(2)+y^(2)+4x+2y+k=0` is `5pi` square cms then k=
View SolutionIf (2,3) is an extremity of a diameter of the circle `x^(2)+y^(2)-5x-8y+21=0`, then the other extremity of the diameter is
View SolutionThe line `x/a+y/b=1` meets the axis of and y at A and B respectively and C is middle point of AB then
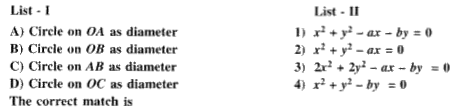
View SolutionEquation of circle with centre (-1,2) and passing through the centroid of triangle formed by (3,1),(2,-1) and (1,3) is
View SolutionThe centroid of an equilateral triangle is (0, 0) and the length of the altitude is 6. The equation of the circumcirele of the triangle is
View SolutionEquation of the circle with radius 10 and whose two diameters are `x+y=6 and x+2y=4" is "`
View SolutionIf a circle is inscribed in a square of side 10, so that the circle touches the four sides of the square internally then radius of the circle is
View SolutionShow that the equation of the circle which pass through the points (1,-2) and (4,-3) and whose centre lies on the line `3x+4y=7` is `15(x^(2)+y^(2))-94x+18y+55=0`
View SolutionIf the abscissae of points A, B are the roots of the equation `x^(2) + 2ax -b^(2) =0 ` and ordinates of A, B are roots of ` y^(2) + 2py -q^(2) =0 , ` then find the equation of the circle for which AB is a diameter.
View SolutionThe abscissae of two points A and B are the roots of the equation `x^(2)+2ax-b^(2)=0` and their ordinate are the roots fo the equations `y^(2)+2py-q^(2)=0` then the radius of the circle with AB as diameter is
View SolutionThe circle described on the line joining the points (0,1), (a,b) as diameter cuts the X-axis in points whose abscissae are roots of the equation
View SolutionThe equation of the circle passing through (3,0) and (0,4) and having the minimum radius is
View SolutionThe line `x/a+y/b=1` cuts the coordinate axes at a and B a line perpendicular to AB meets the axes in P and Q. The equation of the locus of the point of intersection of the lines AQ and BP is
View Solution`A(cos theta, sin theta), B (sin theta,- cos theta)` are two points then centroid of triangle formed by A,B and origin lies on a circle whose centre and radius are
View SolutionA circle of radius r passes through the origin and meets the axes at A and B. The locus of the centroid of `triangleOAB" is"`
View SolutionA rod AB of length 3 units moves vertically with its bottom B always an the circle `x^(2)+y^(2)=25` then the equation of the locus of A is
View SolutionA square is inscribed in the circle `x^(2)+y^(2)-2x+4y-93=0` with its sides are parallel to coordinate axes then vertices of square are
View SolutionAn equilateral triangle is inscribed in the circle `x^(2)+y^(2)=a^(2)`. The length of the side of the triangle is
View SolutionFind the equation of image circle of the circle `x^(2)+y^(2)-2x=0` in the line `x+y-2=0`
View SolutionThe shortest distance of (-5,4) to the circle `x^(2)+y^(2)-6x+4y-12=0` is
View SolutionThe circle passing through (0,0),(a,0), (0,b) is
View SolutionThe radius of the circle passing through the points (0,0),(0,3),(4,0) is
View SolutionIf a square of side 10 is inscribed in a circle then radius of the circle is
View SolutionIf the lines `lx+2y +3=0` and `2y+mx+4=0` cut the co-ordinate axes in concylic points then lm=
View SolutionIf the lines `2x-3y+7=0, 3x+ky+5=0` cut the coordinate axes in concyclie points then k=
View SolutionThe lines 2x+3y+19=0 and 9x+6y-17=0 cuts the coordinate axes in
View SolutionIf the points (3,0),(0,4),(0,0) and (k,4) are concylic then k=
View SolutionIf the lines `x-2y+3=0, 3x+ky+7=0` cut the coordinate axes in concylic points, then k=
View SolutionABCD is a rectangle wih sides AB=p, BC=q,. If AB and AD are taken negative directions of coordinate axes. then the equaton of the circumscribing the rectangle is
View SolutionFind the equation of the circle passing through the points
` (3,4) (3,2) ,(1,4) `
View SolutionThe sides of a square are `x=4, x=7, y=1, y=4`. Then the equation of the circumcircle of the square is
View SolutionThe points (2k, 3k), (1, 0), (0, 1) and (0, 0) lie on a circle for
View SolutionIf the 4 points made by intersection of lines `2x-y+1=0, x-2y+3=0` with the coordinate axes are concylic then centre of circle is
View SolutionThe lines `2x-5y+1=0` and `10x-4y-3=0` meets the coordinate axes in concylic points, then equation to the circle is
View SolutionThe power of (2,1) with respect to the circle `x^(2)+y^(2)+x=0` is
View SolutionIf the line passing through P=(8,3) meets the circle `S-=x^(2)+y^(2)-8x-10y+26=0` at A,B then PA.PB=
View SolutionA chord of length 8 units is at a distance of 4 uits from the centre of a circle then its radius is
View SolutionThe intercept made by the circle `x^(2)+y^(2)-4x-6y-3=0` on the line `x+y-3=0` is
View SolutionIf a line is drawn through a point A(3,4) to cut the circle `x^(2)+y^(2)=4` at P and Q then AP .AQ=
View SolutionThe condition that the chord a `x cos alpha +y sin alpha -p=0" of "x^(2)+y^(2)-a^(2)=0` subtend a right angle at the centre of the circle is
View SolutionThe equation of the cirlce with centre (0,0) and which cuts off a chord of length 4 units on `x+2y=5` is
View SolutionThe line `y=mx+c` intersects the circle `x^(2)+y^(2)=r^(2)` in two distinct points if
View SolutionIf a chord of the circle `x^(2)+y^(2)=16` makes equal intercepts of length a on the co ordinates axes then `|a|lt`
View SolutionThe pair of tangents from (2,1) to the circle `x^(2)+y^(2)=4` is
View SolutionThe equation of the tangent to the circle `x^(2)+y^(2)-4x+4y-2=0` at (1,1) is
View SolutionThe line `y=mx+c` touches `x^(2)+y^(2)=a^(2)hArr`
View SolutionThe radius of the circle which has the lines `x+y-1=0, x+y-9=0` as tangents is
View SolutionEquation of the tangent to the circle `x^(2)+y^(2)=3`, which is inclined at `60^(@)` with the x-axis is
View SolutionFind the equation of the normal to the circle ` x^(2) +y^(2) -4x -6y +11 0 ` at (3,2) Also find the other where the normal meets the circles.
View SolutionThe number of circles that touch all the 3 lines 2x+y=3, 4x-y=3, x+y=2 is
View SolutionP(-9,-1) is a point on the circle `x^2+y^(2)+4x+8y-38=0`. The equation to the tangent at the other end of the diameter thorugh P is
View SolutionThe line `x cos alpha+y sin alpha=p` touches the circle `x^(2)+y^(2)-2ax cos alpha-2ay sin alpha=0. then p=`
View SolutionThe equation of the tangent to the circle `x^(2)+y^(2)+4x-4y+4=0` which make equal intercepts on the positive coordinates, is
View SolutionThe tangent at (3,4), (4,-3) to the circle `x^(2)+y^(2)=25" are"`
View SolutionIf O is the origin OP, OQ are the tangent to the circle `x^(2)+y^(2)+2gx+2fy+c=0` then the circumcentre of the `triangleOPQ` is
View SolutionShow that `x + y + 1 = 0` touches the circle
`x^(2) + y^(2) -3x + 7y 14 = 0` and find its
point of contact.
View SolutionFind the equation of the circles which touch `2x-3y+1=0` at (1,1) and having radius `sqrt(13)`.
View SolutionIf the equatio of one tangent to the circle with centre (2,-1) from the origin is 3x+y=0, then the equation of the other tangent through the origin is
View SolutionThe normal of the circle `(x- 2)^(2)+ (y- 1)^(2) =16` which bisects the chord cut off by the line x-2y-3=0 is
View SolutionThe equation of the diameter of the circle `x^(2)+y^(2)+2x-4y=4=0` that is parallel to `3x+5y-4=0` is
View SolutionThe angle between the tangents to the circle with centre (4,5) drawn from P(-2,-3) is `120^(@)` then length of the tagent to the circle from P is
View SolutionThe locus of the point of intersection of two perpendicular tangents to the circle `x^(2)+y^(2)=a^(2)is`
View SolutionLocus of point of intersection of perpendicular tangents to the circle `x^(2)+y^(2)-4x-6y-1=0` is
View SolutionThe locus of the point of intersection of the perpendicular tangents to the circle `x^(2)+y^(2)=a^(2), x^(2)+y^(2)=b" is "`
View SolutionTangents from point P are drawn one of each of th circle `x^(2)+y^(2)-4x-8y+11=0` and `x^(2)+y^(2)-4x-8y+15=0` if the tangents are perpendicular then the locus o P is
View SolutionFrom any point on the circle `x^(2)+y^(2)=a^(2)` tangent are drawn to the circle `x^(2)+y^(2)=a^(2)sin^(2)theta`. The angle between them is
View SolutionThe tangents drawn from the origin `x^(2)+y^(2)-2rx-2hy+h^(2)=0` are per-pendicular if
View SolutionThe length of the tangent from a point on `x^(2)+y^(2)+8x+8y-4=0` to `2x^(2)+2y^(2)+16x+16y+1=0` is
View SolutionIf the length of the tangent from (f,g) to the circle `x^(2)+y^(2)=6` be twice the length of the tangent from the same point to the circle `x^(2)+y^(2)+3x+3y=0, ` then
View SolutionIf the square of the length of the tangents from a point P to the circles `x^(2)+y^(2)=a^(2), x^(2)+y^(2)=b^(2), x^(2)+y^(2)=c^(2)` are in A.P. then `a^(2),b^(2),c^(2)` are in
View SolutionIf the length of the tangent from (1,2) to the circle `x^(2)+y^2+x+y-4=0 and 3x^(2)+3y^(2)-x-y-lambda=0` are in the ratio 4:3 then `lambda=`
View SolutionA tangent to the circle `x^(2)+y^(2)=4` meets the coordinate axes at P and Q. The locus of midpoint of PQ is
View SolutionThe locus of the point of intersection of tangents to the circle `x=a cos theta, y=a sin theta` at points whose parametric angles differ by `pi//4` is
View SolutionThe circle with centre (2,3) touching x-axis has the radius equal to
View SolutionCircle touching y-axis and centre (3,2) is
View SolutionThe equation of the circle touching both the axes, lying in the third quadrant and having the radius 1 is
View SolutionThe x intercept of the circle `x^(2)+y^(2)+8x-9=0` is
View Solution`x^(2)+y^(2)-14x-10y+24=0` makes an
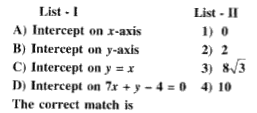
View SolutionIf `x^(2)+y^(2)+6x+2ky+25=0` to touch y-axis then k=
View SolutionA circle passes through (-2,4) and touches the y-axis at (0,2). Which one of the following equations can represent a diameter of this circle
View SolutionIf `I_(1),I_(2),I_(3)` are the intercept on x-axis, y-axis, y=x w.r.t `x^(2)+y^(2)-14x-10y+24=0` then
View SolutionIf a circle of radius 4 touches x-axis at (2,0) then its centre may be
View SolutionThe equation of the circle touching the coordinate axes the line `x+2=0` is
View SolutionTwo circles touching both the axes intersect at (3,-2) then the coordinates of their other point of intersection is
View SolutionIf two circles touching both the axes intersect at two points P and Q where P=(3,1) then PQ=
View SolutionThe equation of the circle passing through (2,1) and touching the coordinate axes is
View SolutionThe radius of the circle of least size that passes through (-2,1) and touches both axes is
View SolutionThe equation of the circle which touches both the axes and the line `4x+3y=6` in first quadrant and lies below it
View SolutionEquation of circle which touch X-axies at (3,0) and making Y-intercept of length 8 units is
View SolutionThe equation of the circles which touch the y-axis at the origin and the line 5x+12y-72=0 is
View Solution
PRACTICE EXERCISE questions and complete solutions for chapter CIRCLES of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS CIRCLES
- ADDITIONAL EXERCISE
- ADDITIONAL SOLVED EXAMPLES
- EXERCISE -I
- EXERCISE 1.1 ( LONG ANSWER QUESTIONS)
- EXERCISE 1.1 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.1 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE 1.2 ( LONG ANSWER QUESTIONS)
- EXERCISE 1.2 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.2 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE 1.3 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.3 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE 1.4 ( LONG ANSWER QUESTIONS)
- EXERCISE 1.4 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.4 ( VERY SHORT ANSWER QUESTIONS)
- EXERCISE II
- PRACTICE EXERCISE
- SOLVED EXAMPLES