Complete Solutions to EXERCISE II of chapter CIRCLES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CIRCLES |
| AAKASH SERIES | EXERCISE II |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The radius of the circle passing through (6,2) and the equation of two normals for the circle are `x+y=6` and `x+2y=4` is
View SolutionThe equation of the circle concentric with the circle `x^(2)+y^(2)-6x+12y+15=0` and of double its area is:
View SolutionIf the line 3x-2y + 6=0 meets X-axis and Y-axis respectively at A and B, then the equalion of the circle with radius AB and centre at A. is
View SolutionOrigin is the centre of a circle passing through the vertices of an equilateral triangie whose median is of length 3a then the equation of the circle is
View SolutionThe lines `2x-3y+5` and `3x-4y=7` are the diameters of a circle of area 154 sq. units. Then equation of circle is
View SolutionThe diameters of a circle pre along 2x+y-7=0 and x+3y- 11=0. Then, the equation of this circle, which also passes through (5,7) is:
View SolutionIf the two circles `x^(2)+y^(2)+2gx+c=0 and x^(2)+y^(2)-2fy-c=0` have equal radius then locus of (g,f) is
View SolutionCentre and radius of the circle with segment of the line `x+y=1` cut off by coordinate axes as diameter is
View SolutionThe line x+y=1 cuts the coordinate axes at P and Q and a line perpendicular to it meet the axes R and S. The equation to the locus of the intersection of lines PS and QR is
View SolutionThe equation of the circle passing through (2, 0) and (0, 4) and having the minimum radius is
View SolutionThe abscissae of two points A and B are the roots of the equation `x^(2)+2ax-b^(2)=0` and their ordinate are the roots fo the equations `y^(2)+2py-q^(2)=0` then the radius of the circle with AB as diameter is
View SolutionIf the circles described on the line joining the points (0,1) and `(alpha, beta)` as diameter cuts the axis of the points whose abscissae are the roots of the equation `x^(2)-5x+3=0" then "(alpha,beta)=`
View SolutionA rod AB of length 4 units moves horizontally with its left end A always on the circle `x^(2)+y^(2)-4x-18y-29=0` then the locus of the other end B is
View SolutionA line segment AM=a moves in the XOY plane such that AM is parallel to the X-axis. If A moves along the circle `x^(2)+y^(2)=a^(2)`, then the locus of M is
View SolutionLocus of centroid of the triangle whose vertices are ` (a cos t, a sin t ) , (b sin t - b cos t ) and (1, 0)` where ` t ` is a parameter, is
View SolutionA circle of constant radius 3k passes through (0,0) and cuts the axes in A and B then the locus of centroid of triangle OAB is
View SolutionA circle passes through origin and meets the axes at A and B so that (2,3) lies on `bar(AB)` then the locus of centroid of `DeltaOAB` is
View SolutionA rod PQ of length 2a sides with its ends on the axes the locus of the circumcentre of `triangleOPQ` is
View SolutionA line is at a distance c from origin and meets axes in A an dB. The locus of the centre of the circle passing through O,A,B ais
View SolutionA right angled isosceles triangle is inscribed in the circle `x^(2)+y^(2)-4x-2y-=0` then length of the side of the triangle is
View SolutionIf an equilateral triangle is inscribed in the circle `x^(2)+y^(2)-6x-4y+5=0` then its side is
View SolutionThe locus of the foot of the perpendicular drawn from orign to a variable line passing through fixed point (2,3) is a circle whose diameter is
View SolutionA square is inscribed in the circle`x^(2)+y^(2)-4x+6y-5=0` whose sides are parallel to co-ordinate axes then vetices of square are
View SolutionA square is inscribed in the circel `x^(2)+y^(2)-2x+7y-8=0` whose diagonals are parallel to axes and a vertex in the first quadrant is A then OA is
View SolutionThe length of the tangent drawn to the circle `x^(2)+y^(2)-2x+4y-11=0` from the point (1,3) is
View SolutionIf `(m_(1),1//m_(1)), i=1,2,3,4` are concyclic points, then the value of `m_(1)m_(2)m_(3)m_(4)" is"`
View SolutionThe equation of the image of the circle `x^(2)+y^(2)-6x-4y+12=0` by the line mirror x+y-1=0 is
View SolutionThe area bounded by circles `x^(2)+y^(2)=r^(2), r=1,2` and rays given by`2x^(2)-3xy-2y^(2)=0(hgt0)` is
View SolutionThe shortest distance from (-2,14) to the circle `x^(2)+y^(2)-6x-4y-12=0` is
View SolutionThe longest distance from (-3,2) to the circle
View SolutionIf the line `y=2x+c` is a tangent to the circle `x^(2)+y^(2)=5` then a value of c is
View SolutionThe sum of the minimum and maximum distances of the point (4,-3) to the circlex^2 +y^2+4x-10y-7=0
View SolutionIf the lines `3x-4y+4=0` and `6x-8y-7=0` are tangents to a circle, then the radius of the circle is
View SolutionThe nearest point on the circle `x^(2)+y^(2)-6x+4y-12=0` from (-5,4) is
View SolutionThe least distance of the line 8x-4y+73=0 from the circle `16x^(2)+16y^(2)+48x-8y-43=0`
View SolutionIf `d_(1)` and `d_(2)` are the longest the shortest distance of (-7,2) from any point `(alpha, beta)` on the curve whose equation is `x^(2)+y^(2)-10x-14y=51` then G.M. of `d_(1)` and `d_(2)` is
View SolutionEquation of circle passing through `(1,sqrt(3)), (1,-sqrt(3))` and `(3,-sqrt(3))` is
View SolutionThe equation of the circle of radius 3 that lies in 4th quadrant and touching the lines `x=0, y=0` is
View SolutionIf the points (2,0) (0,1), (4,0) and (0,a) are concylic then a=
View SolutionIf `O=(0,0),A=(1,0)` and `B=(1/2,(sqrt(3))/2)` then centre of circle for which the lines OA, OB and AB are tangents is
View SolutionThe circle passing through (5,-5),(1,7),(-7,1) is
View SolutionABCD is a square with side a. If AB and AD are taken as positive coordinate axes then equation of circle circumscribing the square is
View SolutionCentre of circle passing through A(0,1), B(2,3), C(-2,5) is
View SolutionCentre of the circle circumscribed in a rectangle formed by the lines `x^(2)-8x+12=0` and `y^(2)-14y+40=0` is
View SolutionIf the lines `2x+3y+1=0, 6x+4y+1=0` intersect the co-ordinate axes in 4 points, then the circle passing through the points is
View SolutionTwo rods of legths a and b slide along coordinate axes. Such that their ends are concylic. Locus of the centre of the circle is
View SolutionIf a line through P(-2,3) meets the circle `x^(2)+y^(2)-4x+2y+k=0` at A and B such that PA.PB=31 then the radius of the circles is
View SolutionThe locus of centre of a circle which passes through the origin and cuts off a length of 4 units from the line `x=3` is
View SolutionEquation of circle with centre (3,-1) and which cuts off a chord of length 6 on the line `2x-5y+18=0` is
View SolutionIf the line `3x-4y=lamda` cuts the circle `x^(2)+y^(2)-4x-8y-5=0` in two points then limits of `lamda` are
View SolutionIf a chord of the circle `x^(2)+y^(2)=8` makes equal intercepts of length a on the coordinate axes, then `|a| lt `
View SolutionIf the chord `y=mx+1` of the circle `x^(2)+y^(2)=1` subtends an angle of measure `45^(@)` at the major segment of the circle then m=
View SolutionThe triangle PQR is incribed in the circle `x^(2)+y^(2)=25`.If `Q=(3,4)` and R=(-4,3) then `/_QPR=`
View SolutionThe radius of circle having centre at (2,1) and whose on of the chord is diameter of the circle `x^(2)+y^(2)-2x-6y+6=0` is
View SolutionThe locus of th point (l,m). If the line lx+my=1 touches the circle `x^(2)+y^(2)=a^(2)` is
View SolutionEquation of the tangent to the circle `x^(2)+y^(2)-2x+4y-4=0` which is parallel to the line `3x+4y-1=0` is
View SolutionLocus of point of intersection of tangents to the circle `x^(2)+y^(2)=a^(2)` which makes complimentary angle with X axis is
View SolutionThe slope m of a tangent through the point (7,1) to the circle `x^(2)+y^2=25` satisfies the equation.
View SolutionThe tangents at (5,12) and (12,-5) to the circle `x^(2)+y^(2)=169` are
View SolutionTangents AB and AC are drawn to the circle`x^(2)+y^(2)-2x+4y+1=0` from A(0,1) then equation of circle passing through A,B and C is
View SolutionThe angle between the tangents to the circle with centre (4,5) drawn from P(-2,-3) is `120^(@)` then length of the tagent to the circle from P is
View SolutionAngle between tangents drawn from a points P to circle `x^(2)+y^(2)-4x-8y+8=0` is `60^(@)` then length of chord of contact of P is
View SolutionLocus of the point of intersection of tangents to the circle `x^(2)+y^(2)+2x+4y-1=0` which include an angle of `60^(2)` is
View SolutionThe angle between a pair of tangents drawn from a point P to the circle `x^(2)+y^(2)+4x-6y+9sin^(2)alpha+13 cos^(2)alpha=0" is "2alpha`. The equation of the locus of the point P is
View SolutionLocus of the point of intersection of perpendicular tangents to the circles `x^(2)+y^(2)=10` is
View SolutionLocus of point of intersection of perpendicular tangents to the circle `x^(2)+y^(2)-4x-6y-1=0` is
View SolutionLocus of the point of intersection of perpendicular tangents drawn one of each of the circles `x^(2)+y^(2)=8` and `x^(2)+y^(2)=12` is
View SolutionLocus of the points of intersection of perpendicular tangents drawn one to each of the circles `x^(2)+y^(2)-4x+6y-37=0, x^(2)+y^(2)-4x+6y-37=0, x^(2)+y^(2)-4x+6y-20=0` is
View SolutionThe condition that the pair of tangents drawn from origin to circle
`x^(2)+y^(2)+2gx+2fy+c=0` may be at right angles is
View SolutionIf two tangents are drawn from a point on `x^(2)+y^(2)=16` to the circle `x^(2)+y^(2)=8` then the angle between the tangents is
View SolutionFrom any point on the circle `x^(2)+y^(2)+2gx+2fy+c=0` tangents are drawn to the circle `x^(2)+y^(2)+2gx+2fy+c sin^(2) alpha +(g^(2)+f) cos^(2) alpha=0`. The angle between the tangents is
View SolutionAssertion (A): The director circle of `x^(2)+y^(20=4` is `x^(2)+y^(2)=`
Reason(R): The angle between the tangents from any point on `x^(2)+y^(2)=8` to `x^(2)+y^(2)=4` is `(pi)/2`
The correct answer is
View SolutionThe equation of the circle withcentre at (4,3) and touching the line `5x-12y-10=0` is
View SolutionNumebr of circles touching all the lines `x+y-1=0, x-y=1=0` and `y+1=0` are
View SolutionThe number of circles that touch all the straight lines x + y = 4, x - y = -2 and y = 2, is
View SolutionThe number of circles that touches all the three lines x+y-1=0, x-y-1=0 and y+1=0 is
View SolutionThe number of circles that touch all the 3 lines 2x+y=3, 4x-y=3, x+y=2 is
View SolutionNumber of circles touching all the lines `x+4h+1=0, 2x+3y+3=0` and `x-6y+3=0` is
View SolutionThe line y=x is a tangent at (0,0) to a circle of radius is 1, then centre of the circle is
View SolutionIf y=3x is a tangent to a circle with centre (1,1) then the other tangent drawn through (0,0) to the circle is
View SolutionIf the tangent at the point P on the circle `x^(2)+y^(2)+6x+6y=2` meet the line `5x-2y+6=0` at a point Q on y-axis then PQ=
View SolutionIf theline y=x touches the circle `x^(2)+y^(2)+2gx+2fy+c=0` at P where `OP=6sqrt2` then c=
View SolutionThe length of the tangent from a point on the circle `x^(2)+y^(2)+4x-6y-12=0` to the circle `x^(2)+y^(2)+4x-6y+4=0` is
View SolutionIf the length of the tangent from (h,k) to the circle `x^(2)+y^2=16` is twice the length of the tangent from the same point to the circle `x^(2)+y^(2)+2x+2y=0`, then
View SolutionThe locus of the points from which the lengths of the tangents to the two circles `x^(2)+y^(2)+4x+3=0, x^(2)+y^(2)-6x+5=0` are in the ratio 2:3 is a circle with centre
View SolutionThe tangent at any point to the circle `x^(2)+y^(2)=r^(2)` meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is
View SolutionThe tangents to `x^(2)+y^(2)=a^(2)` having inclinations `alpha and beta` intersect at P. If `cot alpha+cot beta=0`, then the locus of P is
View SolutionThe locus of the middle points of portions of the tangents to the circle `x^(2)+y^(2)=a^(2)` terminated by the axes is
View SolutionObserve the lists:
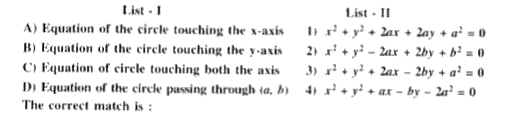
View SolutionIf a circle of radius 2 touches X-axis at (1,0) then its centre may be
View SolutionThe circle passing through (1,-2) and touching the axis of x at (3,0) also passes through the point:
View SolutionEquation of the tangents to the circle at the point (1,-1) whose centre is the point of intersection of the straight lines x-y=1 and 2x+y=3 is
View SolutionEquation of circles which touch both the axes and also the line `x=k(kgt0)` is
View SolutionCentres of circles touching both the axes and also the line `3x+4y-12=0` is
View SolutionThe radius of the larger circle lying in the first quadrant and touching the line 4x + 3y - 12 = 0 and the coordinate axes is
View SolutionThe equation of the circles which touch the x-axis at the origin and the line 4x-3y+24=0
View SolutionIf two circles touching both the axes are passing through (2,3) then length of their common chord is
View SolutionThe radius of the circle having maximum size passing through (2,4) and touching both the coordinate axes is
View SolutionConsider a family of circles which are passing through the point (-1,1) and are tangent to x-axis. If (h,k) are the co-ordinates of the centre of the circles, then the set of values of k is given by the internal.
View SolutionThe locus of centre of the circle touching x-axis nad the line `y=x` is
View Solution
EXERCISE II questions and complete solutions for chapter CIRCLES of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS CIRCLES
- ADDITIONAL EXERCISE
- ADDITIONAL SOLVED EXAMPLES
- EXERCISE -I
- EXERCISE 1.1 ( LONG ANSWER QUESTIONS)
- EXERCISE 1.1 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.1 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE 1.2 ( LONG ANSWER QUESTIONS)
- EXERCISE 1.2 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.2 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE 1.3 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.3 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE 1.4 ( LONG ANSWER QUESTIONS)
- EXERCISE 1.4 ( SHORT ANSWER QUESTIONS)
- EXERCISE 1.4 ( VERY SHORT ANSWER QUESTIONS)
- EXERCISE II
- PRACTICE EXERCISE
- SOLVED EXAMPLES