Complete Solutions to PRACTICE EXERCISE of chapter BINOMIAL THEOREM of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | BINOMIAL THEOREM |
| AAKASH SERIES | PRACTICE EXERCISE |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
The middle term in the expansion of `(x + 1/x)^(2n)` is
View SolutionIf the first three terms in the binomial expansion of `(1+bx)^n` in ascending powers of x are 1,6x and `16x^2` respectively then b + n =
View SolutionIf the first three terms in the expansion of `(1 -ax)^n` where n is a positive integer are 1,-4x and `7x^2` respectively then a =
View SolutionIn the expansion of `((x^2)/(2) - (2)/(x^2))^8`, the third term from the last is
View SolutionThe third term in the expansion of `(1/x + x ^[log_10 x])^5` is `10^6 `then x =
View SolutionThe numerically greatest term in the expansion `(5x - 6y)^14` when x = 2/5, y = 1/2 is
View SolutionThe no. of terms in `(x + sqrt(x^2 - 1))^6 + (x -sqrt(x^2 - 1))^6`
View SolutionNo. of distinct terms in `(x + y - z)^16` is
View SolutionNo. of distinct terms in `(a+b+c+d)^n , n in N` is
View SolutionIf the coefficient of `(2r + 4)^(th)` term and `(r - 2)^(th)` term in the expansion of `(1 + x)^18` are equal then find r.
View SolutionThe number of integral terms in the expansion of `(sqrt2 + root(4)(3))^100` is
View SolutionThe term independent of x in the expansion of `(x^2-(1)/(x))^6` is
View SolutionIf 5th term of the expansion `(root(3)(x) - 1/x)^n` is independent of x then n =
View SolutionTerm independent of x in `(1+4x)^p (1+(1)/(4x) )^q` is :
View SolutionTerm independent of x in `(x - 1/x)^4 (x + 1/x)^3` is
View SolutionThe sum of the binomial coefficients of the 3rd, 4th terms from the beginning and from the end of `(a+ x)^n` is 440 then n =
View SolutionIf the sum of odd terms and the sum of even terms in the expansion of `(x+a)^n` are p and q respectively then `p^2+q^2=`
View SolutionIf the sum of odd terms and the sum of even terms in `(x + a)^n` are p and q respectively then 4pq =
View SolutionIf A and B are coefficients of `x^(n)` in the expansion of `(1+x)^(2n)` and `(1+x)^(2n-1)` respectively, then find the value of `(A)/(B)`.
View SolutionThe coefficient of `x^(-17)` in `(x^4 - (1)/(x^3))^15` is
View SolutionThe coefficient of x in `(x^2 + a/x)^5` is 270 then a =
View SolutionIf the 21st and 22nd terms in the expansion `(1+x)^44` are equal then x =
View SolutionIf the coefficients of 2nd, 3rd, 4th terms of `(1+x)^n` are in A.P. then `n=`
View SolutionIf the coefficients of 2nd , 3rd and 4th terms of the expansion of `(1+x)^(2n)` are in A.P. then the value of `2n^2 -9n + 7` is
View SolutionIf the coefficients of 3rd, 4th , 5th terms in `(1+x)^(2n)` are A.P. then `4n^2 -26n + 40` =
View SolutionIf the coefficients of r,(r +1 ),(r+2) terms in `(1+x)^14` are in A.P. then r =
View SolutionIf three successive coefficients in `(1+x)^n` are 6,15,20 then n =
View SolutionIf `a_1,a_2,a_3,a_4` are the coefficients of 2nd, 3rd, 4th and 5th terms of `(1+x)^n` respectively then `(a_1)/(a_1+a_2) , (a_2)/(a_2+a_3),(a_3)/(a_3+a_4)` are in
View SolutionIf a,b,c,d are conseentive binomial coefficients of `(1+x)^n` then `(a+b)/(a), (b+c)/(b), (c+d)/(c )` are is
View SolutionCoefficient of `x^5` in `(1+x +x^2 +x^3)^10` is
View SolutionThe coefficient of `x^4` in the expansion of `(1+x-2x^2)^7` is
View SolutionBinomial coefficients which are in decreasing order are
View SolutionCoefficient of `x^3` in `1+(1+x) +(1 +x)^2 +…..+(1+x)^n` is
View SolutionSum of the coefficients of `(1+2x-4x^2)^(2003)`
View SolutionSum of coefficients of terms of even powers of x in `(1 + x + x^2 + x^3)^5` is
View SolutionSum of coefficients of terms of odd powers of in `(1+x - x^2 -x^3)^8`is
View SolutionIf `(1+x -2x^2)^8 =1 -a_1x + a_2x^2+……+a_16x^16, ` then `a_2+a_4+a_6+……+a_16` =
View SolutionIf `(1+x-2x^2)^8 = 1 + a_1x + a_2x^2 + ……+ a_16 x^16`, then `a_1 +a_3 + a_5 + ……+a_15 = `
View Solution`(1+x)^25 = sum_(r = 0)^(25) C_r x^r` then `C_1 - C_3 + C_5 - C_7 + ……-C_25 = `
View SolutionThe sum of the coefficients in the expansion of `(1+x-3x^2)^(171)` is
View SolutionIf the sum of all the binomial coefficients in `(x+y)^n` is 512 , then the greatest binomial coefficient is
View SolutionThe coefficient of `x^(-n)` in `(1+x)^n (1+(1)/(x))^n` is
View SolutionIf n is a positive integer then `2^(4n) - 15n - 1` is divisible by
View SolutionSmaller of `(19^10 + 20^10)` and `21^10` is
View Solution`9^11 + 11^9` is divisible by
View SolutionIntegral part of `(8 + 3sqrt7)^n` is
View SolutionIf `n = (sqrt2 +1)^6`. Then the integer just greater than n is
View Solution`1.C_0 + 3.C_1+ 3^2.C_2+….+3^n.C_n = `
View Solution` C_0 + (C_1)/(2) + (C_2)/(2^2) + (C_3)/(2^3)+…..+(C_n)/(2^n)=`
View Solution`""^11C_0 + ""^11C_1 + ""^11C_2 + ……+ ""^11C_5 = `
View Solution`C_0^2 + C_1^2 + C_2^2 - ………-C_15^2` =
View Solution`1/2.""^10C_0 -""^10C_1 +2.""^10C_2 - 2^2.""^10C_3+…..+2^9. ""^10C_10 = `
View Solution`""^(2n +1)C_0^2 -""^(2n+1)C_1^2 + ""^(2n+1)C_2^2 -…….- ""^(2n+1)C_(2n+1)^2` =
View SolutionProve that following
i) `2.C_(0)+5.C_(1)+8.C_(2)+…..+(3n+2)C_(n)=(3n+4).2^(n-1)`
View Solution`""^20C_0 + ""^20C_1 + ""^20C_2+…….+""^20C_10 = `
View Solution`C_1 + 2. C_2 + 3. C_3 + …... + n. C_n=`
View SolutionIf `a_r` is the coefficient of `x^r` in the expansion of `(1+x)^n` then `a_1/a_0 + 2.a_2/a_1 + 3.a_3/a_2 + …..+n.(a_n)/(a_(n-1))` =
View SolutionIf `(1+x)^n = C_0 + C_1 x+ C_2 x^2 + ….....+ C_n x^n, ` then `C_0+2. C_1 +3. C_2 +….+(n+1) . C_n=`
View Solution`1.""^20C_1 - 2.""^20C_2 + 3.""^20C_3 - …..-20.""^20C_20 = `
View Solution`(1+x+x^2 + ……+x^p)^n = a_0 + a_1x + a_2 x^2 + ….+a_(np) x^(np) rArr a_1 + 2a_2 + 3a_3 + ……+np .a_(np) =`
View Solution`C_1 + 4.C_2 +7.C_3 +…….+(3n-2).C_n= `
View Solution`sum_(r=1)^(n) (-1)^(r-1) ""^nC_r(a - r) = `
View Solution`2.C_0 + (2^2)/(2).C_1 + (2^3)/(3).C_2 + ……+(2^11)/(11).C_10 = `
View Solution`""^11C_0^2 - ""^11C_1^2 + ""^11C_2^2 - ""^11C_3^2 + ……- "^11C_11^2 = `
View Solution`(C_0)/(1) + (C_2)/(3) + (C_4)/(5) + ……+(C_16)/(17) = `
View Solution`(C_1)/(2) + (C_3)/(4) + …….+(C_15)/(16)= `
View SolutionThe coefficient of `x^3` in `(1-4x)^(1//2)` is
View SolutionThe range of x for which the expansion of `(1-3/x)^(-3//4)` is valid is
View SolutionThe range of x of which the expansion of `(2-3x^2)^(-11/2)`is valid is
View SolutionThe fifth term of `(1 - (2x)/(3))^(3//4)` is
View SolutionFor `|x| lt 1`, the `(r + 1)^(th)` term in the expansion of `sqrt(1 - x)` is
View SolutionThe general term of `(2a - 3b)^(-1//2)` is
View SolutionIn the expansion of `(1+x+x^2+x^3+…..oo)^3, ` coefficient of `x^3` is
View SolutionIn the expansion of `(1-2x+3x^2 -4x^3+…."to")^4` coefficient of `x^2` is
View SolutionThe coefficient of `x^24` in `(1+3x+6x^2 + 10x^3 + ……oo)^(2//3)` is
View SolutionThe coefficient of `x^10` in `(1-2x + 3x^2)/(1-x)` is
View SolutionThe coefficient of `x^9` in the expansion of `(1-5x)/(1+x)` is
View SolutionThe coefficient of `x^4` in the expansion of `((1 -3x)^2)/((1 - 2x))` is
View SolutionFor `|x| lt 1`, the coefficient of `x^r` in the expansion of `((1+x)^2)/((1-x)^3)` is
View SolutionIf `x = 1 + 3a + 6a^2 + 10 a^3 + ……" to " oo` terms `|a| lt 1, y = 1+4a+10a^2 + 20a^3 + ….." to " oo` terms, `|a| lt 1`, then x:y
View SolutionProve that : If `|x|` is so small that `x^(2)` and higher powers of x may be neglected, then find an approximate value of
View SolutionIf |x| is so small that all terms containing `x^2` and higher powers of x can be neglected , then the approximate value of `((3 - 5x)^(1//2))/((5 - 3x)^2), ` where `x = (1)/(sqrt363)` , is
View SolutionIf `x = (1*3)/(3*6)+(1*3*5)/(3*6*9)+(1*3*5*7)/(3*6*9*12)+. . . ` to infinite terms, then `9x^(2) + 24 x = `
View Solution`1-(1)/(5)+(1.4)/(5.10) - (1.5.7)/(5.10.15)+…..=`
View Solution`1+(1)/(2). (3)/(5) + (1.3)/(2.4) . (9)/(25)+(1.3.5)/(2.4.6).(27)/(125)+…...oo=`
View Solution`1+(1)/(4) + (1.3)/(4.8) + (1.3.5)/(4.8.12)+…...=`
View SolutionIf `x=(1)/(5)+(1.3)/(5.10)+(1.3.5)/(5.10.15)+….oo` then find `3x^(2)+6x.`
View Solution`2 + (5)/(2!3) + (5.7)/(3!3^2) + (5.7.9)/(4!3^2) + …..oo = `
View SolutionProve that : Find the sum of the infinite series
`1+(2)/(3).(1)/(2)+(2.5)/(3.6)((1)/(2))^(2)+(2.5.8)/(3.6.9)((1)/(2))^(3)+......oo`
View SolutionSho that `3/6 + (3.5)/(6.9) + (3.5.7)/(6.9.12)+ ……..oo 3 sqrt3 - 4`
View Solution`1 + 1/3 + (1.3)/(1.2) .(1)/(3^2) + (1.3.5.)/(1.2.3).(1)/(3^3) + ……oo = `
View SolutionObserve the following statements :
Statement - I: The total number of terms in the expansion of `(x+y)^100 + (x - y)^100` after simplification is 51
Statement - II : If `""^43C_(r-6) = ""^43C_(r + 1)` then r = 12
Statement - III : The coefficient of `x^n` in `(1-x)^(-2)` is (n+1) .
Then the true statements are :
View SolutionLet l,m,n are the coefficients of `x^5` in
`(1+2x+3x^2+…..)^(-3//2), (1+x+x^2 +x^3+….)^2, (1+x)^5`
Respectively then :
View SolutionMatch the following
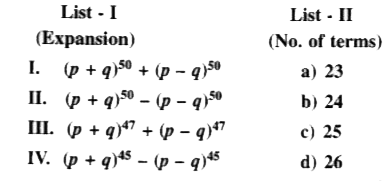
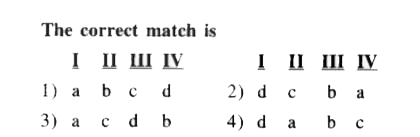
View SolutionMatch the following question

View Solution
PRACTICE EXERCISE questions and complete solutions for chapter BINOMIAL THEOREM of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS BINOMIAL THEOREM
- ADDITIONAL EXERCISE
- ADDITIONAL SOLVED EXAMPLES
- EXAMPLE
- EXERCISE - 1.1 (Level - 1)
- EXERCISE - 1.2 (Level - 1)
- EXERCISE - 1.3 (Level - 1)
- EXERCISE - 1.4 (Level-2)
- EXERCISE - 3.1 ( LONG ANSWER QUESTIONS)
- EXERCISE - 3.1 ( SHORT ANSWER QUESTIONS)
- EXERCISE - 3.1 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE - 3.2 ( LONG ANSWER QUESTIONS)
- EXERCISE - 3.2 ( SHORT ANSWER QUESTIONS)
- EXERCISE - 3.3 (LONG ANSWER QUESTIONS)
- EXERCISE - 3.3 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE - I
- EXERCISE - II
- PRACTICE EXERCISE
- SOLVED EXAMPLES