Complete Solutions to EXERCISE - II of chapter BINOMIAL THEOREM of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | BINOMIAL THEOREM |
| AAKASH SERIES | EXERCISE - II |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
If `r^(th)` term is middle term in `(x^2 - (1)/(2x))^20` then `(r+ 3)^(th)` term is
View SolutionIf 'a' is the coefficient of the middle term in the expansion of `(1 + x)^(2n)` and b,c are the coefficients of two middle terms in the expansion of `(1 + x)^(2n -1)` then
View SolutionThe coefficient of the middle term in `(1 + alpha x)^4` and `(1 - alpha x)^6` is same then `alpha = `
View SolutionThe numerical value of middle terms in `(1 - 1/x)^n (1 - x)^n` is
View SolutionIf the middle term of `(1+x)^ (2n)` is `(1.3.5….(2n-1)k)/(n!)` then `k=`
View SolutionThe coefficient of the middle term in the expansion of `(1+x)^40` is
View SolutionIf the third term in the expansion of `(x + x log_10 x)^5` is `10^6` then x is
View SolutionIn the expansion of `(1 + x)^n` if the 2nd and 3rd terms are respectively a,b then x =
View Solution`(18^3+7^3+3.18. 7. 25)/(3^6 +6.243.2+15.81.4+20.27.8+15.9.16+6.3.32+64)=`
View SolutionThe expansion `[x+(x^3-1)^(1//2)]^5+[x-(x^3-1)^(1//2)]^5` is a polynomial of degree
View SolutionIf the ratio of the 7th term from the beginning to the 7th term from the end in the expansion of `(sqrt2+(1)/(sqrt3))^x` is `1/6`, then x is
View SolutionIf the sum of odd terms and the sum of even terms in `(x + a)^n` are p and q respectively then `p^2 - q^2 = `
View SolutionIn the expansion of `(root(5)(3) + root(7)(2))^24` , then rational term is
View SolutionThe sum of the rational terms in expansion of `(sqrt2+3^(1//5))^10` is
View SolutionThe number of rational terms in the binomial expansion of `(root(4)5+root(5)4)^(100)` is
View SolutionThe number of irrational terms in the expansion of `(root(5)(3) + root(3)(7))^36` is
View SolutionThe number integral terms in the expansion of `(sqrt3+root(8)(5))^256` is
View SolutionThe sum of the coefficient of `x^32 and x^-17` in `(x^4-(1)/(x^3))^15` is
View SolutionIf the coefficient of `x^7` in `(ax^2+(1)/(bx))^11` equals the coefficient of `x^-7` in `(ax-(1)/(bx^2))^11`, then a and b satisfy the relation
View SolutionThe term independent of x in `(2x^(1//2)-3x^(-1//3))^20`
View SolutionIf the absolute term (independent of x ) in the expansion of `(sqrtx-k//x^2)^10` is 405 then `k=`
View SolutionIf the 5th term is the term independent of x in the expansion of `(x^(2//3) + 1/x)^n` then n =
View SolutionIf a term independent of x is to exist in the expansion of `(x + (1)/(x^2))^n` then n must be
View SolutionThe term independent of x in the expansion of `(1 + x)^n (1 + 1/x)^n` is
View SolutionThe sum of the coefficient in the expansion of `(1 + x+x^2)^n` is
View SolutionThe sum of the binomial coefficients in the expansion of `((2x)/(3) + (3)/(2x^2))^n` is 64 then the term independent of x is
View SolutionThe two successive terms in the expansion `(1+x)^24` whose coeff's are in the ratio `4:1` are
View SolutionIf two consecutive terms in the expansion of `(x+a)^n` are equal to where n is a positive integer then `((n+1)a)/(x+a)` is
View SolutionThe coefficient of `x^53` in `sum_(r = 0)^(100) ""^100C_r (x - 3)^(100 - r) .2^r` is
View SolutionLet `n in N` . If `(1 + x)^n = a_0 + a_1 x + a_2x^2+…. + a_nx^n` and `a_(n-3), a_(n-2) , a_(n-1) `are in A.P then
Statement - I ` : a_1, a_2, a_3` are in A.P.
Statement -II : n = 7
The true statements are :
View SolutionIf the coefficient of rth term and `(r+1)th` term in the expansion of `(1+x)^20` are in the ration `1:2`, then `r=`
View SolutionIf the coefficients of `r^(th) , (r + 1)^(th)` and `(r + 2)^(th)` terms in the binomial expansion of `(1 + y)^m` are in A.P. then m and r satisfy the equation
View SolutionIf the coefficients of three consecutive terms in the expansion of `(1+x)^n` are 45, 120 and 210 then the value of n is
View SolutionThe coefficient of `x^n` in expansion of `(1+x) (1-x)^n` is
View SolutionThe coefficient of `x^11` in the expansion of `(1- 2x + 3x^2) (1 + x)^11 ` is
View SolutionThe coefficient of `x^5` in the expansion of `(x^2 - x - 2)^5` is
View SolutionThe coefficient of `x^4` in `(1+x+x^2+x^3)^11` is
View SolutionCoefficient of `x^5` in `( 1+ x)^21 + (1 + x)^22 + …….+ (1 + x)^30` is
View SolutionCoefficient of `a^8b^6c^4` in `(a+b+c)^18` is
View SolutionThe coefficient of `x^9` in `(x - 1)(x - 4) ( x- 9) ……. ( x -100)` is
View SolutionThe term in `(x + y)^50` which is greatest in absolute value if `|x| = sqrt3 |y|` is
View SolutionThe greatest integer which divides the number `101^100 - 1 ` is
View Solution`9^7 + 7^9` is divisible by
View SolutionLarger of `99^50+100^50 and 101^50`
View SolutionThe remainder left out when `8^(2n) - 6(2)^( 2n+1)` is divided by 9 is
View SolutionIntegral part of 7 + 4sqrt3)^n` is `(n in N)`
View SolutionIntegral part of `(7 + 5sqrt2)^(2n+1) ` is `(n in N)`
View SolutionIf `(6 sqrt6+14)^(2n+1)=R and F=[R]`, where [R] denotes the greatest integer less than or equal to R thwn `RF=`
View SolutionThe integral part of `(sqrt2+1)^6` is
View Solution`""^(n) C_(r+1)+2""^(n)C_(r) +""^(n)C_(r-1)=`
View SolutionIf `C_k` is the coefficient of `x^k` in the expansion of `(1 + x)^2005` and if a,d are real numbers then `sum_(k = 0)^(2005) (a + kd).C_k` =
View SolutionThe sum of the series `""^20C_0 - ""^20C_1 + ""^20C_2 - ""^20C_3 +…….""^20C_10` is
View SolutionIf `S_(n) = underset (r=0) overset( n) sum (1) /(""^(n) C_(r))` and `T_(n) = underset(r=0) overset(n) sum (r )/(""^(n) C_(r))` then ` (t_(n))/(s_(n))` =
View Solution`C_0 - [C_1 -2.C_2+ 3.C_3-……..+(-1)^(n-1).n.C_n]` =
View Solution`C_0+4. C_1 + 7. C_2+…...(n+1)` terms =
View Solution`2. C_2 + 6. C_3 + 12. C_4 +….. + n (n-1) . C_n=`
View SolutionSum of last 8 coefficients in `(1 + x)^16` is
View Solution`C_0 + (C_1)/(2) (4) + (C_2)/(3) (16) + …………..+(C_n)/(n + 1) (2^(2n))`
View Solution`(1 +x)^15 = a_0 + a_1x +…..+a_15 x^15 rArr sum_(r = 1)^15 r (a_r)/(a_(r - 1)) = `
View SolutionThe value of `sum_(r = 1)^15 r^2 ((""^15C_r)/(""^15C_(r - 1)) )` of is equal to
View SolutionIf `a_k` is the coefficient of `x^k` in the expansion of `(1 +x+x^2)^n` for k = 0,1,2,……….,2n then `a_1 +2a_2 + 3a_3 + ………+2n.a_(2n) =`
View SolutionFind the sum of the following
`(""^(15)C_(1))/(""^(15)C_(0))+2(""^(15)C_(2))/(""^(15)C_(1))+3(""^(15)C_(3))/(""^(15)C_(2))+......+15(""^(15)C_(15))/(""^(15)C_(14))`
View SolutionIf `a_0, a_1 , a_2 …..a_n` are binomial coefficients then `(1 + a_1/a_0)(1 +a_2/a_1) …………….(1 + (a_n)/(a_(n-1)) ) = `
View Solution`((C_0 + C_1)(C_1 + C_2)(C_2 + C_3)………(C_(n-1) + C_n) )/(C_0C_1C_2…C_n)`
View SolutionIf `(1+x)(1+x+x^2)(1+x+x^2+x^3)……(1+x+x^2+……+x^(n-1))` = `a_0 + a_1x + a_2x^2 +…….+a_m x^m ` then `a_0 +a_1 + …..+ a_m = `
View SolutionIf `(1 -x + x^2)^n = a_0 +a_1x + a_2x^2+….+a_(2n)x^(2n)` then `a_0 + a_2 +a_4 + …….+a_(2n) = `
View SolutionIf `(1)/(1!(n-1)!) + (1)/(3!(n-3)!) + (1)/(5!(n-5)!) +…. = `
View Solution`C_0 + C_1 + 2.C_2(3) + 3.C_3(3^2)+ 4.C_4(3^3) + ……+n.C_n 3^(n-1) = `
View Solution`(1 + x+x^2)^8 = a_0 + a_1x +…….+a_16 x^16` then `a_0 - a_2 + a_4 - a_6 + ……..+a_16 = `
View SolutionIf `a_r` is the coefficient `x^r` in the expansion of `(1+x+x^2)^n` then `a_1 - 2a_2 + 3a_3 -…..-2na_(2n) = `
View SolutionIf `(1+2x +3x^2)^10 = a_0 +a_1x +a_2x^2 + ……+a_20x^20` then `a_2/a_1` =
View Solution`""^15C_2 + 2.""^15C_3 + 3. ""^15C_4 + …..+ 14.""^15C_15 = `
View Solution`""^20C_10.""^15C_0 + ""^20C_9.""^15C_1 + ""^20C_8.""^15C_2 + …..+""^20C_0.""^15C_10 = `
View Solution`""^10C_1 . ""^9C_5 + ""^10C_2. ""^9C_4 + ""^10C_3. ""^9C_3 + ""^10C_4. ""^9C_2 + ""^10C_5. ""^9C_1 + ""^10C_6 = ""^19C_6 + x ` then x =
View Solution`sum_(r=1)^(10) r. (""^nC_r)/(""^nC_(r-1)) = `
View Solution`sum_(r = 0)^(n-1) (C_r)/(C_r + C_(r+1)) = `
View SolutionThe sum of the coefficients in the binomial expansion of `(1/x + 2x)^n` is equal to 6561. The constant term in the expansion is
View SolutionIf `(1)/((1 - 2x)(1 + 3x))` is to tbe expanded as a power series of x, then
View Solution`1 + ""^2C_1x + ""^3C_2 + ""^4C_3 x^3 + …..` to ` oo` terms can be summed up if
View SolutionIf `S_n` denotes the sum of first n natural number then `S_1 + S_2x + S_3 x^2 +……+S_n x^(n-1) + ……oo` terms =
View Solution`""^4C_1 + ""^5C_2.(1/2) + ""^6C_3.(1/2)^2+…..` to `oo` terms :
View SolutionIf `|x| lt 1` , then the coefficient of `x^n` in expansion of `(1+x+x^2 + x^3 +…….)^2` is
View SolutionIf the expansion in powers of x of the function `(1)/((1-ax)(1-bx))` is `a_(0)+a_(1)x+a_(2)x^(2)+a_(3)x^(3)+.....+a_(n)` then coefficient of `x^(n)` is
View SolutionThe coefficient of `x^24` in the expansion of `(1+x^2)^(12) (1+x^12)(1+x^24)` is
View SolutionIf `0 lt x lt 1`, the first negative term in the expansion of `(1+x)^(27//5)` is
View SolutionFind the coefficient of `x^(10)` in the expansion of `(1+2x)/((1-2x)^(2))`.
View SolutionThe first negative term in the expansion of `(1+x)^(3//4)` is
View SolutionIf `T_(r +1)` is the first negative term in the expansion of `(1+x)^(7//2)` then r =
View SolutionIf `x^3, x^4, x^5` …….can be neglected then `sqrt(x^2 + 16 ) - sqrt(x^2 + 9) = `
View SolutionIf 'c' is small in comparison with l then `((l)/(l+c))^(1//2) + ((l)/(l-c))^(1//2)` =
View SolutionIf x is numerically so small so that `x^2` and higher powers of x can be neglected , then `(1+(2x)/(3))^(3/2), (32 + 5x)^(-1/5)` is approximately equal to :
View SolutionIf x is small so that `x^2` and higher powers can be neglected, then the approximately value for `((1-2x)^(-1) (1-3x)^(-2))/((1-4x)^(-3))` is
View Solution`1+(2)/(4) + (2.5)/(4.8)+(2.5.8)/(4.8.12)+(2.5.8.11)/(4.8.12.16)+…..=`
View Solution`(3)/(4.8)+(3.5)/(4.8.12)+(3.5.7)/(4.8.12.16)+….=`
View SolutionObserve the following statements :
Statement -I : In the expansion of `(1+x)^50,` the sum of the coefficients of odd powers of x is `2^50` .
Statement -II : The coefficient of `x^4` in the expansion of `(x/2 - (3)/(x^2))^10` is equal to `504/259` .
Then the true statements are :
View SolutionThe following coefficients which are in increasing order are :
View SolutionObserve the following statements :
Statement - I : `1/2 . ""^10C_0 - ""^10C_1 + 2. ""^10C_2 - 2^2. ""^10C_3 + ……+ 2^9. ""^10C_10 = -1/2`
Statement - II : `""^20C_1 - 2(""^20C_2) + 3.(""^20C_3)-…..-20.(""^20C_20) = 0`
Then the false statements are :
View SolutionThe number of terms in the expansions of `(1+3x+3x^2+x^3)^6, (x+y-z)^16, (x^2 - 2 + (1)/(x^2))^25` are `n_1, n_2, n_3` then
View Solution`(1+x)^n = sum_(r = 0)^(n) C_r x^r` then match the following
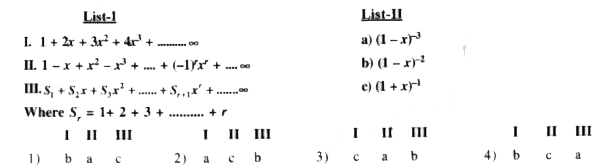
View Solution`(1+x)^n = sum_(r = 0)^(n) C_r x^r` then match the following
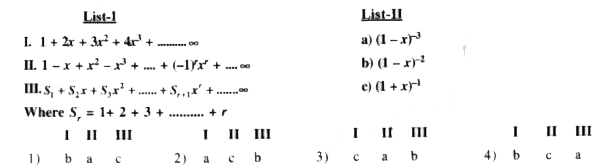
View Solution
EXERCISE - II questions and complete solutions for chapter BINOMIAL THEOREM of JEE (MAIN AND ADVANCED) MATHEMATICS of Class 12
All Exercises from AAKASH SERIES Class 12 MATHS BINOMIAL THEOREM
- ADDITIONAL EXERCISE
- ADDITIONAL SOLVED EXAMPLES
- EXAMPLE
- EXERCISE - 1.1 (Level - 1)
- EXERCISE - 1.2 (Level - 1)
- EXERCISE - 1.3 (Level - 1)
- EXERCISE - 1.4 (Level-2)
- EXERCISE - 3.1 ( LONG ANSWER QUESTIONS)
- EXERCISE - 3.1 ( SHORT ANSWER QUESTIONS)
- EXERCISE - 3.1 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE - 3.2 ( LONG ANSWER QUESTIONS)
- EXERCISE - 3.2 ( SHORT ANSWER QUESTIONS)
- EXERCISE - 3.3 (LONG ANSWER QUESTIONS)
- EXERCISE - 3.3 (VERY SHORT ANSWER QUESTIONS)
- EXERCISE - I
- EXERCISE - II
- PRACTICE EXERCISE
- SOLVED EXAMPLES