Complete Solutions to NEET Cafe (Topicwise practice Questions) of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMODYNAMICS |
| MTG GUIDE | NEET Cafe (Topicwise practice Questions) |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
Zeroth law of thermodynamics is related to
View SolutionWhich of the following is not a state function ?
View SolutionWhich of the following is not a thermodyanmic coordinate ?
View SolutionThe first law of thermodynamics is concerned with conservation of
View Solution`gamma` represents the ratio of two specific heats of a gas. For a given mass of the gas, the change in internal energy when the volume expands from V to 3V to constant pressure P is
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300 K. The piston of A is free to move, while that of B is held fixed. The same amount of heat is given to the gas ineach cylinder. If the rise in temperature of the gas in A to 30 K, then the rise in temperature of the gas in B is
View SolutionIf a gas (γ=4/3) is heated at constant pressure then what percentage of total heat supplied is used of external work ?
View SolutionA sample of ideal gas `(gamma = 1.4)` is heated at constant pressure. If 100 J of heat is supplied to the gas the work done by the gas is
View SolutionWhen a system is taken from state I to state f along the path iaf, it is found that Q = 50 cal and W = 20 cal. Along the path ibf, Q = 36 cal. W along the path ibf is

View SolutionA gas under constant pressure of `4.5 xx 10^(5)` Pa when subjected to 800 kJ of heat, changes the volume from `0.5 m^(3)` to `2.0 m^(3)`. The change in internal energy of the gas is
View SolutionA system is taken from state A to state N along two different paths 1 and 2. The heat absorbed and work done by system along these two paths are `Q_(1)` and `Q_(2)`, and `W_(1)` and `W_(2)` respectively. Then
View SolutionFor a diatomic gas change in internal energy for unit change in temperature for constant pressure and constant volume is `Delta U_(1)` and `Delta U_(2)` respectively. The ratio of `Delta U_(1) : Delta U_(2)` is
View SolutionWhen a system is taken from stata a to state b along the path acb as shown in figure, 60 J of heat flows into the system and 30 J of work is done by the system. Along the path adb, if the work done by the system is 10 J, heat flow into the system is
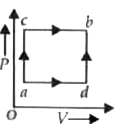
View SolutionHeat is supplied to a diatomic gas at constant pressure. The ratio of `Delta Q : Delta U : Delta W` is
View SolutionA system is taken from a given initial state to a given final state along various paths represented on a P-V diagram. The quantity that is independent of the path is
View SolutionWhich of the following is not a path function ?
View SolutionIf the amount of heat given to a system is 35 J and the amount of work done on the system is 15 J, then the change in internal energy of the system is
View SolutionIf a quantity of heat 1163.4 joule is suppled to one mole of nitrogen gas , at room temperature at constant pressure, then the rise in temperature is (Given `R = 8.31 J "mole"^(-1)K^(-1)`)
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_(P)//C_(V)` for gas is
View SolutionIn a cyclic process, work done by the system is
View SolutionOne mole of an ideal gas `(gamma = 1.4)` is adiabatically compressed so that its temperature rises from `27^(@)C` to `35^(@)C`. The change in the internal energy of the gas is (given R = 8.3 J/mole K)
View SolutionA thermodynamic process is shown in figure. In process ab, 600 J of heat is added, and in process bd 200 J of heat is added. The total heat added in process acd is
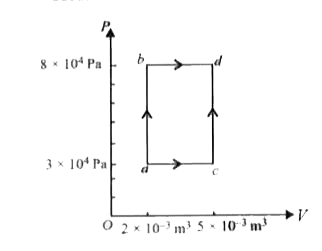
View SolutionPressure P, volume V and temperature T of a certain material are related by `P = alpha T^(2)//V` where `alpha` is contant. Work done by the material when temperature changes from `T_(0)` to `2T_(0)` and pressure remains constant is
View SolutionIn thermodynamic process which of the following statements is not true ?
View SolutionAn ideal gas is taken through the cycle `A rarr B rarr C rarr A`, as shown in figure. If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process `C rarr A` is
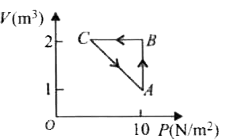
View SolutionWork done by the system in closed path ABCA, as shown in figure is
View SolutionThe relation between internal energy U, pressure P and volume V of a gas in an adiabatic process is
`U = a + bPV`
where a and b are positive constants. What is the value of `gamma` ?
View SolutionThree samples of the same gas A, B and C `(gamma = 3//2)` have equal volume initially. Now, the volume of each sample is doubled. For A, the process is adiabatic , for B, it is isobaric and for C, the process is isothermal. If the final pressures are equal for all the three samples, the ratio of their initial pressures is
View SolutionA one mole of an an ideal gas expands adiabatically at constant pressure such that its temperature `T prop (1)/(sqrt(V))`.
View SolutionA motor car type has a pressure of 2 atmosphere at `27^(@)C`. It suddenly burts. If `C_(P)//C_(V) = 1.4` for air, then the resulting temperature is
View SolutionTwo moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. The net work done by the gas is
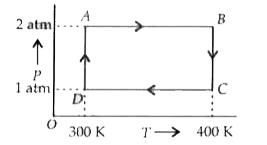
View SolutionTwo identical containers A and B with frinctionless pistons contain the same ideal gas at the same temperature and the same volume V. The mass of gas A is `m_(A)` and that of B is `m_(B)`. The gas in each cylinder is now allowed to expand in the pressure in A and B are found to be `Delta P` and `1.5 Delta P` respectively. Then
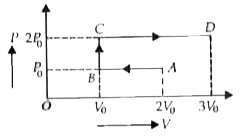
View SolutionA cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
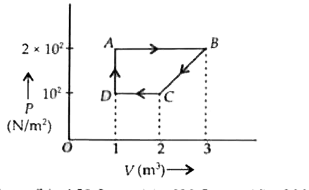
View SolutionOne mole of an ideal monatomic gas at temperature `T_(0)` expands slowly according to the law `(P)/(V)` = constant. If the final temperature is `2T_(0)`, heat supplied to the gas is
View SolutionThe P-V diagram of a gas undergoing a cyclic process (ABCDA) is shown in the graph, where P is in units of `Nm^(-2)` and V in `cm^(3)`. Identify the incorrect statement.
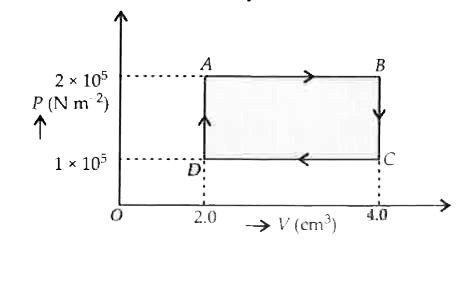
View Solution400 cc volume of a gas having `gamma = 5//2` is suddenly compressed to 100 cc. If the initial pressure is P, then the final pressure will be
View SolutionA monoatomic gas initially at `17^(@)C` is suddenly compressed to one eigth of its original volume. The temperature after compression is
View SolutionWhen a ideal gas with pressure P and volume V is compressed isothermally to one fourth of its volume, the pressure is `P_(1)`. When the same gas is compressed polytropically according to the equation `PV^(1.5)` = constant to one fourth of its initial volume, the pressure is `P_(2)`. THe ratio `(P_(1))/(P_(2))` is
View SolutionAn ideal gas at pressure P and volume V is expanded to volume 2V. Column I represents the thermodynamic process used during expansion. Column II represents the work done during processes in the random order.
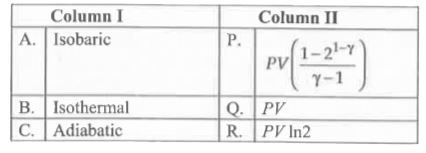
View SolutionA gas expands with temperature according to the relation `V = KT^(2//3)` where K is a constant. The work done by the gas when the temperature changes by 60 K is
View SolutionOne mole of an ideal gas is taken through a cyclic process as shown in the V-T diagram. Which of the following statements is true ?
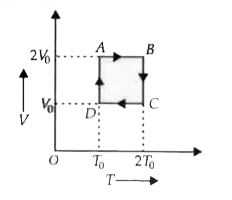
View SolutionPressure P, voluume V and temperature T for a certain gas are related by `P = (AT - BT^(2))/(V)` where A and B are constant. The work done by the gas as its temperature change from `T_(1)` to `T_(2)` with pressure remaining constant is
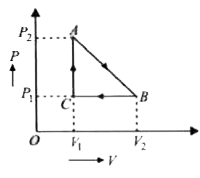
View SolutionA gas is expanded from volume `V_(0)` to `2V_(0)` under three different processes, as shown in the figure. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let `Delta U_(1), Delta U_(2)` and `DeltaU_(3)` be the change in internal energy of the gas in these three processes. Then
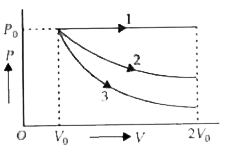
View SolutionTwo moles of helium gas are taken over the cycle ABCDA, as shown in below in P-T diagram. Assuming the gas to be ideal , the work done on the gas in taking it from A to B is
View SolutionThe temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure `P = aT^(-1)` where a is a constant. Then, the work done by the gas is
View SolutionP-V diagram of an ideal gas is as shown in figure. Work done by the gas in the process ABCD is
View SolutionFor a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume is `TV^(x)` = constant, where x is
View SolutionA polyatomic gas `(gamma = (4)/(3))` is compressed to `(1)/(8)^(th)` of its volume adiabatically. If its initially pressure is `P_(0)`. Its new pressure will be
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure `P_(1)`. The same gas is expanded adiabatically to a volume 2V, the final final pressure is `P_(A)`. In terms of the ratio of the two specific heats for the gas `gamma`, the ratio `P_(I)//P_(A)` is
View SolutionA given mass of gas is compressed isothermally untal its pressure is doubled. It is then allowed to expand adiabatically until its original volume is restore and its pressure is then found to be 0.75 of its initial pressure. The ratio of the specific heats of the gas is approximately
View SolutionA cyclic process for 1 mole of an ideal gas is shown in the V-T diagram. The work done in AB, BC and CA respectively are
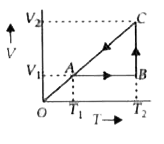
View SolutionStarting with the same initial conditions, an ideal gas expands from volume `V_(1)` to `V_(2)` in three different ways. The work done by the gas is `W_(1)` if the process is purely isothermal, `W_(2)` if purely isobaric and `W_(3)` is purely adiabatic. Then
View SolutionAn ideal gas is taken round a cyclic process represened by the triangle ABC drawn in order on a P-V diagram. The coordinates of A, B, C are (4,1), (2,4), (2,1) respectively. The work done in the complete cycle is
View Solution0.2 moles of an ideal gas is taken round the cycle ABC as shown in the figure. The path `B rarr C` is an adiabatic process `A rarr B` is an isochoric process and `C rarr A` is an isobaric process. The temperature at A and B are `T_(A) 300 K` and `T_(B) = 500 k` and pressure at A is 1 atm and volume at A is 4.91. The volume at C is
(given : `gamma = (C_(P))/(C_(V)) = (5)/(3), R = 8.205 xx 10^(-2) L "atm mol"^(-1) K^(-1), ((3)/(2))^(2//5) = 0.81`)
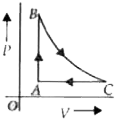
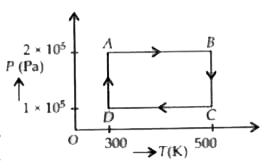
View SolutionA thermodynamic process is as shown in figure such that
`P_(A) = 3 xx 10^(4)Pa`,
`P_(B) = 8 xx 10^(4) Pa`,
`V_(A) = 2 xx 10^(-3) m^(3)`,
`V_(D) = 5 xx 10^(-3) m^(3)`
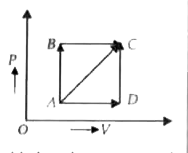
In procss AB, 600 J of heat is added to the system and in process BC, 200 J of heat is added to the system. The change in internal energy of the system in proess AC is
View SolutionThe thermodynamic process in which no work is done on or by the gas is
View SolutionThe work done by a gas is maximum when it expands
View SolutionAn ideal gas is taken around the cycle ABCA as shown in the P-V diagram.
The total work done by the gas during the cycle is
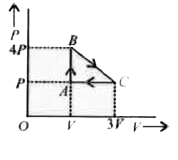
View SolutionNo heat flows between the system and surroundings. Then the thermdynamic process is
View SolutionThe volume of one mole of an ideal gas changes from V to 2V at temperature 300 K. If R is universal gas constant, then work done in this process is
View Solution"Heat cannot itself flow from a body at lower temperature to the body at higher temperature" is a statement or consequence of
View SolutionThe temperature `T_(1)` and `T_(2)` of heat reservoirs in the ideal Carnot engine are `1500^(@)C` and `500^(@)C` respectively. If `T_(1)` increases by `100^(@)C`, what will be the efficiency of the engine ?
View SolutionA Carnot engine operates with source at 500 K and sink at 375 K. Engine consumes 600 kcal of heat per cycle. The heat rejected to sink per cycle is
View SolutionA reversible engine converts one-sixth of the heat input into work. When the temperature of the sink is reduced by `62^(@)C`, the efficiency of the engine is doubled. The temperature of the source and sink are
View SolutionThe efficiency of a carnot engine working between temperature `T_(1)` and `T_(2)` is `eta`. It will be also `eta` if it works between temperatures
View SolutionAn engineer claims to have made an engine delivering 10 kW power with fuel consumption of 1g/sec. The calorific value of the fuel is 2 kcal/g. The claim of the engineer
View SolutionA Carnot engine operates with source at `127^(@)C` and sink at `27^(@)C`. If the source supplies 40 kJ of heat energy the work done by the engine is
View SolutionAn ideal gas hea engine operates in a Carnot cycle between `227^(@)C` and `127^(@)C`. It absorbs 6 kcal of heat at higher temperature. The amount of heat in kcal rejected to sink is
View SolutionThe efficiency of Carnot engine is 50% and temperature of sink is 500 K. If temperature of source is kept constant and its efficiency raised to 60%, then the required temperature of sink will be
View SolutionA heat engine has an efficiency `eta`. Temperature of source and sink are each decreased by 100 K. Then, the efficiency of the engine
View SolutionA steam engine delivers `5.4 xx 10^(8) j` of work per minute and absorbs `3.6 xx 10^(9) J` of heat per minute from its boiler. What is the efficiency of the engine ?
View SolutionA refrigerator is to maintain eatables kept inside at `9^(@)C`. The coefficient of performance of the refrigerator if room temperature is `36^(@)C`, is
View SolutionThe inside and outside temperature of a refrigerator are 273 K and 303 K respectively. Assuming that refrigerator cycle is reversible for every joule of work done, the heat delivered to the surroundings will be
View SolutionA Carnot engine takes `3 xx 10^(6)` cal of heat from a reservoir at `627^(@)C` and gives it to a sink `27^(@)C`. The work done by the engine is
View SolutionA Carnot engine will sink temperature at `17^(@)C` has 50% efficiency. By now much should its source temperature by changed to increase its efficiency to 60% ?
View SolutionA Carnot's reversible engine converts `(1)/(6)` of heat input into work. When the temperature of the sink is reduced by 62 K, the efficiency of Carnot's cycle becomes (1/3). The temperature of the source and the sink, in kelvin, are respectively
View SolutionA Carnot engine whose efficiency is 40%, receives heat at 500 K. If the efficiency is to be 50%, the source temperature for the same exhaust temperature is
View SolutionA Carnot cycle has the reversible processes in the following order :
View SolutionIf the energy input to a carnot engine is thrice the work it performs then, the fraction of energy rejected to the sink is
View SolutionTwo Carnot engines A and B are operated in series. The engine A receives heat from the source at temperature `T_(1)` and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature `T_(2)`. For what value of T the efficiencies of the two engines are equal.
View Solution
NEET Cafe (Topicwise practice Questions) questions and complete solutions for chapter THERMODYNAMICS of MTG GUIDE PHYSICS (HINGLISH) of Class 11