Complete Solutions to Illustration of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | THERMODYNAMICS |
| MTG GUIDE | Illustration |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
Calculate the work done.
(a) Along path AB (b) Along path BC
(c ) Along path CA
(d) For the whole cycle.
The indicator diagram, between P and V, is as shown.
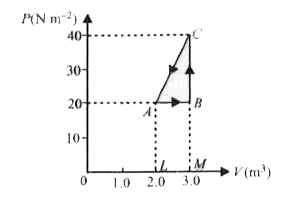
View SolutionIn the indicator diagram, we have
(a) Change in internal energy along ABC is 10 J.
(b) Work done along path AB = 20 J.
`U_(C ) = 5 J`.
(d) Heat absorbed by the system along path AD is 5J.
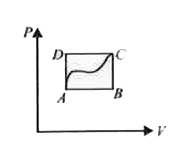
(i) Change in internal energy along the path CDA.
(ii) Heat given to the system along path ABC.
(iii) Value of `U_(A)`.
(iv) change in internal energy along AD.
View SolutionA certain mass of gas is carried from A to B, along three paths via ACB, ADB and AEB. Indicate the path along which the work done is
(a) Maximum
(b) Minimum.
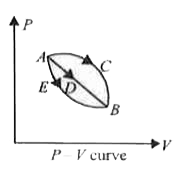
View SolutionThe P-V curves in two cases are shown as a smaller circle x and a bigger circle y, in the figure, Indicate whether the net work done is positive or negative.
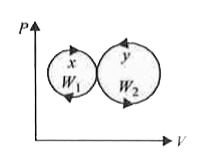
View SolutionIf heat given to a system is 6 kcal and work done is 6kj, then calculate the change in internal energy.
View SolutionTwo gram-moles of a gas are compressed isothermally at 273 K from `10 m^(3)` to `1m^(3)`. Calculate the work done during compression.
View SolutionWhich of the following is correct for the case of isothermal expansion of an ideal gas ?
View SolutionWhich of the following graphs correctly represents the variation of `beta = -((dV)/(dP))(1)/(V)` with P for an ideal gas at constant temperature ?
View SolutionThe pressure `P_(1)` and density `d_(1)` of a diatomic gas `(gamma = 7//5)` change to `P_(2)` and `d_(2)` during an adiabatic opertation. If `(d_(2))/(d_(1)) = 32`, find `(P_(2))/(P_(1))`.
View SolutionThe volume of air increases by 2% in its adiabatic expansion. Calculate the percentage decrease in pressure.
View SolutionTwo moles of an ideal monoatomic gas occupy a volume V at `27^(@)C`. The gas expands adiabatically to a volume 8V. Find the change in internal energy of the system.
[Given `C_(V) = (3R)/(2)J mol^(-1).^(@)C^(-1)`]
View SolutionTen moles of `N_(2)`, contained at constant pressure, is heated from `27^(@)C` to `527^(@)C`. Calculate the amount of heat required. R - 2 cal /(mol `xx .^(@)C`).
View SolutionThe pressure of a gas during an adiabatic operation, is found to be proportional to the cube of its absolute temperature. Calculate the ratio of specific heats of the gas.
View SolutionA monoatomic ideal gas, initially at temperature `T_(1)` is enclosed in a cylinder fitted with a frictionless piston. The gas is allowed to expand adiabatically to a temperature `T_(2)` by releasing the piston suddenly. If `L_(1)` and `L_(2)` are the lengths of the gas column. before and after expansion respectively, then `(T_(1))/(T_(2))` is given by
View SolutionA carnot engine maintains constant efficiency between 27 K and 527 K and between T K and 1054 K. Determine the unknown temperature.
View SolutionA Carnot's engine extract `1.5 xx 10^(3)` kilocalorie of heat from a reservoir at `627^(@)C` and exhaust it to a sink maintained at `27^(@)C`. How much work is performed by the engine ?
View SolutionA reversible heat engine converts one-sixth of heat, which it extracts from source, into work. When the temperature of the sink is reduce by `40^(@)C`, its efficiency is doubled. Find the temperature of source.
View SolutionFour engines are working between
Which one has maximum efficiency ?
View SolutionA refrigerator whose coefficient of performance is 5 extracts heat from the cooling compartment at the rate of 250 J per cycle. How mush electric energy is spend per cycle ? How much heat per cycle is discharged to the room ?
View SolutionThe coeffcient of performance of a refrigerator working between `10^(@)C` and `20^(@)C` is
View Solution
Illustration questions and complete solutions for chapter THERMODYNAMICS of MTG GUIDE PHYSICS (HINGLISH) of Class 11