Complete Solutions to COMPETITION FILE (JEE (Main) & Other State Boards for Engineering Entrance ) of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| MODERN PUBLICATION | COMPETITION FILE (JEE (Main) & Other State Boards for Engineering Entrance ) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Take the mean distance of the moon and the sun from the earth to be`0.4 xx 10^(6) km` and `150 xx 10^(6) km` respectively. Their masses are `8 xx 10^(22) kg` and `2 xx 10^(30) kg` respectively. The radius of the earth of is `6400 km`. Let `DeltaF_(1)`be the difference in the forces exerted by the moon at the nearest and farthest points on the earth and `DeltaF_(2)` be the difference in the force exerted b the sun at the nearest and farthest points on the earth. Then, the number closest to `(DeltaF_(1))/(DeltaF_(2))` is :
View SolutionThe relative uncertainty in the period of a satellite orbiting around the earth is `10^(-2)` . If the relative uncertainty in the radius of the orbit is negligible, the relative uncertainty in the mass of the earth is :
View SolutionThe height at which the acceleration due to gravity becomes `(g)/(9)` (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionSuppose that angular velocity of rotation of earth is increased. Then, as a consequence :
View SolutionIf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionThe energy required to take a satellite to a height ‘h’ above Earth surface (radius of Earth`=6.4xx10^3` km ) is `E_1` and kinetic energy required for the satellite to be in a circular orbit at this height is `E_2`. The value of h for which `E_1` and `E_2` are equal, is:
View SolutionA body of mass m is moving in a circular orbit of radius R about a planet of mass M. At some instant, it splits into two equal masses. The first mass moves in a circular orbit of radius `R/2`. And the other mass, in a circular orbit of radius `(3R)/(2)`. The difference between the final and initial total energies is :
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radiu `(R )/(2)` is removed as shown in the figure. Taking gravitational potential V = 0 at `r = oo`, the potential at the centre of the cavity thus formed is (G = gravitational constant)
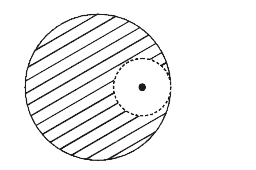
View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, `h lt lt R`). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth's gravitational field, is close to :(Neglect the effect of atmosphere.)
View SolutionThe value of acceleration due to gravity at earth's surface is `9.8 ms^(-2)`. The altitude above its surface at which the acceleration due to gravity decreases to , is close to: (radius of earth `= 6.4 xx 10^(6) m`)
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is `r_(2) - r_(1)`
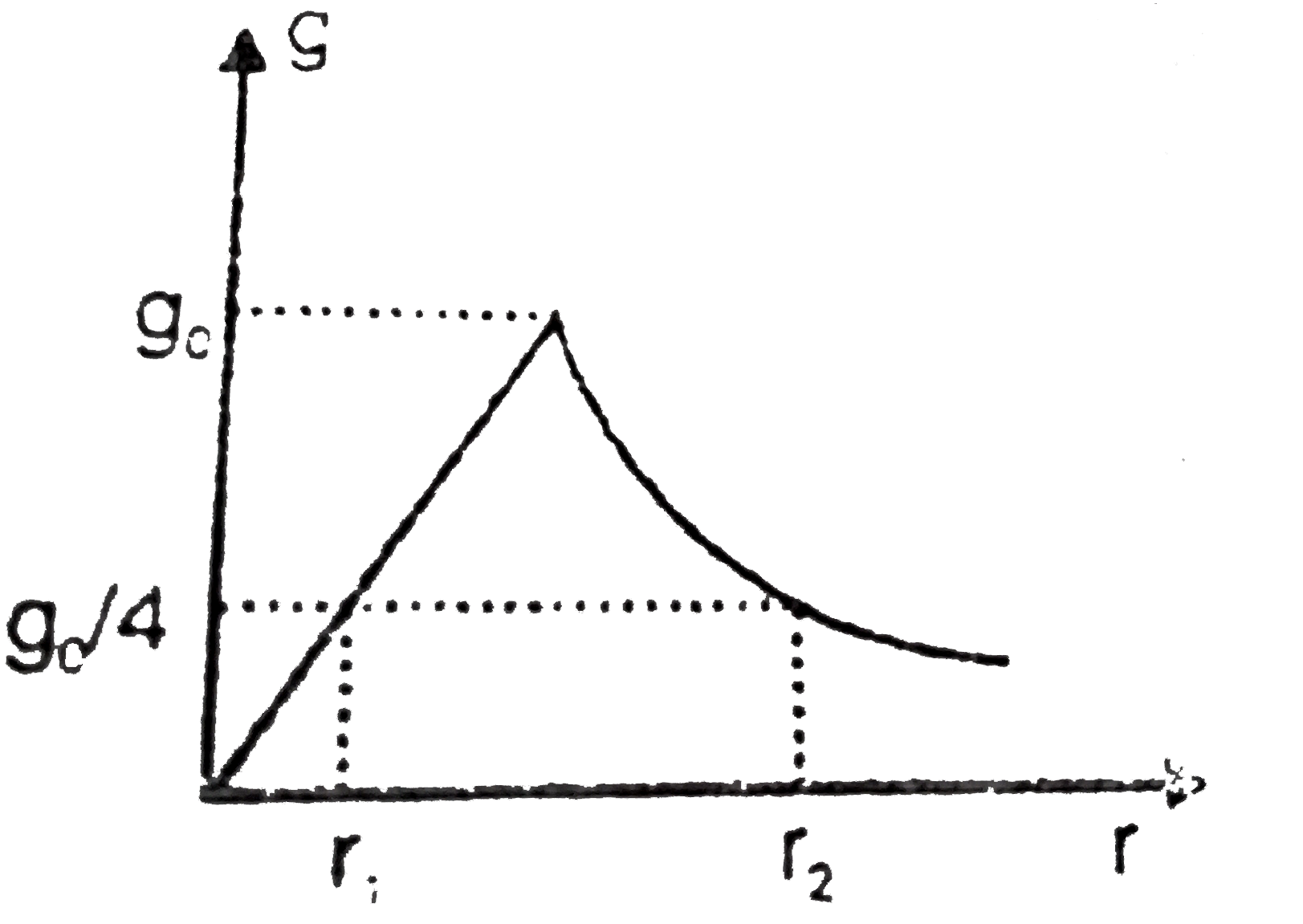
View SolutionIf the earth has no rotational motion, the weight of a person on the equation is W. Detrmine the speed with which the earth would have to rotate about its axis so that the person at the equator will weight `(3)/(4)` W. Radius of the earth is 6400 km and g = 10 `m//s^(2)`.
View SolutionThe mass density of a spherical body is given by `rho(r)=k/r` for `r le R` and `rho (r)=0`for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density `rho(r)=K/r^2`. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View Solution
COMPETITION FILE (JEE (Main) & Other State Boards for Engineering Entrance ) questions and complete solutions for chapter GRAVITATION of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS GRAVITATION
- A. Competition file (Objective Type questions) (Multiple Choice Questions(With one correct answer))
- Chapter Practice Test
- COMPETITION FILE (Integer Types questions)
- COMPETITION FILE ( (Objective Type questions) (Multiple Choice Questions(With one correct answer)))
- COMPETITION FILE ( Assertion Reasion Type Questions)
- COMPETITION FILE ( C. Multiple Choice Questions)
- COMPETITION FILE ( D (Multiple Choice Questions))
- COMPETITION FILE ( Jee (Advanced) for IIT Entrance)
- COMPETITION FILE (B.(Multipe Choice Questions from Competitive Examinations) AIPMT/NEET & Other State Boards for Medical Entrance)
- COMPETITION FILE (JEE (Main) & Other State Boards for Engineering Entrance )
- COMPETITION FILE (Matching Type Questions)
- COMPETITION FILE (Matrix Match Type Questions)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT FILE (Additional Exercises)
- NCERT FILE (Exemplar Problems (Objective Questions) (Multiple Choice questions) )
- NCERT FILE (TEXTBOOK EXERCISES)
- Practice Problems
- Revision Exercises (Additional questions)
- Revision Exercises (Fill in the blanks )
- Revision Exercises (Long Answer Questions)
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short answer type question)
- Revision Exercises (very short answer questions)
- Solved Example
- Tough & Tricky Problems