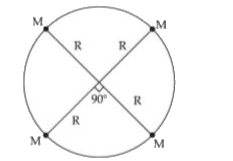
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:

$\frac{1}{2} \sqrt{\frac{G M}{R} (1 + 2 \sqrt{2})}$

$\sqrt{\frac{G M}{R}}$

$\sqrt{(2 \sqrt{2} \frac{G M}{R})}$

$\sqrt{\frac{G M}{R} (1 + 2 \sqrt{2})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Two particles each of mass M and equidistant from each other move along a circle of radius R under the action of their mutual gravitional attraction the speed of each particle is
A $\frac{\sqrt{G M}}{2 R}$
B $\frac{1}{2 R} \frac{\sqrt{1}}{G M}$
C $\frac{1}{2} \sqrt{G \frac{M}{R}}$
D $\frac{\sqrt{4 G M}}{R}$
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A $\sqrt{\frac{G M}{R}}$
B $\sqrt{2 \sqrt{2} \frac{G M}{R}}$
C $\sqrt{\frac{G M}{R} (1 + 2 \sqrt{2})}$
D $\frac{1}{2} \sqrt{\frac{G M}{R} (1 + 2 \sqrt{2})}$
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A $\frac{G m}{R}$
B $\sqrt{2 \sqrt{2} \frac{G M}{R}}$
C $\frac{\sqrt{G M}}{R} (2 \sqrt{2} + 1)$
D $\frac{\sqrt{G M}}{R} \frac{2 \sqrt{2} + 1}{4}$