Complete Solutions to SOLVED EXAMPLES of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| MODERN PUBLICATION | SOLVED EXAMPLES |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
A man carries a suitcase on head by applying a force of 20 N . He travels a horizontal a distance of 10 m and then climbs a vertical distance of 5 m . Calculate the total work done by him .
View SolutionA force `vec(F) = (2hat(i) - 3hat(j) +7hat(k))` N is applied on a particle which displaces it by `vec(S) = (4hat(i)+5hat(j) +hat(k))` . Find the work done on the particle .
View SolutionA cyclist comes to a skidding stop in `10m`. During this process, the force on the cycle due to the road is `200N` and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?
View SolutionTwo forces ` vec(F)_(1) = - hat(i) + 2 hat(j) - 3hat(k) and vec(F)_(2) = 2hat(i) - 4hat(j) +3hat(k)` act on a body and cause it to displace from point A(3,1,2) to `B (-4,-2,3)` . Calculate the total work done on the particle .
View SolutionA uniform rope of length 3 m and mass 1 kg is kept on a table such that 80 cm of its length hangs freely from the edge of the table . Calculate the work done in pulling the entire rope on the table .
View SolutionA man of weight 60 kg f is carrying a load of 20 kg of on his head . He moves a distance of 25 m up an incline of 1 in 12 . Calculate the work done by him .
View SolutionCalculate the kinetic energy acquired by a body of mass 5 kg initially at rest , when subjected to a force of 20 N , at the end of 8 s .
View SolutionA toy rocket having mass 0.2 has a small fuel of mass `0.04` kg which it burna out in 6 s. Starting from rest on a horizontal smooth track , it gets a speed of 40 m/s after the fuel is burnt out completey . What will be the approximate thrust of the rocket ? What is the energy content per unit mass of the fuel ? (Ignore the small mass variation of the rocket during fuel burning )
View SolutionA bullet of mass 20 g is fired with a velocity of 1000 m/s . After passing through a mud wall 1.5 m thick , its velocity decreases to 400 m/s . Calculate the average resistance offered by the mud wall .
View SolutionIt is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of `50.0ms^(-1)` (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionTwo identical bodies of mass 4 kg each are approaching each other with a speed of 3 m/s , on a frictionless horizontal surface . When the two bodies collide , they stick together and come to rest . Calculate the work done by the external forces and internal forces on the system of blocks .
View SolutionCalculate the % increase in kinetic energy of a body if its linear momentum increases by 50 % .
View SolutionA lady running on the road has kinetic energy that is half of that of girl . The girl's mass is half of the lady's mass. The lady increases her speed y m/s and then has the same energy as of girl . Calculate the original speeds of the lady and the girl .
View SolutionA block of mass `m=1kg` moving on a horizontal surface with speed `v_(i)=2ms^(-1)` enters a rough patch ranging from `x0.10m to x=2.01m`. The retarding force `F_(r)` on the block in this range ins inversely proportional to x over this range
`F_(r)=-(k)/(x) fo r 0.1 lt xlt 2.01m`
`=0` for `lt 0.1m` and `x gt 2.01m` where `k=0.5J`. What is the final K.E. and speed `v_(f)` of the block as it crosses the patch?
View SolutionA force `F = p+qx` acts on a particle in the X - direction , where p and q are constants . If the particle is displaced from x = a to x = b , find the work done by the force .
View SolutionA variable force as shown in the figure given below acts on a body and displaces it from point A to B . What is the amount of work dons ?

View SolutionA particle moves along Y - axis from y = 0 m under the influence of a force `F = (9+3y+5y)^(2)` N . Calculate the work done on the particle .
View SolutionA woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100N over a distance of 10m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50N. The total distance through which trunk has been moved is 20m. Plot the force applied by the woman and the frictional force, which is 50N against the distance. Calculat the work done by the two forces over 20m.
View SolutionA truck of mass 2000 kg climbs up hill of height 250 m . It then moves on a straight road on the top of hill with the speed of 20 m/s . Calculate the potential energy gained by the truck and its total mechanical energy when moving on the top of the hill .
View SolutionA bob of mass 2 kg hangs from a string of length 5 m . It swings from its rest position to one of the sides so that the string makes an angle of `60^(@)` with the vertical Calculate the gain in potential energy of the bob .
View SolutionA ball initally at rest is dropped from a height of 10 m . In strinking the ground , it loses 20 % of its kinetic energy . Calculate the height to which it bounces . Where does the lost kinetic energy go ?
View SolutionA round pebble is released from the point X inside a frictionless hemispherical ball as shown in the figure such that it just upto edge Y of the bowl . With what speed the pebble is released down inside the bowl ?
View SolutionA wooden bob of mass 1 kg is suspended from a string of length 1 m . It is struck by a bullet of mass 0.02 kg , moving with a speed of 300 m/s , such that the bullet gets embedded inside it . Calculate the maximum height up to which the bob will rise after the impact .
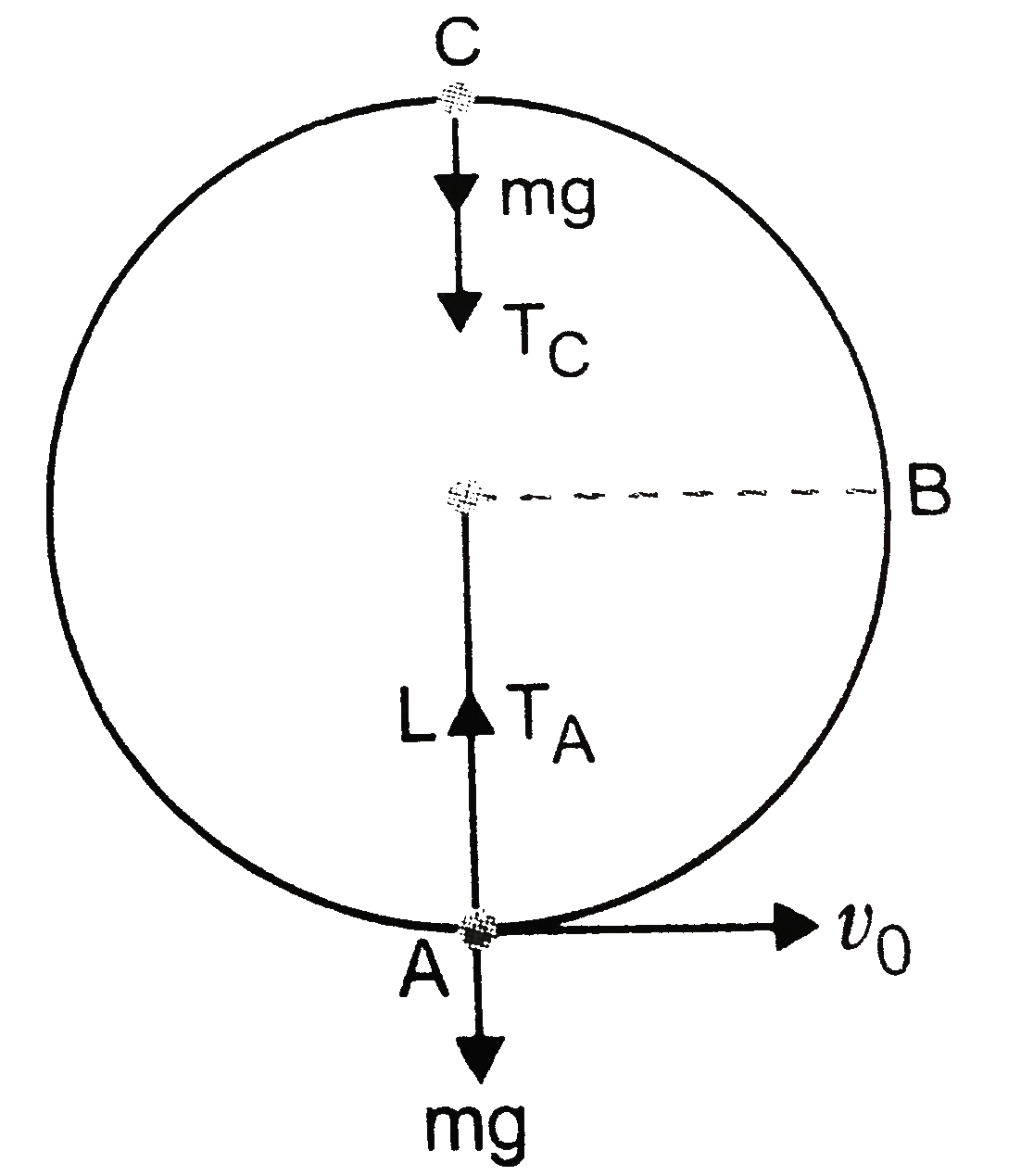
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
View SolutionWhen a steel wire is loaded with a weight of 3 kg , its length increases y 0.2 cm . Calculate the force constant of the wire and the work done in stretching the wire .
View SolutionTo simulate car accidents auto manufactures study the collisions of moving cars with mounted springs of different spring constants . Consider a typical simulation car of mass 1000 kg moving with a speed `18.0 " km h "^(-1)` on a smooth road and colliding `6.25 xx 10^(3) "Nm"^(-1)` . What is the maximum compression of the spring ?
View SolutionIn the figure shown below , a block of mass 4 kg is attached to a spring constant 24 N/m . The coefficient og friction `mu = 0.5` . If the system is initially at rest and a constant horizontal force of 50 N is applied on the block , then calculate its speed when it is moved through a distance of 0.6 m .

View SolutionGiven figure shows a massless platform kept on a light elastic spring attached to ground from one end .
A small particle of mass 0.2 kg is dropped on the paltform from a height of 0.26 m , which causes a compression of 0.01 m in the spring . Calculate the height from which the particle must be dropped in order to cause a compressin of 0.05 m .
View SolutionA body of mass 0.4 kg is tied to one end of a string and the other end of the string is tied to a small pivot on a vertical wall . Calculate the minimum speed of the body required at its lower most pint to avoid slacking of string at any point in its motion along the vertical circle of radius 1 m .
View SolutionA body of mass 0.6 mg kg is whirled in a vertical circle making 5 revolutions in one second . If the radius of the circle is 1.4 m , find the tension in the string , when the body is (i) at the lower most of the circle point , (ii) at the top of the circle .
View SolutionA bucket of water tied to one end of a rope of length 3 m is rotated in a vertical circle about the other end in such a way that water in it dows not spill . Calculate the minimum velocity of the bucket at which this happens .
View SolutionA stone of mass 0.4 kg is tied to a string and rotated in a vertical circle of radius 1.2 m . Calculate the speed of the stone for which the tension in the string is zero at the highest point of the circle . What is the tension at the lowest point in this case ?
View SolutionA fighter plane flying in the sky describes a vertical circle of radius 150 m when looping with a speed of 420 km/h . The weight of the pilot sitting inside it is 90 kg . With what force the pilot presses his seat when the plane is at the
(i) highest position of circle
(ii) lowest position of circle
View SolutionHow much mass is converted into energy per second in the sun if this power output is `3.6 xx10^(27)` W ?
View Solution400 kg of water is heated from `30^(@) C ` to `100^(@)C` . What will be the increase in mass of water ? Take specific heat of wateer ` = 4.2 xx10^(3) " J kg"^(-1).^(@)C^(-1)` .
View SolutionAn elevator in a building is designed to carry a load of 5000 kg throgh 10 floors . If height of each floor is 5 cm on an average and it takes 8 seconds to climb 10 floors , calculate the horse power of the lift .
View SolutionA car having mass 4000 kg is lifted up a distance of 60 m by a crane in 2 min . A second crane does the same job in 4 min . How much fuel is consumed by two cranes ? What is the power supplied by each crane ? Ignore power dissipation against friction .
View SolutionA motor of power 10 kW is used to pump water from a well 20 m deep . Calculate the efficiency of the motor if it pumps 200 kg of water every minute . Take `g = 10 m//s^(2)`
View SolutionAn elevator can carry a maximum load of `1800 kg` (elevator + passengers) is moving up with a constant speed of `2 ms^(-1)`. The friction force opposite the motion is `4000 N`.What is minimum power delivered by the motor to the elevator?
View SolutionA 25 m deep well contains water upto 15 m . An engine evacuates the well in 1.5 hrs . If the diameter of the well is 2 m ,calculate the power of the engine .
View SolutionTwo balls of masses 10 kg and 20 kg approach each other with velocities 30 m/s and 20 m/s respectively . Calculate their velocities after they undergo a perfectly eleastic collision .
View SolutionA truck of mass 1000 kg moving with a speed of 72 km/hr collides with a stationary truck of the same mass . After the collision , the trucks get stick together and move . Calculate their common speed after collision . Is it elastic or ineleastic collision ?
View SolutionIn a nuclear reactor, a neutron of high speed `(~~10^(7)ms^(-1))` must be slowed down to `10^(3)ms^(-1)` so that it can have a high probality of interacting with isotipe `_92U^(235)` and causing it to fission. Show that a neutron can lose most of its K.E. in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a fewe times the neutron mass. The material making up the light nuclei usually heavy water `(D_(2)O)` or graphite is called modertaor.
View SolutionA ball is dropped from a heght of 3.6 m and strikes a horizontal surface . It rebounds from the horizontal surface to height h . Calculate h , if coefficient of restitution is 0.6
View SolutionWhen a ball is dropped from a certain height h , it robounds from the ground , strikes again and rebounds again , a number of times before finally coming to rest . If the coefficient of restitution is e , find the height to which it robunds after `p^(th)` collision ..
View SolutionA spherical body moving with a speed of 10 m/s strikes another identical body at rest such that after collision , the direction of motion of each ball makes an angle of `15^(@)` with the original direction of motion .
Calculate the speed of each body after collision .
View SolutionConsider the collision depicted in Figure, to be between two billiard balls with equal masses `m_(1)=m_(2)`. The first ball is called the cue and the second ball is called the target. The billiard player wants to sink the target ball in a corner pocket, which is at an angle `theta_(2)=phi=37^(@)`. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain `theta_(1)=theta` .
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter WORK, ENERGY AND POWER of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS WORK, ENERGY AND POWER
- Chapter Practice Test
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level
- NCERT FILE (Exemplar Problems Objective Questions)
- NCERT FILE (NCERT Additional Exercise)
- NCERT FILE (NCERT Exemplar Problems (Short Answer Type Questions))
- NCERT FILE (NCERT Exemplar Problems (Very Short Answer Type Questions))
- NCERT FILE (NCERT Textbook Exercise)
- Objective Type Questions (A. Multiple Choice Questions)
- Objective Type Questions (Assertion Reason Type Questions)
- Objective Type Questions (B. Multiple Choice Questions)
- Objective Type Questions (C. Multiple Choice Questions)
- Objective Type Questions (D. Multiple Choice Questions)
- Objective Type Questions (Integer Type Questions)
- Objective Type Questions (JEE (Advanced) for IIT Entrance)
- Objective Type Questions (JEE (Main) & Other State Boards for Engineering Entrance)
- Objective Type Questions (Matrix Match Type Questions)
- PRACTICE PROBLEMS
- Revision Exercise (Additional Questions)
- Revision Exercise (Fill in the blanks)
- Revision Exercise (Long Answer Questions)
- Revision Exercise (Numerical Problems)
- Revision Exercise (Short Answer Questions)
- Revision Exercise (Very Short Answer Questions)
- SOLVED EXAMPLES
- Tough & Tricky (PROBLEMS)